Содержание
- 2. Цели урока Знать алгоритм решения задач методом «следов» и методом параллельного проецирования; Уметь решать задачи на
- 3. А А 1 в в 1 D D 1 С С 1 А А 1 в
- 4. А А 1 в в 1 D D 1 С С 1 А А 1 в
- 5. А А 1 в в 1 D D 1 С С 1 4. N M А
- 6. А А 1 в в 1 D D 1 С С 1 4. N M А
- 7. Отметка «5» - 10 баллов; Отметка «4» - 8-9 баллов; Отметка «3» - 6-7 баллов; Отметка
- 8. Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть точки данного многогранника. Сечением
- 9. Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть многоугольник, лежащий в секущей плоскости.
- 10. Две плоскости пересекаются по прямой (эта аксиома и дала названию метода – под «следом» понимается прямая
- 11. A B C D B1 C1 D1 M N K Выбираем точки М и N, принадлежащие
- 12. A B C D B1 C1 D1 M N K A1 E Теперь обращаем внимание, что
- 13. A B C D B1 C1 D1 M N K A1 E Точки Е и К
- 14. A B C D B1 C1 D1 M N K A1 E F Далее видим, что
- 15. A B C D B1 C1 D1 M N K A1 E F G Полученная точка
- 16. A B C D C1 D1 M N K A1 E F G H Остается соединить
- 17. Плоскость сечения может задаваться: 1) тремя точками, не лежащими на одной прямой; 2) прямой и точкой,
- 18. Данный метод построения сечений многогранников можно применять, если найдется хотя бы одна пара точек, лежащих в
- 19. Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то эти отрезки параллельны.
- 20. Пятиугольное сечение Построение: MN NK MP ||NK KH ||MN PH MNKHP- искомое сечение A B D
- 21. Шестиугольное сечение Построение: MN, NK MN∩AD=X XY ||NK XY∩AB=P XY∩BC=Q MP,PQ QH ||MN KH MNKHQP- искомое
- 22. Какие из данных сечений верны, а какие нет и почему? Ответ обоснуйте.
- 23. Какие из данных сечений верны, а какие нет и почему? Ответ обоснуйте.
- 24. A B D C A1 C1 D1 A B C D A1 D1 C1 B1 B1
- 26. Скачать презентацию























 Параллельные и перпендикулярные прямые - презентация по Геометрии
Параллельные и перпендикулярные прямые - презентация по Геометрии схема схема
схема схема Выполнил: Студент гр 916 Ковардинов Павел
Выполнил: Студент гр 916 Ковардинов Павел  Iran
Iran  «Прямоугольник»
«Прямоугольник» СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ Составитель: Дзюба Л.М. Учитель ГОУ ЦО 173 Г. Санкт-Петербург
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ Составитель: Дзюба Л.М. Учитель ГОУ ЦО 173 Г. Санкт-Петербург Тела вращения - презентация по Геометрии
Тела вращения - презентация по Геометрии Начальные геометрические сведения
Начальные геометрические сведения Симметрия. Осевая и центральная симметрии - презентация по Геометрии_
Симметрия. Осевая и центральная симметрии - презентация по Геометрии_ Длина окружности - презентация по Геометрии
Длина окружности - презентация по Геометрии Урок обобщающего повторения по теме «Теорема Пифагора» в 8 классе Учитель Ошкина Т.А.
Урок обобщающего повторения по теме «Теорема Пифагора» в 8 классе Учитель Ошкина Т.А.  Декартовы координаты
Декартовы координаты  Геометрия у меня в доме - презентация по Геометрии
Геометрия у меня в доме - презентация по Геометрии Виды треугольников
Виды треугольников  5класс
5класс 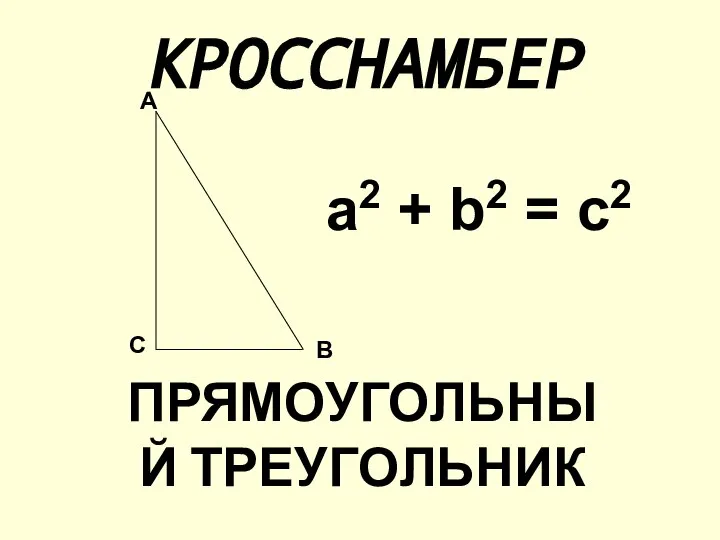 КРОССНАМБЕР ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
КРОССНАМБЕР ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК  Применение подобия к решению задач 8 класс.
Применение подобия к решению задач 8 класс. Тела вращения
Тела вращения Вписанный угол
Вписанный угол Перпендикуляр и наклонные
Перпендикуляр и наклонные Презентация по геометрии Первый признак равенства треугольников
Презентация по геометрии Первый признак равенства треугольников  Прямые. Скрещивающиеся - презентация по Геометрии_
Прямые. Скрещивающиеся - презентация по Геометрии_ Об аксиомах геометрии - презентация по Геометрии_
Об аксиомах геометрии - презентация по Геометрии_ Различные способы доказательства теоремы Пифагора По материалам Интернета исследование провела учитель математики МКОУ Букрее
Различные способы доказательства теоремы Пифагора По материалам Интернета исследование провела учитель математики МКОУ Букрее Виды соединений и их чертежи - презентация по Геометрии_
Виды соединений и их чертежи - презентация по Геометрии_ ТЕЛА ВРАЩЕНИЯ Самостоятельная работа
ТЕЛА ВРАЩЕНИЯ Самостоятельная работа Что мы знаем о параллельности - презентация по Геометрии
Что мы знаем о параллельности - презентация по Геометрии Площадь прямоугольника Ладанова И.В. – учитель математики МКОУ «Верх-Жилинская ООШ» Косихинский район Алтайский край
Площадь прямоугольника Ладанова И.В. – учитель математики МКОУ «Верх-Жилинская ООШ» Косихинский район Алтайский край