ТЕМА: Объемы тел Проект выполнили ученицы 11 «А»класса МОУ Алексеевской СОШ Плешакова Дарья и Щукова Ксения Работа выполнена под
Содержание
- 2. Содержание: История изучения объемов тел. История измерения объемов тел. Понятие объема. Свойства объемов тел. Объем куба.
- 3. История изучения объемов тел: Начало геометрии было положено в древности при решении чисто практических задач. Со
- 4. Архимед В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются правила для определения объема усеченной пирамиды, но
- 5. История измерения объемов тел: В Древнем Египте гробницы фараонов имели форму пирамид. В III тысячелетии до
- 6. Демокрит Согласно Архимеду, еще в V до н.э. Демокрит из Абдеры установил, что объем пирамиды равен
- 7. Евклид Полное доказательство этой теоремы дал Евдокс Книдский в IV до н.э.
- 8. Теоремы Евклида Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и
- 9. Понятие объема: Объем — это вместимость геометрического тела, т. е. части пространства, ограниченной одной или несколькими
- 10. Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами: равные тела
- 11. Свойства объемов тел: Объем тела есть неотрицательное число; Если геометрическое тело составлено из геометрических тел, не
- 12. Объем куба: V=a³
- 13. Объем прямоугольного параллелепипеда: Для того чтобы найти объем прямоугольного параллелепипеда с линейными размерами a, b, c
- 14. Примеры из жизни:
- 15. Объем прямой призмы: Объем прямой призмы равен произведению площади основания на высоту: V = SH .
- 16. Объем цилиндра: Данное тело имеет объем V, если существуют содержащие его простые тела и содержащиеся в
- 17. Примеры из жизни:
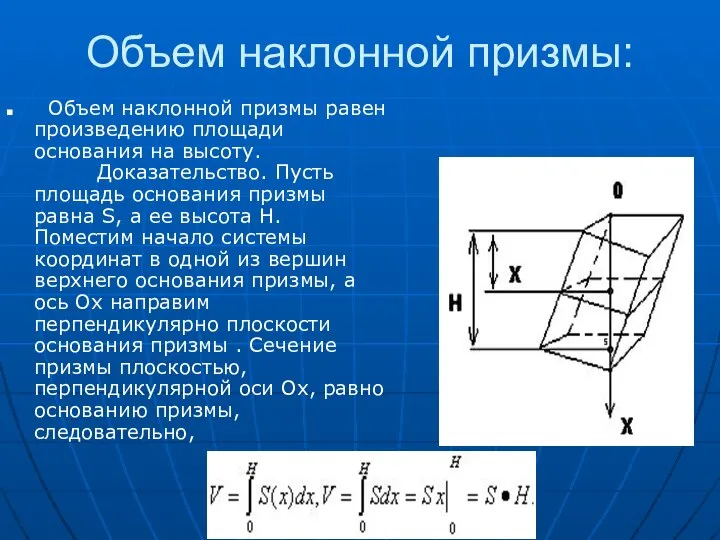
- 18. Объем наклонной призмы: Объем наклонной призмы равен произведению площади основания на высоту. Доказательство. Пусть площадь основания
- 19. Объем пирамиды: Объем любой пирамиды равен одной третьей произведения площади ее основания на высоту: V=1/3SH
- 20. Примеры из жизни:
- 21. Объем конуса: Объем конуса вычисляется по формуле где R — радиус основания конуса, H -- его
- 22. Примеры из жизни:
- 23. Применение: Формулы объемов тел широко применяются в строительстве
- 24. Объем цилиндра :V= ПR^2H Объем цилиндра :V= ПR^2H
- 25. V=1/3ПR^2H Объем конуса V=1/3ПR^2H Объем конуса Объем параллелепипеда V=SH
- 26. Вывод: 1.Объем куба равен кубу его ребра: V=a³ 2.Объем прямоугольного параллелепипеда равен произведению его измерений: V=abc.
- 27. Источники информации: Учебник геометрии 11класс. Авторы:Л.С.Атанасян,В.Ф.Бутузов, С.Б.Кадомцев. http://e-science.ru/ http://www.freesession.ru/ http://festival.1september.ru/
- 28. СПАСИБО ЗА ВНИМАНИЕ!!!
- 30. Скачать презентацию


























 Теорема Пифагора и способы ее доказательства - презентация по Геометрии
Теорема Пифагора и способы ее доказательства - презентация по Геометрии Зарождение геометрии Геометрия возникла в результате практической деятельности людей: нужно было сооружать жилища, храмы, прок
Зарождение геометрии Геометрия возникла в результате практической деятельности людей: нужно было сооружать жилища, храмы, прок Медианы треугольника Свойства медиан
Медианы треугольника Свойства медиан Объем прямой призмы
Объем прямой призмы «Число, положение и комбинаторика – три взаимно пересекающиеся, но различные сферы мысли, к которым можно отнести все математичес
«Число, положение и комбинаторика – три взаимно пересекающиеся, но различные сферы мысли, к которым можно отнести все математичес Урок математики в 4-м классе по теме "Виды треугольников" Выполнила: Лихачёва Любовь Николаевна  
Урок математики в 4-м классе по теме "Виды треугольников" Выполнила: Лихачёва Любовь Николаевна   ГБОУ СОШ №593 с углубленным изучением английского языка Невского района Санкт-Петербурга Презентация по математике на тему:
ГБОУ СОШ №593 с углубленным изучением английского языка Невского района Санкт-Петербурга Презентация по математике на тему:  История симметрии
История симметрии Доклад на тему: «Вневписанная окружность» Номинация: математика Выполнили: Коляда Валентина Афонина Екатерина ученицы 9м класс
Доклад на тему: «Вневписанная окружность» Номинация: математика Выполнили: Коляда Валентина Афонина Екатерина ученицы 9м класс Начальные геометрические сведения Учитель математики МКОУ « Москаленский лицей» Бадюк Ольга Ярославна
Начальные геометрические сведения Учитель математики МКОУ « Москаленский лицей» Бадюк Ольга Ярославна  Признаки параллельности двух прямых - презентация по Геометрии
Признаки параллельности двух прямых - презентация по Геометрии Работу выполнили:Шабалина Мария и Ганджалян Жанна Преподаватель геометрии: Хайбрахманова Г.Ф.
Работу выполнили:Шабалина Мария и Ганджалян Жанна Преподаватель геометрии: Хайбрахманова Г.Ф. Урок №21 Построение сечений параллелепипеда
Урок №21 Построение сечений параллелепипеда  Проецирование предметов на две и три взаимно перпендикулярные плоскости проекций - презентация по Геометрии
Проецирование предметов на две и три взаимно перпендикулярные плоскости проекций - презентация по Геометрии Второй признак подобия треугольников
Второй признак подобия треугольников 11. 09. 13 Многоугольник. Выпуклый многоугольник. Четырехугольник.
11. 09. 13 Многоугольник. Выпуклый многоугольник. Четырехугольник.  ЭЛЕМЕНТЫ ТРИГОНОМЕТРИИ РАДИАННАЯ МЕРА УГЛА МОУ Василёвская СОШ Починковского р-на Нижегородской обл. Учитель: Архипкина И.В.
ЭЛЕМЕНТЫ ТРИГОНОМЕТРИИ РАДИАННАЯ МЕРА УГЛА МОУ Василёвская СОШ Починковского р-на Нижегородской обл. Учитель: Архипкина И.В. .Действия с векторами
.Действия с векторами  Применение подобия к доказательству теорем и решению задач
Применение подобия к доказательству теорем и решению задач Признаки равенства треугольников - презентация по Геометрии
Признаки равенства треугольников - презентация по Геометрии Такая известная теорема Пифагора - презентация по Геометрии_
Такая известная теорема Пифагора - презентация по Геометрии_ Занимательная математика Алгебра и начала математического анализа, 10 класс.
Занимательная математика Алгебра и начала математического анализа, 10 класс.  Длина окружности и площадь круга. Решение задач.
Длина окружности и площадь круга. Решение задач.  Проект «Математика в профессии «Повар, кондитер» Автор: преподаватель ГОУ СПО ПК № 33 Симоненко Е.Е.
Проект «Математика в профессии «Повар, кондитер» Автор: преподаватель ГОУ СПО ПК № 33 Симоненко Е.Е. Тема проекта Построение общих касательных к двум окружностям на плоскости.
Тема проекта Построение общих касательных к двум окружностям на плоскости.  Урок 2 9 класс
Урок 2 9 класс Выполнила Иванова Галина Ивановна преподаватель математики Кадетского Корпуса Лицея № 38
Выполнила Иванова Галина Ивановна преподаватель математики Кадетского Корпуса Лицея № 38 Справочное пособие по геометрии – 7 класс Школьникам Учителям Родителям
Справочное пособие по геометрии – 7 класс Школьникам Учителям Родителям