Симметрия кристаллов, текстур и элементы кристаллофизики

братом Полем Жаком), открыл также магнитный фазовый переход железа (точку Кюри), закон Кюри для парамагнетиков, но Нобелевская премия 1903 г. – за радиоактивность (совместно с женой Марией и А. Беккерелем).

Если на кристалл оказывается воздействие, то сохраняются лишь те элемен-ты симметрии, которые являются общими для кристалла и воздействия, – с учётом их взаимной ориентации. Механическое давление центросимметрично по 3-му закону Ньютона. Если у кристалла тоже есть центр инверсии, то под давлением он сохраняется – нет пьезоэлектричества. Но если у кристалла нет центра инверсии, то при некоторых вариантах деформации есть пьезоэффект.
Тетраэдр – тело ацентричное, но неполярное. Даже если красный шарик заряжен положительно, а синие – отрицательно, то центр тяжести отрицательных зарядов совпадает с красным шариком. Векторная сумма моментов связей равна нулю. Это обеспечивается наличием хотя бы одной оси -4 (а их тут три).
Тетраэдр -43m Одноосное сжатие (растяжение) ∞/mmm
вдоль оси -4 вдоль оси 3

Нет полярности, даже -4m2 3m
если связи полярны Нет поляризации Есть поляризация

картина кристалла всегда центросимметрична, даже если у самого кристалла нет центра инверсии. Иначе говоря, интенсивно-сти отражений от семейства плоскостей (hkl) в обе стороны одинаковы: I(hkl) = I(-h-k-l). Поэтому по дифракционной картине невозможно различить точечные группы, отличающиеся только центром симметрии, и симметрия дифракционных картин описыва-ется вместо 32 точечных групп всего одиннадцатью Лауэ-классами (первый столбец на предыдущем слайде). Например, если к классам 2 и m рентгенограмма добавляет центр инверсии, они оба, согласно теоремам 2 и 3, превращаются в 2/m.
Известны следующие решения этой проблемы.
1) Отсутствие центра инверсии однозначно доказывается наличием пьезоэлектрического эффекта. Но с микрокристаллом, керамикой, проводящим кристаллом проверка этого обычно невозможна.
2) Отсутствие центра инверсии однозначно доказывается генераци-ей второй оптической гармоники (ГВГ), например, превращением ИК излучения лазера 1,06 мкм в зелёное 0,53 мкм. Это можно делать и с порошками, если кристаллы достаточно прозрачны, хотя для практических применений эффекта ГВГ нужны монокристаллы.

же трудности с микрокристаллами, керамикой и проводниками, но принципиально важно другое: наличие пироэффекта однозначно доказывает отсутствие центра инверсии, но отсутствие пироэф-фекта ещё не означает наличия центра инверсии. Класс пироэлектриков - это подкласс класса пьезоэлектриков: есть 11 ацентричных, но неполярных классов (см. среднюю колонку в таблице выше).
4) Иногда отсутствие центра инверсии ярко выражено в форме кристаллов.

Кроме того, ацентричная форма могла получиться из-за условий роста по принципу Кюри. Если, например, кристалл растёт на дне стакана, то доступ вещества снизу затруднён, и там получается вмятина
– пирамида роста. Даже если структура имеет центр
инверсии или горизонтальную плоскость симметрии
или ось 2, то форма кристалла её теряет. А если внеш-
няя форма кристалла центросимметрична (например,
параллелепипед), это ещё не значит, что центр инверсии
действительно есть. Сегнетоэлектрики обычно растут
выше точки Кюри, а СЭ фазовый переход на форму не влияет.

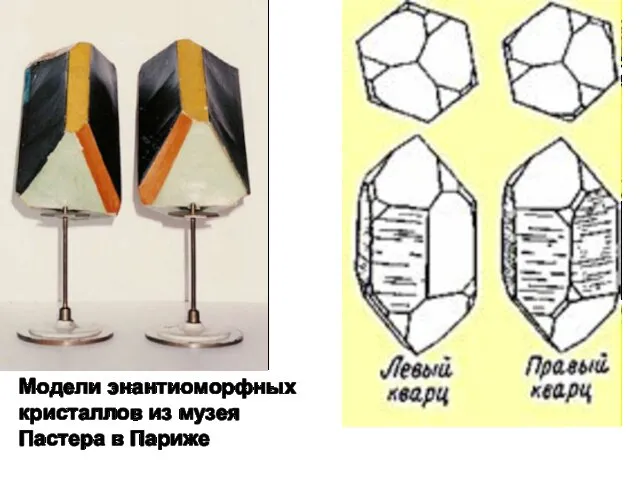
Так Луи Пастер (1822-1895) в 1848 г. разделил пинцетом энантиомеры тартрата натрия-аммония. Но хорошо огранённые кристаллы получаются не всегда.

инверсии и плоскости симметрии - хиральность. Но не все кристаллы достаточно прозрачны. К тому же, ахиральность не означает центросимметричности. Например, группа -43m не хиральна, но и не центросимметрична.
6) Аномальное рассеяние рентгеновских лучей. Закон Фриделя основан на том, что рентгеновские лучи рассеиваются атомами без изменения фазы. Но вблизи края поглощения происходит аномальное рассеяние с изменением фазы, и закон Фриделя нарушается: интенсивности отражений hkl и –h –k –l становятся неравными, если в кристалле нет центра инверсии. Их различие невелико, но современная аппаратура позволяет его обнаружить. Хуже другое: далеко не для каждого вещества (особенно если там нет тяжёлых атомов) можно подобрать трубку с излучением, близким к краю поглощения. В этом смысле очень ценно синхротронное излучение, из которого можно выбрать любую желаемую длину волны.
Даже если отсутствие центра инверсии уже установлено другими методами, аномальное рассеяние сохраняет решающее значение для определения абсолютных конфигураций оптически активных веществ, то есть позволяет рентгеновским методом различать "правые" и "левые" конфигурации атомных структур, что особенно важно для биохимии и молекулярной биологии. На некоторых монокристальных дифрактометрах есть сразу две рентгеновские трубки: жесткое излучение (MoKα) – для обычного структур-ного анализа, а более мягкое (CuKα, FeKα) – для аномального рассеяния.

Проблема обнаружения центра инверсии

чисто дифракционным методом и без аномального рассеяния, в том числе даже порошковым методом, без монокристаллов. Это основано на том, что винтовые оси, в отличие от поворотных, и плоскости скользящего отражения, в отличие от зеркальных, проявляют себя в систематических погасаниях определённых типов отражений. Если они обнаружены, это доказывает наличие определённых элементов симметрии и в некоторых случаях позволяет сделать однозначный вывод. Например, если у ромбического кристалла обнаружены погасания, соответствующие трём взаимно перпендикулярным плоскостям скользящего отражения, значит, центр инверсии есть, точечная группа mmm. И наоборот, если у ромбического кристалла обнаружены погасания, соответствующие трём взаимно перпендикулярным винтовым осям 21, а других погасаний нет, значит, нет и центра инверсии, точечная группа 222. Но если у кристалла таких погасаний нет, то вопрос о наличии или отсутствии центра инверсии остаётся нерешённым: зеркальные плоскости и поворотные оси не выявляются по погасаниям.

Проблема обнаружения центра инверсии

проблему в отсутствие данных, перечисленных выше, на этапе уточнения структуры. Если модель структуры без центра инверсии обеспечивает лучшее согласие между вычисленными и наблюдаемыми интенсивностями, чем центросимметричная модель, то делается вывод, что верна первая. Это часто ведёт к ошибкам. Низкосимметричная модель имеет больше переменных параметров и уже по одному этому может обеспечить лучшую подгонку интенсив-ностей, даже если реальная симметрия выше. В литературе есть множество случаев, когда структура описывалась как ацентричная, хотя тот же набор дифракционных данных, без дополнительных экспериментов, можно было убедительнее описать в рамках центросимметричной структуры. Например, 279 из 1280 расшифровок c ацентричной пространственной группой P1, опубликованных к 1998 г. в Cambridge Structural Database, т.е. 22%, имели заниженную сим-метрию. В большинстве этих случаев структура хорошо соответству-ет центросимметричной группе P-1, а в ряде случаев даже сингония оказывается выше: моноклинная, а не триклинная [R.E. Marsh, Acta Cryst. B55 (1999) 931]. Доступность аппаратуры и программ привела к тому, что расшифровки стали делать люди без должной квалифика-ции, и лишь недавно (после 2003 г.) ситуация начала улучшаться, т.к. стали применяться специальные программы поиска таких ошибок.

Проблема обнаружения центра инверсии

для описания свойств только в случае изотропных сред и объектов (жидкостей, стёкол, иногда – кубических кристаллов), а в общем случае одной цифры недо-статочно. Тензор характеризуется матрицей параметров, описывающих зависимость явления от ориентации. Матрицы и тензоры могут быть разных рангов. Различают:
полевые тензоры – описывающие физические поля, воздействую-щие на кристалл или возникающие в кристалле в результате воздействия;
материальные тензоры, описывающие свойство материала, т.е. связь между воздействием и результатом.
Ранг материального тензора равен сумме рангов воздействия и результата. Пример. Если к кристаллу приложено электрическое поле, то в нём возникает ток. Это явление описывается удельной электропроводностью σ (См/м = А/(В м) по закону Ома:
j = σ E, где j – плотность тока (А/м2), E – напряжённость поля (В/м).
Но в анизотропной среде векторы j и E (тензоры 1 ранга) не обязательно параллельны! Направление тока не всегда точно совпадает с направлением поля! Поэтому σij – тензор 2-го ранга:
ji = σij Ej

проницаемость, коэффициент диффузии…)
Пусть вектор воздействия а определяется координатами а1, а2, а3, а вектор – результат с – координатами с1, с2, с3. Связь между ними задаётся системой уравнений: c1 = U11 a1 + U12 a2 + U13 a3
c2 = U21 a1 + U22 a2 + U23 a3
c3 = U31 a1 + U32 a2 + U33 a3
матрица коэффициентов которой описывает материальный тензор Uik:

В сокращённой записи ci = Uik ak
У такого тензора в общем случае 9 компонент, но перечисленные выше тензоры симметричны, т.е. Uik = Uki, и тогда число независимых компонент понижается до 6 в случае триклинной сингонии, и до меньшего числа при более высокой симметрии (см. следующий слайд).
Сокращённые обозначения индексов:
11→1, 22→2, 33→3, 23=32→4, 31=13→5, 12=21→6
Uik = | U1 U2 U3 U4 U5 U6 |

Измерив независимые компоненты, можно вычислить свойства
для любой ориентации

U3 U4 U5 U6
Моноклинная: U1 U2 U3 0 U5 0 (если особая ось Y)
Ромбическая: U1 U2 U3 0 0 0
Средние: U1 U1 U3 0 0 0
Кубическая: U1 U1 U1 0 0 0
Заметьте, что число независимых компонент тензора второго ранга равно числу независимых параметров элементарной ячейки.

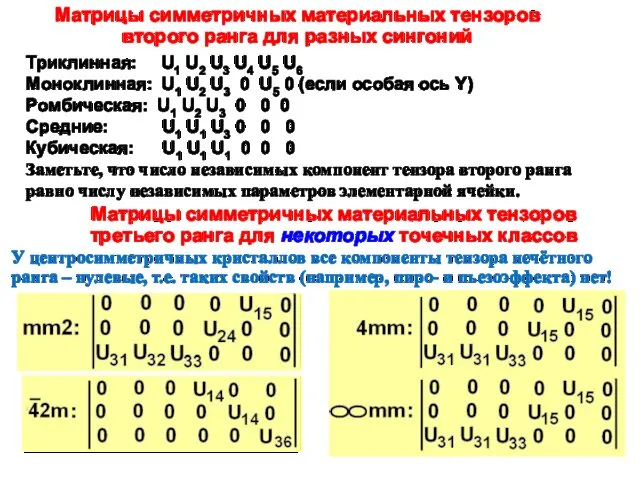
Матрицы симметричных материальных тензоров
третьего ранга для некоторых точечных классов

У центросимметричных кристаллов все компоненты тензора нечётного
ранга – нулевые, т.е. таких свойств (например, пиро- и пьезоэффекта) нет!