Содержание
- 2. Содержание Текущий контроль Основные допущения Способы задания бинарных отношений Алгоритмы ранжирования объектов Классификация бинарных отношений Метод
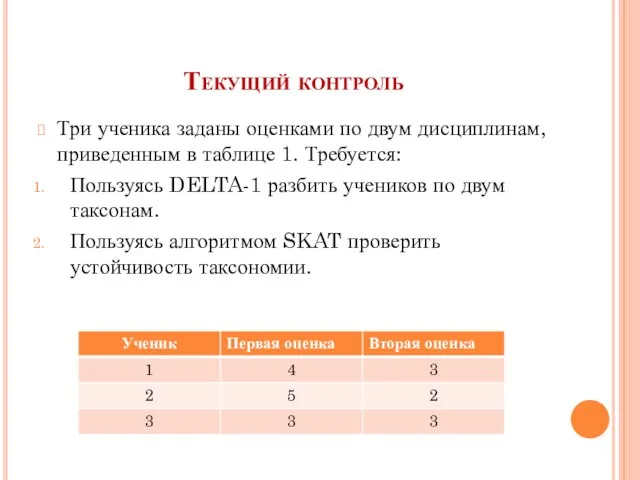
- 3. Текущий контроль Три ученика заданы оценками по двум дисциплинам, приведенным в таблице 1. Требуется: Пользуясь DELTA-1
- 4. Допущения 1) Отсутствие количественных характеристик предпочтительности одной альтернативы по сравнению с другой; 2) Для каждой пары
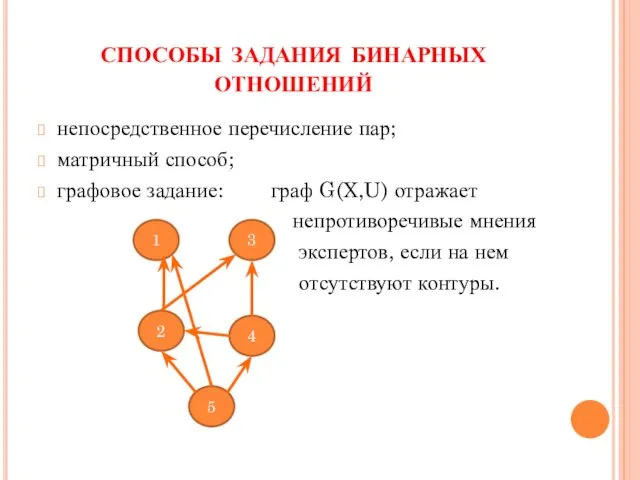
- 5. способы задания бинарных отношений непосредственное перечисление пар; матричный способ; графовое задание: граф G(X,U) отражает непротиворечивые мнения
- 6. Алгоритм ранжирования объектов в порядке ухудшения Шаг 1. i = 1. Шаг 2. На множестве вершин
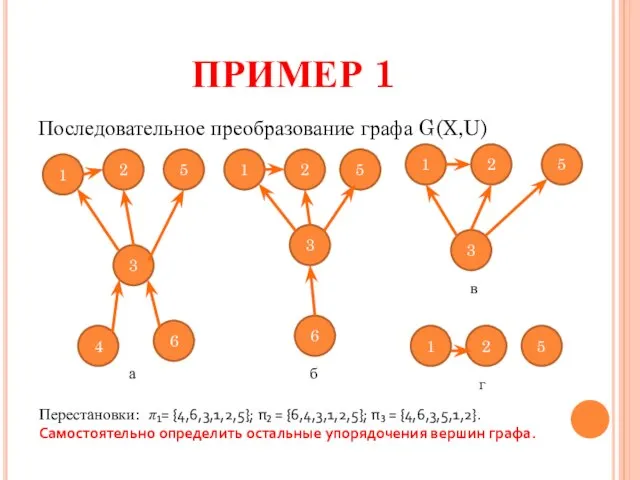
- 7. ПРИМЕР 1 Последовательное преобразование графа G(X,U) 1 5 3 2 2 6 5 1 4 3
- 8. САМОСТОЯТЕЛЬНО Дать пошаговое описание упорядочения вершин графа G(X,U), не содержащего контуров, в порядке «улучшения» вершин. Упорядочить
- 9. Программная реализация прямого и обратного упорядочений вершин
- 10. Классификация бинарных отношений В теории выбора используются три типа отношений: эквивалентности, порядка; доминирования.
- 11. Используемые термины Бинарное отношение R на множестве X нарывается: рефлексивным, если антирефлексивным, если симметричным, если асимметричным,
- 12. Используемые термины сильнотранзитивным, если отношение R одновременно транзитивно и отрицательно транзитивно. Отношение эквивалентности (~) рефлексивно, симметрично
- 13. пример практического использования бинарных отношений Группы экспертов оценивают пары поданных на конкурс проектов, пользуясь отношениями эквивалентности
- 14. Избавление от противоречивых оценок Одним из подходов, позволяющим избавиться от противоречий, является отказ от мнений нескольких
- 15. Формальная постановка задачи где: A(G) - множество контуров на ориентированном графе G(X, U); U(a) – подмножество
- 16. Метод Делфи Четыре основных этапа метода Делфи: Раздача анкет, сбор оценок, их обобщение и определение разброса
- 17. Противоречивые мнения экспертов Наличие контуров на графе G(X,U) приводит к выводу о наличии противоречий во мнениях
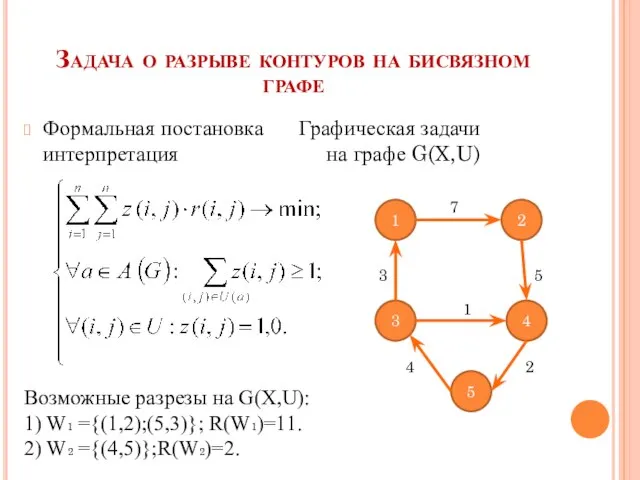
- 18. Задача о разрыве контуров на бисвязном графе Формальная постановка Графическая задачи интерпретация на графе G(X,U) 1
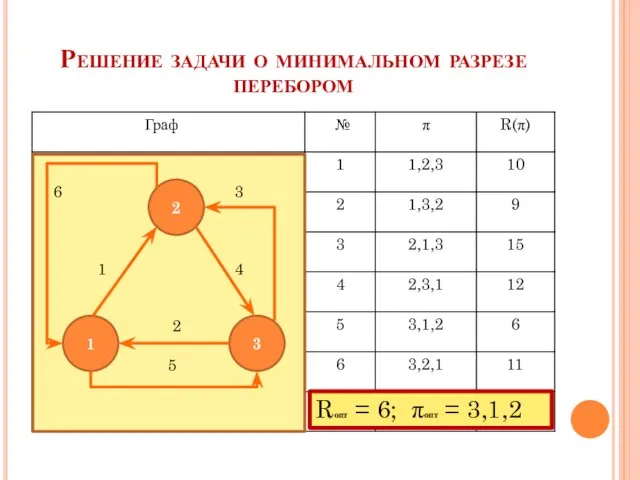
- 19. Решение задачи о минимальном разрезе перебором 2 3 1 6 3 1 4 2 5 Rопт
- 20. Программа поиска минимального разреза на бисвязном взвешенном графе
- 22. Скачать презентацию












 Презентация по информатике Алгоритм и его формальное исполнение
Презентация по информатике Алгоритм и его формальное исполнение  Презентация "Основы логики 4 класс" - скачать презентации по Информатике
Презентация "Основы логики 4 класс" - скачать презентации по Информатике Мобильные сервисы в сетях 4G
Мобильные сервисы в сетях 4G ЛЕКЦІЯ 1 Обробка інформації
ЛЕКЦІЯ 1 Обробка інформації Общие сведения о языке программирования python
Общие сведения о языке программирования python Искусственный интеллект в сетях связи. Вводная лекция
Искусственный интеллект в сетях связи. Вводная лекция Операторы управления ходом выполнения программы в С++
Операторы управления ходом выполнения программы в С++ Крылов А.П. Лабораторная работа №2 Коммуникативная природа информационного общества
Крылов А.П. Лабораторная работа №2 Коммуникативная природа информационного общества Обеспечение безопасности беспроводной локальной сети
Обеспечение безопасности беспроводной локальной сети Топологии компьютерных сетей
Топологии компьютерных сетей Строковый тип данных
Строковый тип данных Особенности нового регулирования сферы применения контрольно-кассовой техники
Особенности нового регулирования сферы применения контрольно-кассовой техники Стратегический анализ
Стратегический анализ Программирование на Python
Программирование на Python Анализ программно-аппаратных средств
Анализ программно-аппаратных средств Системы управления базами данных (лекция 01)
Системы управления базами данных (лекция 01) Аттестационная работа. Методическая разработка по выполнению проекта JPEG - формат графического файла
Аттестационная работа. Методическая разработка по выполнению проекта JPEG - формат графического файла История сети Интернет
История сети Интернет Логические основы ЭВМ
Логические основы ЭВМ Книги для выявления и развития одаренности у детей
Книги для выявления и развития одаренности у детей Средства массовой информации (СМИ)
Средства массовой информации (СМИ) Программирование на языке Python
Программирование на языке Python Что такое система. Информационные системы и базы данных
Что такое система. Информационные системы и базы данных Информационная система учета и планирования работы салона красоты
Информационная система учета и планирования работы салона красоты Типичные нарушения законодательства о защите прав потребителей и рекламе при осуществлении интернет-торговли
Типичные нарушения законодательства о защите прав потребителей и рекламе при осуществлении интернет-торговли Программы воспроизведения звуковых файлов Windows Media Player
Программы воспроизведения звуковых файлов Windows Media Player Делегаты (C#, Лекция 5)
Делегаты (C#, Лекция 5) Реляциялық МҚ жобалау жане жобалау кезеңдері
Реляциялық МҚ жобалау жане жобалау кезеңдері