Содержание
- 2. Содержание Простейшие тригонометрические уравнения Простейшие тригонометрические неравенства
- 3. Простейшие тригонометрические уравнения Определение арксинуса. Уравнение sin t = aa. Определение арккосинуса. Уравнение cos t =
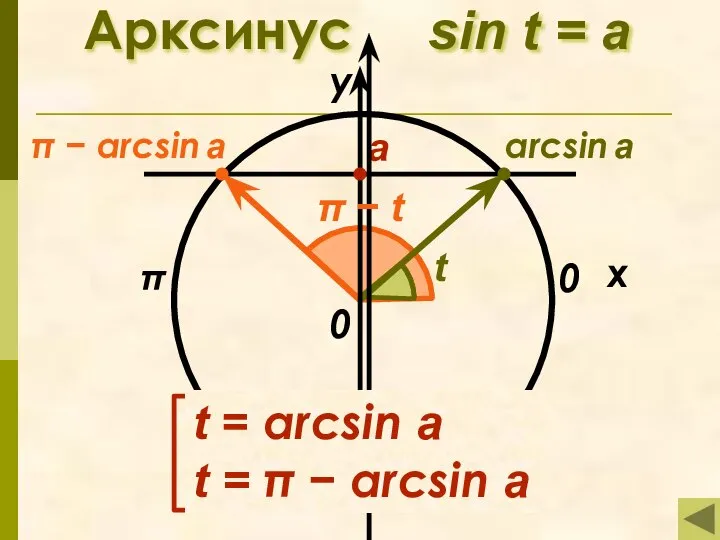
- 4. Определение арксинуса Арксинусом числа а называется такой угол из промежутка [− 0,5π; 0,5π], синус которого равен
- 5. Арксинус sin t = а π x у 0 а arcsin a π − arcsin a
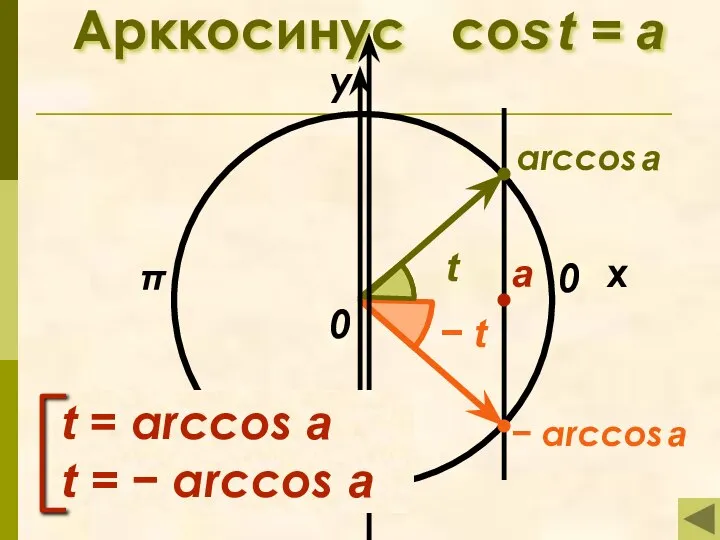
- 6. Определение арккосинуса Арккосинусом числа а называется такой угол из промежутка [ 0; π], косинус которого равен
- 7. Арккосинус cos t = а π x у 0 а arccos a − arccos a 0
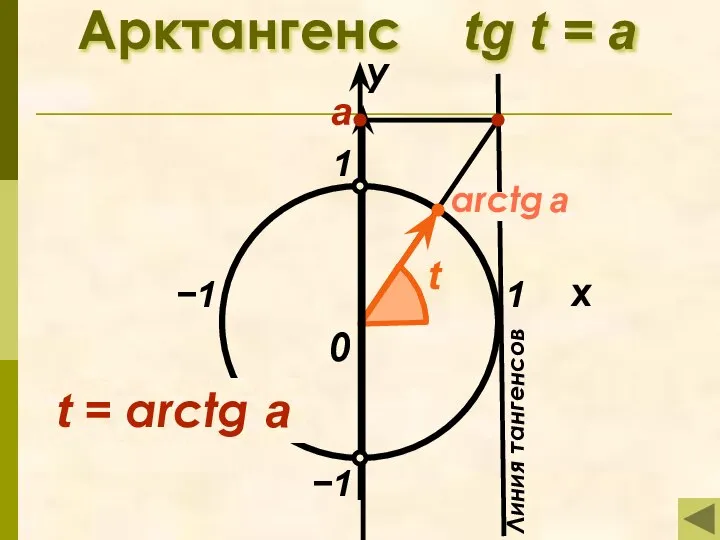
- 8. Определение арктангенса Арктангенсом числа а называется такой угол из промежутка (− 0,5π; 0,5π), тангенс которого равен
- 9. arctg a Арктангенс tg t = а 1 x у 0 t t = arctg a
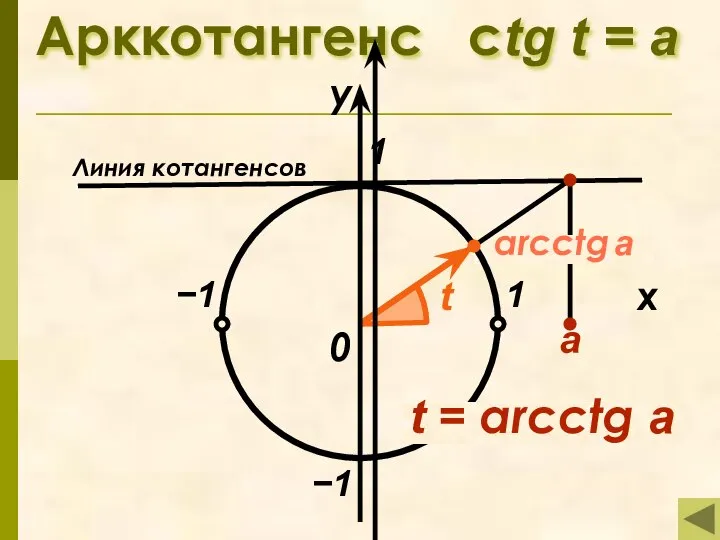
- 10. Определение арккотангенса Арккотангенсом числа а называется такой угол из промежутка (0; π), котангенс которого равен а.
- 11. arcctg a Арккотангенс сtg t = а 1 x у 0 t t = arcсtg a
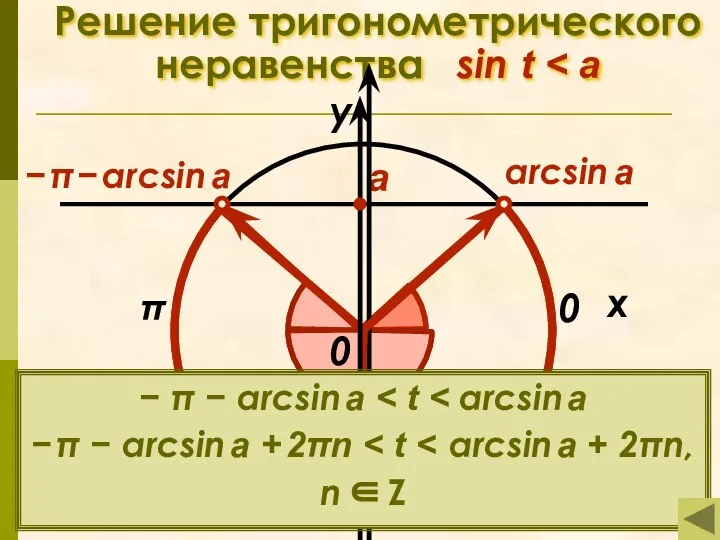
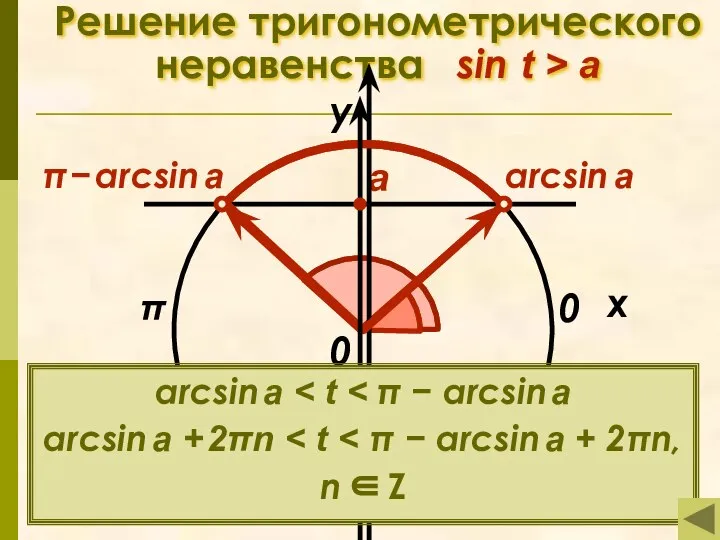
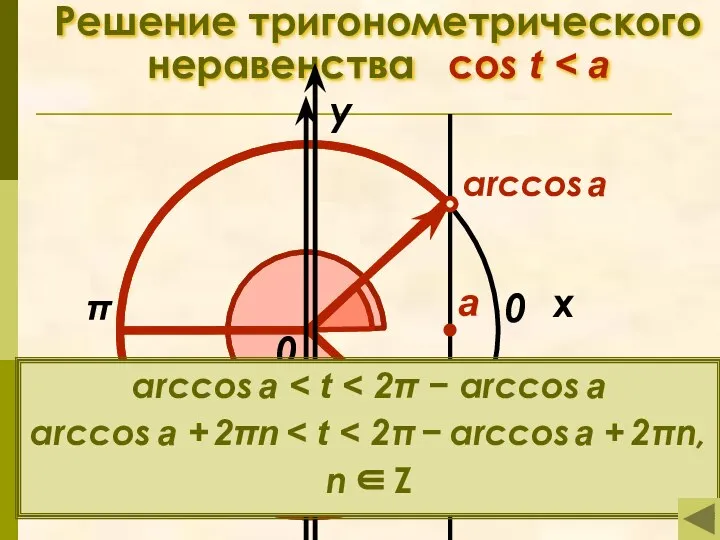
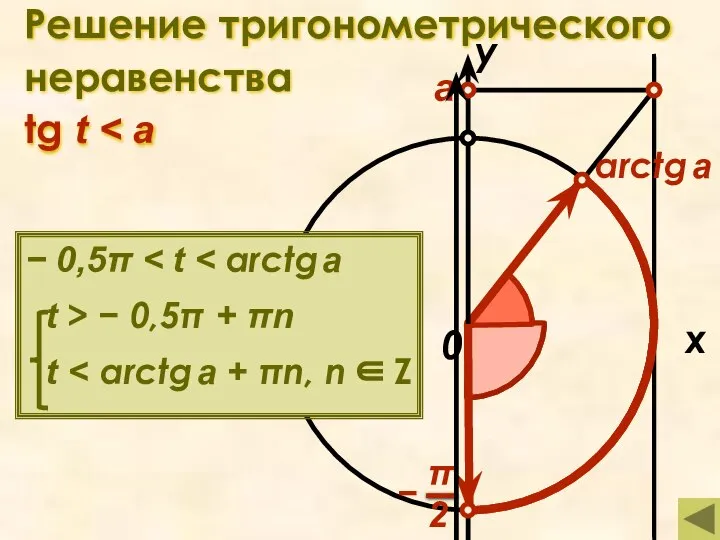
- 12. Простейшие тригонометрические неравенства Решение тригонометрического неравенства Решение тригонометрического неравенства sin t Решение тригонометрического неравенства Решение тригонометрического
- 13. Решение тригонометрического неравенства sin t π x у 0 а arcsin a − π − arcsin
- 14. Решение тригонометрического неравенства sin t > a π x у 0 а arcsin a π −
- 15. Решение тригонометрического неравенства cos t π x у 0 а arccos a 2π − arccos a
- 16. Решение тригонометрического неравенства cos t > a π x у 0 а arccos a − arccos
- 17. Решение тригонометрического неравенства tg t x у 0 а arctg a − 0,5π t > −
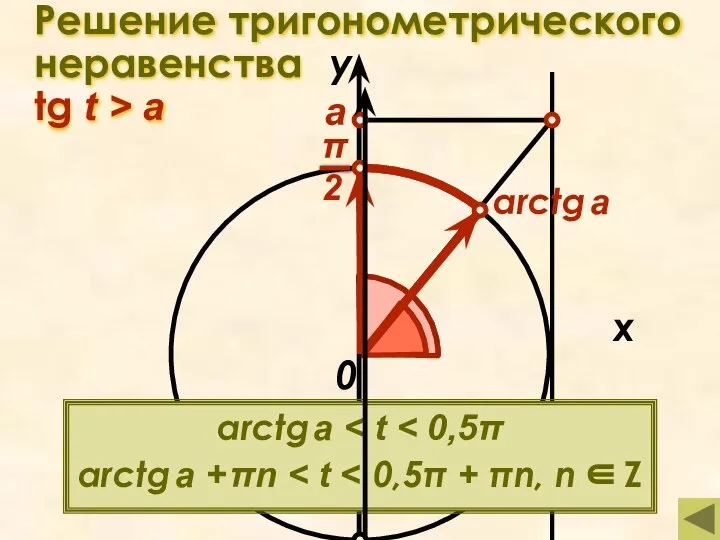
- 18. Решение тригонометрического неравенства tg t > a x у 0 а arctg a arctg a arctg
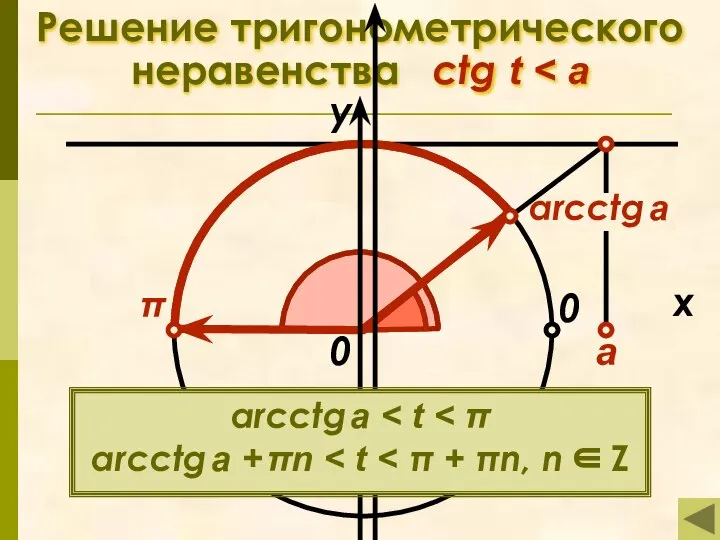
- 19. arcctg a Решение тригонометрического неравенства ctg t π x у 0 а 0 arcctg a arcctg
- 21. Скачать презентацию








 Теорема Пифагора
Теорема Пифагора Основы теории ошибок измерений. Виды измерений и погрешностей
Основы теории ошибок измерений. Виды измерений и погрешностей Решение задач с помощью квадратных уравнений (по материалам Бородинского сражения)
Решение задач с помощью квадратных уравнений (по материалам Бородинского сражения) Здравствуй, школа! Первые уроки математики в 6 классе.
Здравствуй, школа! Первые уроки математики в 6 классе. Геометрические тела. Объёмы и поверхности.
Геометрические тела. Объёмы и поверхности. Конкурс «Математика в жизни семьи» Илларионова Татьяна Юрьевна Учитель математики МОУ Жердевской СОШ №1
Конкурс «Математика в жизни семьи» Илларионова Татьяна Юрьевна Учитель математики МОУ Жердевской СОШ №1  Односторонние пределы
Односторонние пределы Вычисление площадей плоских фигур. Геометрические приложения. Пример 1
Вычисление площадей плоских фигур. Геометрические приложения. Пример 1 Уравнения и неравенства с двумя переменными
Уравнения и неравенства с двумя переменными Проект по математике. Теория вероятности
Проект по математике. Теория вероятности Графический диктант (зрительный)
Графический диктант (зрительный) Преобразование выражений, содержащих квадратные корни Учитель математики МБОУ гимназии № 82 г. Краснодара Чернова Татьяна Викто
Преобразование выражений, содержащих квадратные корни Учитель математики МБОУ гимназии № 82 г. Краснодара Чернова Татьяна Викто Степень с рациональным показателем. Определения и свойства степени с рациональным показателем
Степень с рациональным показателем. Определения и свойства степени с рациональным показателем Аксиомы стереометрии
Аксиомы стереометрии Поворот
Поворот Презентация на тему свойства степени n-ой степени
Презентация на тему свойства степени n-ой степени  Планирование эксперимента для применения корреляционного анализа
Планирование эксперимента для применения корреляционного анализа Две теоремы о функциональной полноте. ДМ.10
Две теоремы о функциональной полноте. ДМ.10 Презентация по математике "ВЕСЕЛАЯ МАТЕМАТИКА" - скачать
Презентация по математике "ВЕСЕЛАЯ МАТЕМАТИКА" - скачать  Неопределенный интеграл. Интегрирование функций, содержащих квадратный трехчлен. Лекция 3
Неопределенный интеграл. Интегрирование функций, содержащих квадратный трехчлен. Лекция 3 Геометрические основы компьютерной графики
Геометрические основы компьютерной графики Деление дробей. Задачи для 6 класса
Деление дробей. Задачи для 6 класса Лайфхаки для решения задач по математике
Лайфхаки для решения задач по математике Урок-путешествие в страну положительных и отрицательных чисел
Урок-путешествие в страну положительных и отрицательных чисел Конспект урока математики. 4класс.
Конспект урока математики. 4класс.  Тренажёр Помоги Снеговику. Математика 1 класс
Тренажёр Помоги Снеговику. Математика 1 класс Методика обучения решению составных задач
Методика обучения решению составных задач Показательная функция, ее свойства и график. Конспект урока c использованием информационно-коммуникационных технологий
Показательная функция, ее свойства и график. Конспект урока c использованием информационно-коммуникационных технологий