Содержание
- 2. Плоскость и её основные уравнения Рассмотрим плоскость P в прямоугольной декартовой системе координат.
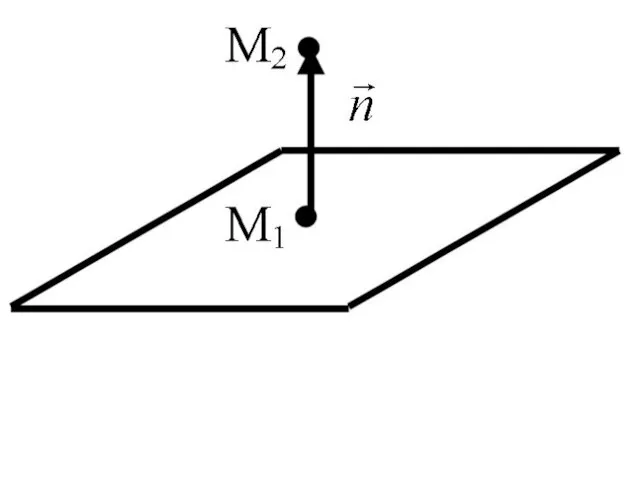
- 3. Положение плоскости вполне определяется точкой и вектором нормали
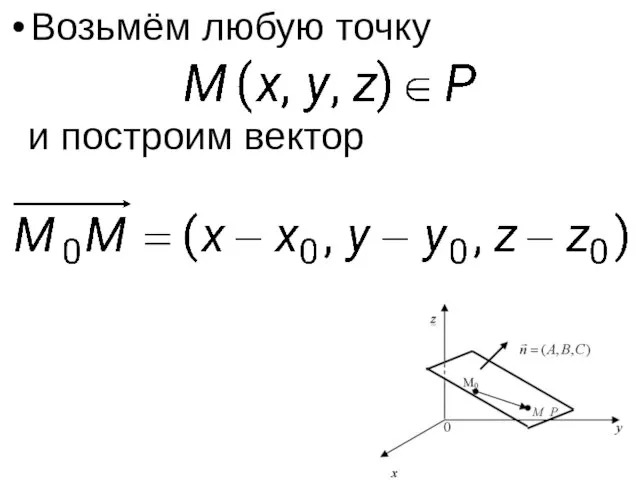
- 5. Возьмём любую точку и построим вектор
- 6. Так как , то скалярное произведение или
- 7. Получили уравнение плоскости, заданной точкой и вектором нормали
- 8. Если в уравнении раскрыть скобки и обозначить то получим общее уравнение плоскости:
- 9. Теорема. Всякое уравнение вида определяет некоторую плоскость в пространстве.
- 10. Если в этом уравнении какой-либо из коэффициентов A, B, C равен нулю, то плоскость расположена параллельно
- 11. Например, при A = 0 плоскость By + Cz + D = 0 параллельна оси Ox;
- 12. Пусть в уравнении ни один из коэффициентов не равен 0. Перепишем это уравнение в виде разделим
- 13. Получим уравнение плоскости в отрезках:
- 14. где a, b, c – это величины направленных отрезков, отсекаемых плоскостью на осях координат
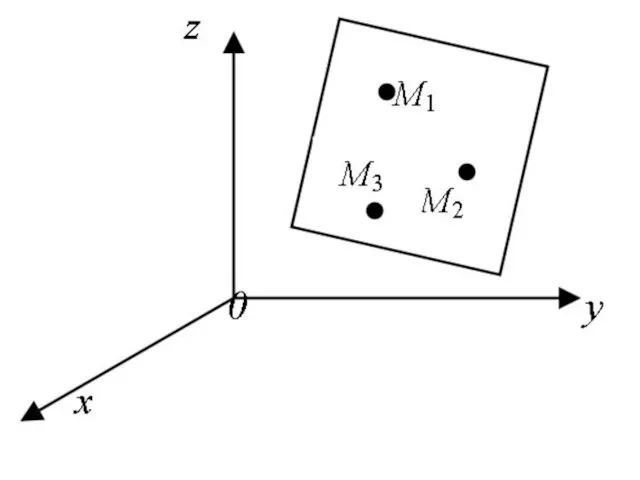
- 16. Если три точки не лежат на одной прямой, то через эти точки проходит единственная плоскость:
- 18. Уравнение плоскости, проходящей через три точки, имеет вид:
- 19. Пусть даны две плоскости и Угол φ между двумя плоскостями равен углу между их векторами нормали:
- 21. Расстояние d от точки до плоскости определяется по формуле
- 22. Пример. Даны две точки Записать уравнение плоскости, проходящей через точку M1 перпендикулярно вектору
- 23. Решение. Поскольку искомая плоскость перпендикулярна вектору , то в качестве вектора нормали возьмем вектор
- 25. Подставив теперь в уравнение а также координаты точки M1: получим уравнение
- 26. или – это и есть искомое общее уравнение плоскости
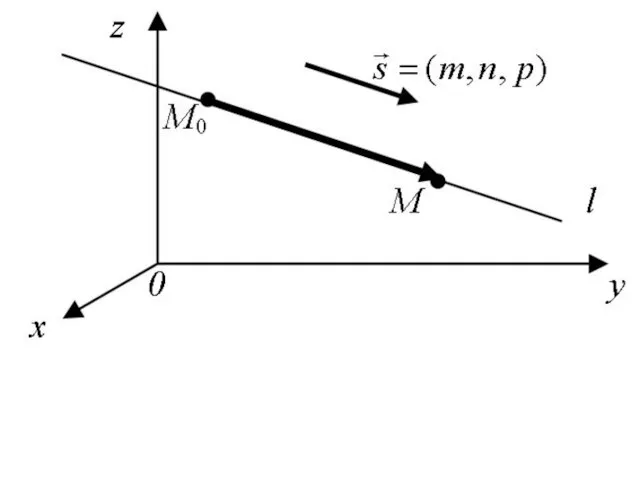
- 27. Прямая в пространстве и её основные уравнения Рассмотрим прямую l в прямоугольной декартовой системе координат. Положение
- 29. Возьмем любую точку и построим вектор , из условия коллинеарности этих векторов получим канонические уравнения прямой
- 30. Обозначим коэффициент пропорциональности через параметр t и выразим через t переменные x, y, z. Приходим к
- 31. Уравнение прямой, проходящей через две точки M1(x1, y1, z1) и M2(x2, y2, z2) , имеет вид:
- 32. Рассмотрим две плоскости P1 : A1x + B1y + C1z+ D1 = 0 и P2 :
- 33. Эта система называется общим уравнением прямой в пространстве.
- 34. Угол φ между двумя прямыми l1 и l2 равен углу между их направляющими векторами и
- 35. Угол ψ между прямой и плоскостью Ax + By + Cz + D = 0 определяется
- 36. Пример. Составить канонические и параметрические уравнения прямой, проходящей через точки M1(3; 2; -1) и M2(4; 2;
- 37. Решение. Подставляем в формулу координаты точек M1(3; 2; -1) и M2(4; 2; 1):
- 38. или – канонические уравнения прямой (нуль в знаменателе означает, что направляющий вектор перпендикулярен оси Oy, т.е.
- 39. Запишем параметрические уравнения прямой:
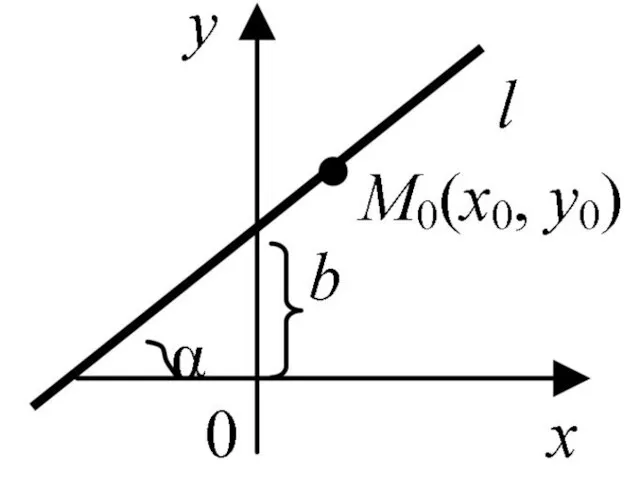
- 40. Прямая на плоскости и её основные уравнения Уравнение прямой с угловым коэффициентом k имеет вид или
- 41. где k = tg α – угловой коэффициент прямой, b – величина отрезка, отсекаемого этой прямой
- 43. Кроме того, прямую l на плоскости можно задать вектором нормали и точкой
- 45. Получим три уравнения, аналогичные уравнениям для плоскости: – уравнение прямой, заданной точкой и вектором нормали;
- 46. – общее уравнение прямой; – уравнение прямой в отрезках.
- 47. Прямая l на плоскости также определяется направляющим вектором и точкой
- 49. Получим еще 3 уравнения, аналогичные уравнениям прямой в пространстве: – каноническое уравнение прямой;
- 50. – параметрические уравнения прямой; – уравнение прямой, проходящей через две точки M1(x1, y1) и M2(x2, y2).
- 51. Угол между двумя прямыми, заданными уравнениями: l1: и l2: можно найти по формуле
- 52. при этом т.е. ,
- 53. Расстояние d от точки M1(x1, y1) до прямой Ax + By + C = 0 вычисляется
- 54. Пример. Записать уравнения прямых, проходящих через точку M(– 2, 1) параллельно и перпендикулярно прямой 3x –
- 55. Решение. Перепишем общее уравнение прямой 3x – 4y + 12 = 0, выразив из него переменную
- 56. Получили уравнение прямой с угловым коэффициентом k = 3/4. Запишем уравнение прямой и проходящей через точку
- 57. то или
- 58. Составим уравнение прямой , проходящей через точку M(– 2,1). Так как угловые коэффициенты перпендикулярных прямых связаны
- 59. или Прямые изображены на рис.
- 61. Скачать презентацию



























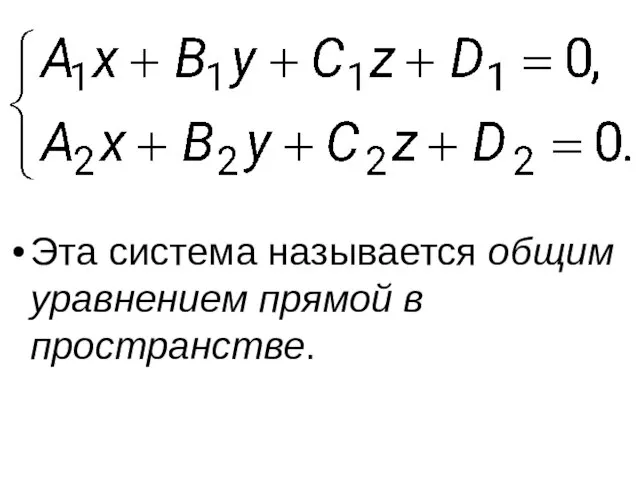











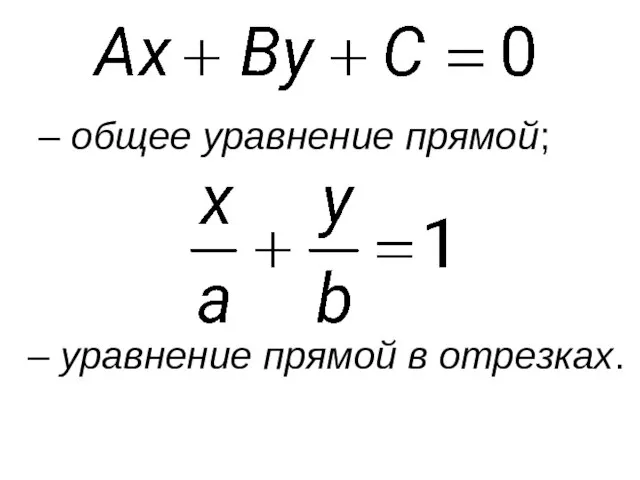

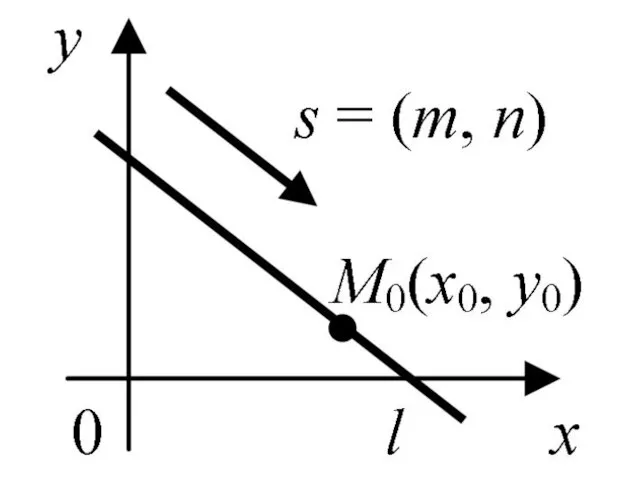

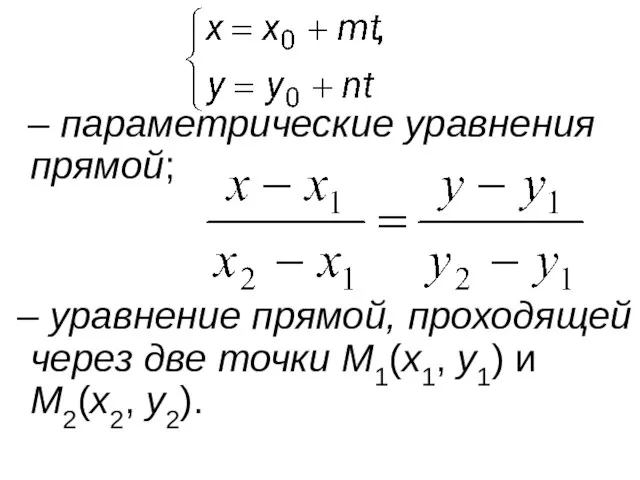

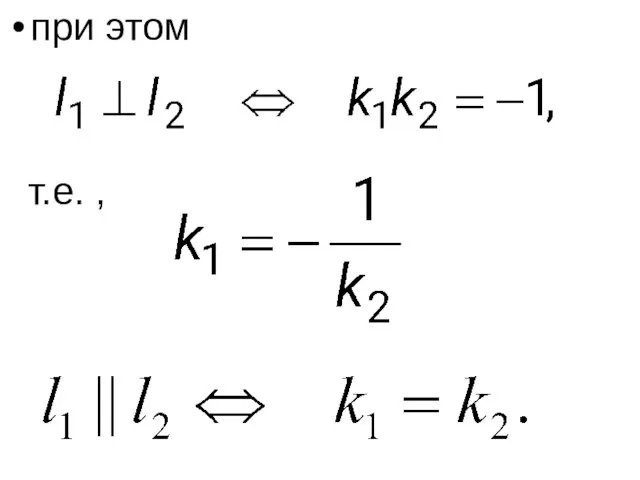




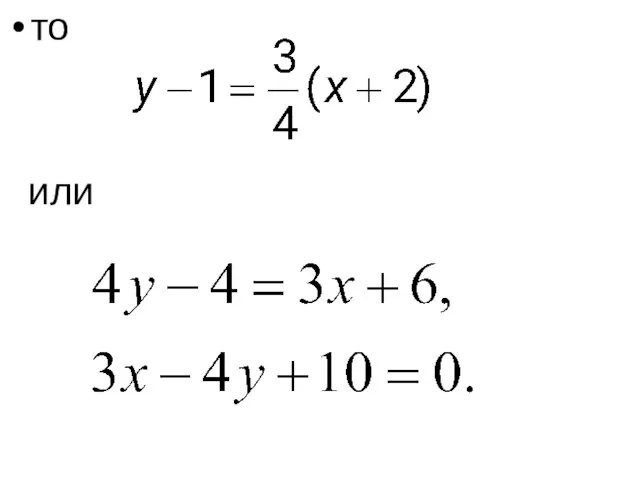

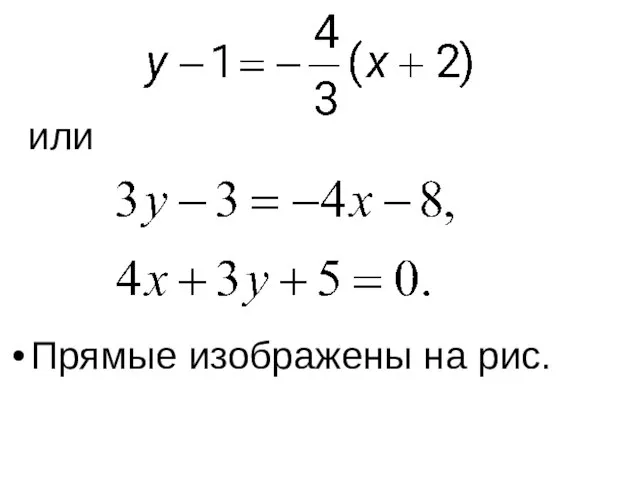
 Методы решения систем уравнений второй степени. 9 класс
Методы решения систем уравнений второй степени. 9 класс Первообразная. Правила нахождения первообразных
Первообразная. Правила нахождения первообразных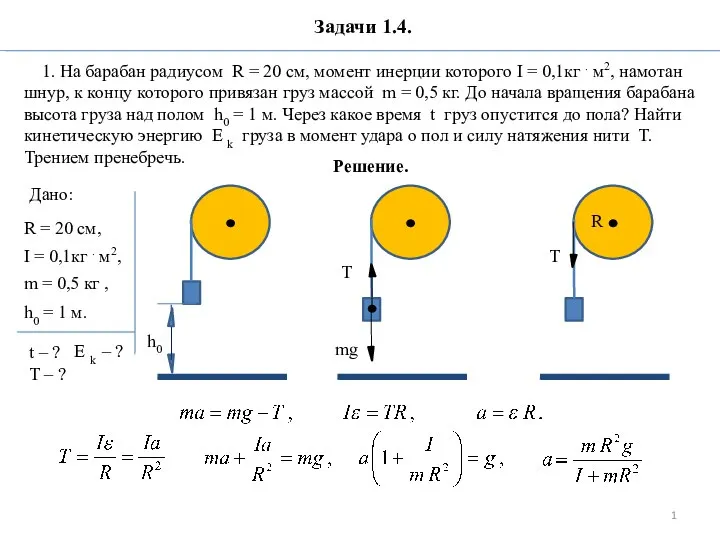 Задачи 1.4
Задачи 1.4 Вводный урок 1. 8 класс. Геометрия
Вводный урок 1. 8 класс. Геометрия Показательные функции, уравнения, неравенства
Показательные функции, уравнения, неравенства Комбинаторика и элементы теории вероятностей и статистики в задачах ГИА
Комбинаторика и элементы теории вероятностей и статистики в задачах ГИА Контрольная работа по математике. 6 класс
Контрольная работа по математике. 6 класс Оценка точности функций
Оценка точности функций Профессиональная задача на определение стоимости услуг за перевозку
Профессиональная задача на определение стоимости услуг за перевозку Треугольник. Тест. Задания в группах
Треугольник. Тест. Задания в группах Площадь фигур
Площадь фигур Обработка экспериментальных данных. Счетная обработка полученных данных. Расчет относительных величин
Обработка экспериментальных данных. Счетная обработка полученных данных. Расчет относительных величин Презентация по математике "Конкурс «А, ну-ка, девочки» по математике для учащихся 7 класса" - скачать
Презентация по математике "Конкурс «А, ну-ка, девочки» по математике для учащихся 7 класса" - скачать 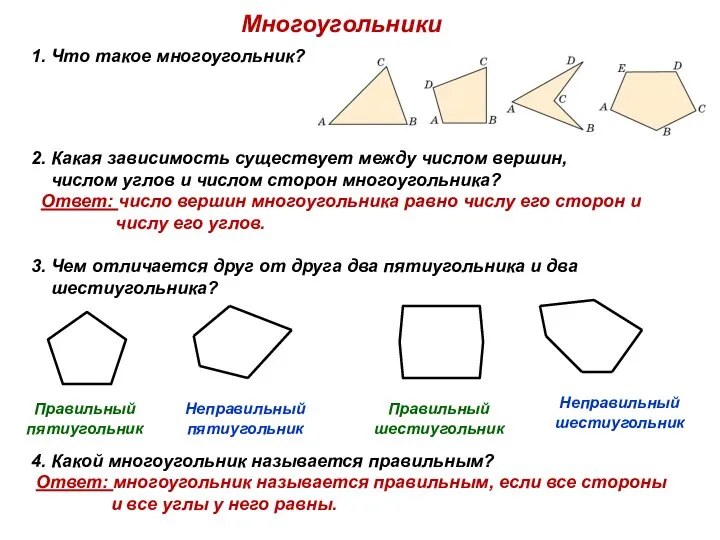 Многоугольники
Многоугольники Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Формула квадрата разности
Формула квадрата разности Урок математики 3 класс
Урок математики 3 класс  Погрешности результатов измерений
Погрешности результатов измерений Презентация по математике "Решение текстовых задач" - скачать бесплатно_
Презентация по математике "Решение текстовых задач" - скачать бесплатно_ Объём цилиндра в заданиях ЕГЭ
Объём цилиндра в заданиях ЕГЭ Домашнее задание
Домашнее задание Презентация на тему Деление чисел 5 класс
Презентация на тему Деление чисел 5 класс Алгебра. Прикладная математика и информатика
Алгебра. Прикладная математика и информатика Количество вещества
Количество вещества Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Примеры комбинаторных задач
Примеры комбинаторных задач Многогранники. Тела вращения. Тема 8
Многогранники. Тела вращения. Тема 8 Презентация по математике "Решение логарифмических уравнений и неравенств" - скачать
Презентация по математике "Решение логарифмических уравнений и неравенств" - скачать