Содержание
- 2. ЦЕЛЬ ЛЕКЦИИ Ознакомиться со способами отбора корней нелинейных уравнений
- 3. Какие уравнения называются нелинейными Нелинейными уравнениями называются уравнения вида , Данная функция является нелинейной
- 4. Нелинейные функции делятся на: – нелинейная алгебраическая функция вида – трансцендентные функции – тригонометрические, обратные тригонометрические,
- 5. Решением нелинейного уравнения является такая точка ,которая при подстановке в данное уравнение обращает его в тождество.
- 6. Нахождение таких решений и составляет основу численных методов и вычислительной математики Решение нелинейных уравнений распадается на
- 7. На первом этапе необходимо исследовать уравнение и выяснить, имеются корни или нет. Если корни имеются, то
- 8. Первый способ отделения корней – графический. Исходя из уравнения, можно построить график функции . Тогда точка
- 9. Если имеет сложный вид, то представим ее в виде разности двух функций Так как , то
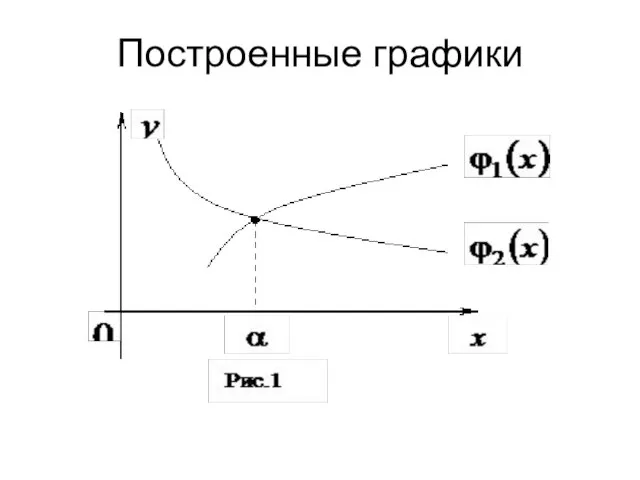
- 10. Построенные графики
- 11. ПРИМЕР 1 Пусть дано нелинейное уравнение вида . Решим его графическим методом. Для этого представим уравнение
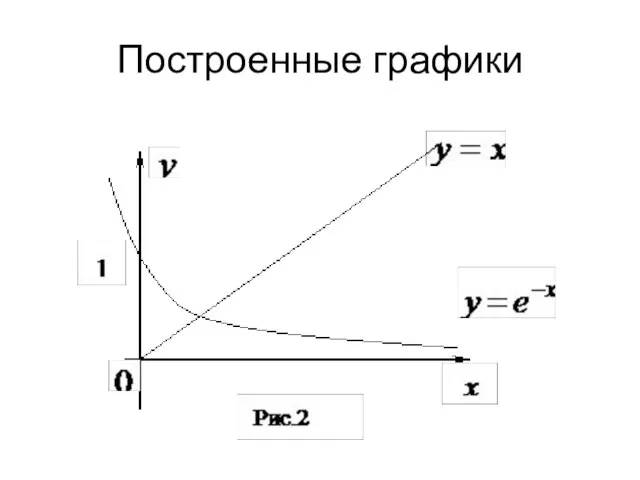
- 12. Построенные графики
- 13. ПРИМЕР 2 Пусть задано нелинейное уравнение вида или . Построив два графика функций и , видим,
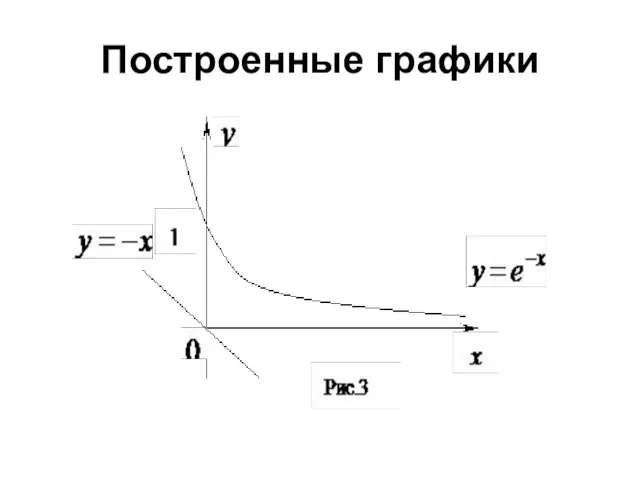
- 14. Построенные графики
- 15. ПРИМЕР 3 Дано нелинейное уравнения вида с помощью аналогичных преобразований и построений получим, что исходное уравнение
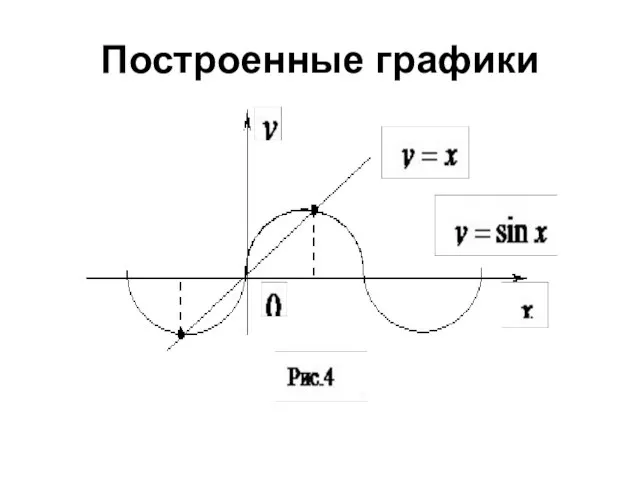
- 16. Построенные графики
- 17. Второй способ отделения корней нелинейных уравнений – АНАЛИТИЧЕСКИЙ В этом случае процесс отделения корней нелинейных уравнений
- 18. ТЕОРЕМА 1 Если функция непрерывна на отрезке и меняет на концах отрезка знак (т.е. ) то
- 19. ТЕОРЕМА 2 Если функция непрерывна на отрезке , выполняется условие вида и производная сохраняет знак на
- 20. ТЕОРЕМА 3 Если функция является многочленом степени и на концах отрезка меняет знак, то на имеется
- 21. При АНАЛИТИЧЕСКОМ методе исследований необходимо выявить интервалы монотонности функции . Для этого необходимо вычислить критические точки
- 22. Тогда вся числовая ось разбивается на интервалы монотонности . На каждом из них определяется знак производной
- 24. Скачать презентацию

















 МОУ СОШ №256 г.Фокино.
МОУ СОШ №256 г.Фокино.  Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Николай Иванович Лобачевский Конкурс презентаций «Великие люди России»
Николай Иванович Лобачевский Конкурс презентаций «Великие люди России»  Презентация на тему 2 класс Математический диктант № 5
Презентация на тему 2 класс Математический диктант № 5 Древний Вавилон
Древний Вавилон Аттестационная работа. Решение нестандартных задач по математике
Аттестационная работа. Решение нестандартных задач по математике Теория вероятностей
Теория вероятностей Тест по теме: "Скалярное произведение векторов". Вариант 2
Тест по теме: "Скалярное произведение векторов". Вариант 2 Прямоугольный параллелепипед
Прямоугольный параллелепипед Средняя линия треугольника
Средняя линия треугольника ОГЭ - 2016. Открытый банк заданий по математике. Модуль Геометрия
ОГЭ - 2016. Открытый банк заданий по математике. Модуль Геометрия Аттестационная работа. Решение логарифмических неравенств
Аттестационная работа. Решение логарифмических неравенств Прямоугольная система координат на плоскости 6 класс - презентация__________________________________________________________________________________________________________________
Прямоугольная система координат на плоскости 6 класс - презентация__________________________________________________________________________________________________________________ Сложение с переходом через десяток
Сложение с переходом через десяток Возрастание и убывание функций
Возрастание и убывание функций Понятие объёма
Понятие объёма Правильные многогранники. Симметрия в пространстве
Правильные многогранники. Симметрия в пространстве Методы решения уравнений
Методы решения уравнений Табличные случаи умножения и деления
Табличные случаи умножения и деления Тройной интеграл
Тройной интеграл Критерий для оптимизации решений в условиях риска и неопределённости
Критерий для оптимизации решений в условиях риска и неопределённости Параллельный перенос
Параллельный перенос Аксиомы стереомотрии
Аксиомы стереомотрии Смешанные числа. Ребус
Смешанные числа. Ребус Игра по ФЭМП средняя группа Выше - ниже
Игра по ФЭМП средняя группа Выше - ниже Умножение 2 и на 2
Умножение 2 и на 2 Вычитание из чисел 6 и 7. Состав 6 и 7
Вычитание из чисел 6 и 7. Состав 6 и 7 Функция y = sin x, ее свойства и график
Функция y = sin x, ее свойства и график