Содержание
- 2. УЧЕБНЫЕ ВОПРОСЫ: 1. Понятие производной функции 2. Основные правила дифференцирования 3. Дифференциал функции 4. Основные теоремы
- 3. Литература 1. «Высшая математика для экономического бакалав-риата: Учебник и практикум» / Под ред. проф. Н.Ш. Кремера.
- 4. Понятие производной функции ПЕРВЫЙ ВОПРОС
- 8. Замечание. Для функции одной переменной дифференцируемость и существование производной – понятия равносильные. Поэтому операцию нахождения производной
- 9. Определение. Если функция y = f (x) имеет производную в каждой точке не-которого промежутка Х (дифференцируема
- 10. Основные правила дифференцирования ВТОРОЙ ВОПРОС
- 19. Дифференциал функции ТРЕТИЙ ВОПРОС
- 20. Замечание. Если f '(x) = 0, то f '(x)∙Δ x не является главной частью прираще-ния Δy,
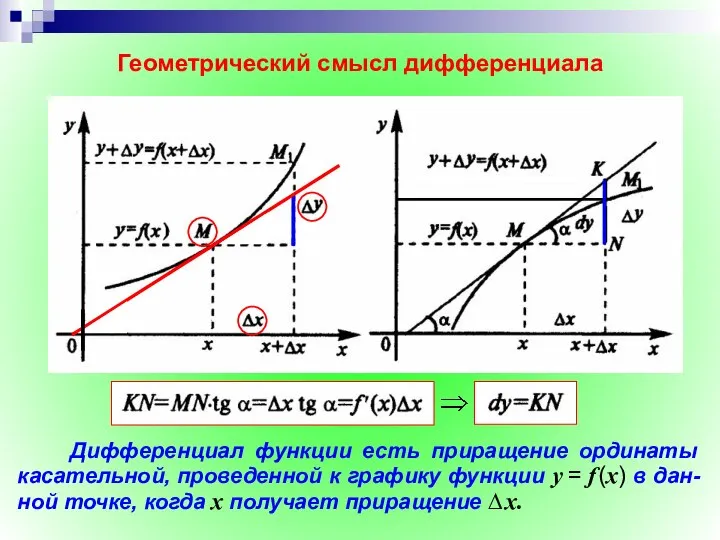
- 21. Геометрический смысл дифференциала Дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f
- 25. Основные теоремы дифференциального исчисления ЧЕТВЕРТЫЙ ВОПРОС
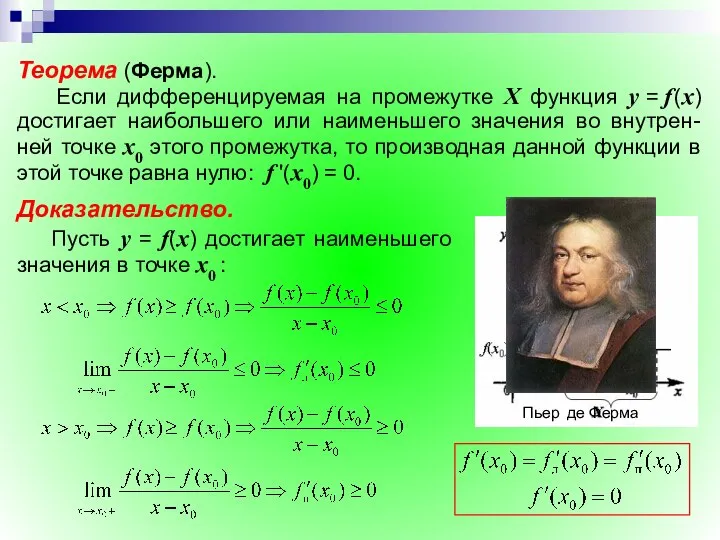
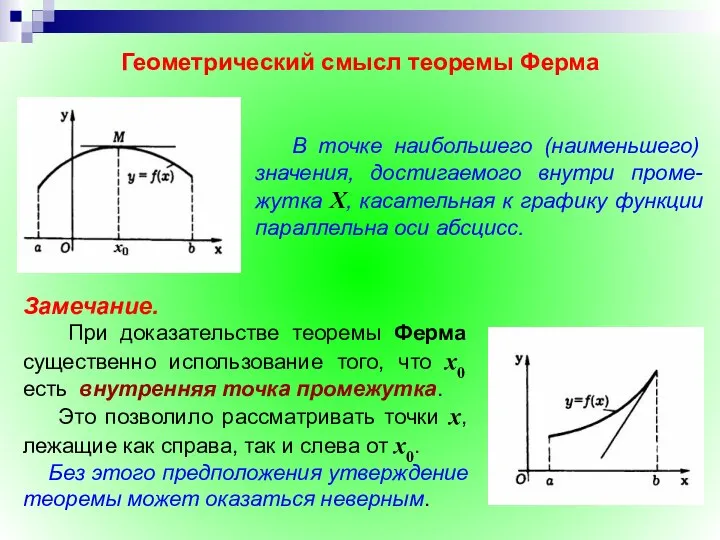
- 26. Теорема (Ферма). Если дифференцируемая на промежутке Х функция y = f (x) достигает наибольшего или наименьшего
- 28. Теорема (Ролля). Пусть функция y = f (x) удовлетворяет следующим условиям: 1) непрерывна на отрезке [а,
- 30. Следствие. Если функция y = f (x) непрерывна на отрезке [а, b] и во всех его
- 31. Замечание. „Элементарное" доказательство теоремы Коши путем двукрат-ного применения к функциям f(x) и g(х) формулы Лагранжа в
- 32. (правило Бернулли – Лопиталя). Правило Бернулли – Лопиталя
- 33. Однако легко видеть
- 35. Скачать презентацию





























 Презентация по математике "Прогрессии вокруг нас" -
Презентация по математике "Прогрессии вокруг нас" -  Таблица умножения и деления на 7 Математический тренажёр
Таблица умножения и деления на 7 Математический тренажёр Logika rozmyta
Logika rozmyta Теорема Менелая. Решение задач
Теорема Менелая. Решение задач Дисперсионный анализ
Дисперсионный анализ Геометрические фигуры
Геометрические фигуры logarifmy_111.pptx_9d08dc30-484f-4528-bf9f-7ed41df5987a (2)
logarifmy_111.pptx_9d08dc30-484f-4528-bf9f-7ed41df5987a (2) Правильные и неправильные дроби
Правильные и неправильные дроби Площади фигур
Площади фигур Теория комплексных чисел. Геометрическая интерпретация комплексного числа. (Тема 3)
Теория комплексных чисел. Геометрическая интерпретация комплексного числа. (Тема 3) Лабораторная работа
Лабораторная работа Осевая симметрия
Осевая симметрия Сумма углов треугольника
Сумма углов треугольника Правило Лопиталя раскрытия неопределенности вида
Правило Лопиталя раскрытия неопределенности вида Простейшие задачи в координатах
Простейшие задачи в координатах Математические цепочки. Устный счет на уроках математики
Математические цепочки. Устный счет на уроках математики Математика в школьных предметах. 6 класс
Математика в школьных предметах. 6 класс Сложение и вычитание десятичных дробей. Обобщающий урок
Сложение и вычитание десятичных дробей. Обобщающий урок Кривые второго порядка
Кривые второго порядка Метрология, стандартизация и сертификация
Метрология, стандартизация и сертификация Симметрия в пространстве
Симметрия в пространстве Умножение натуральных чисел
Умножение натуральных чисел Планирование экспериментов применительно к объекту исследований
Планирование экспериментов применительно к объекту исследований Числовые и буквенные выражения
Числовые и буквенные выражения Подготовка к ВПР (№1). Математика 6 класс
Подготовка к ВПР (№1). Математика 6 класс Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов Понятие матрицы
Понятие матрицы Презентация по математике "Линейная функция и её график" - скачать
Презентация по математике "Линейная функция и её график" - скачать