Содержание
- 2. Logika rozmyta Logika rozmyta wprowadza obliczoną wartość średnią między absolutną prawdą i absolutnym fałszem z rezultatem
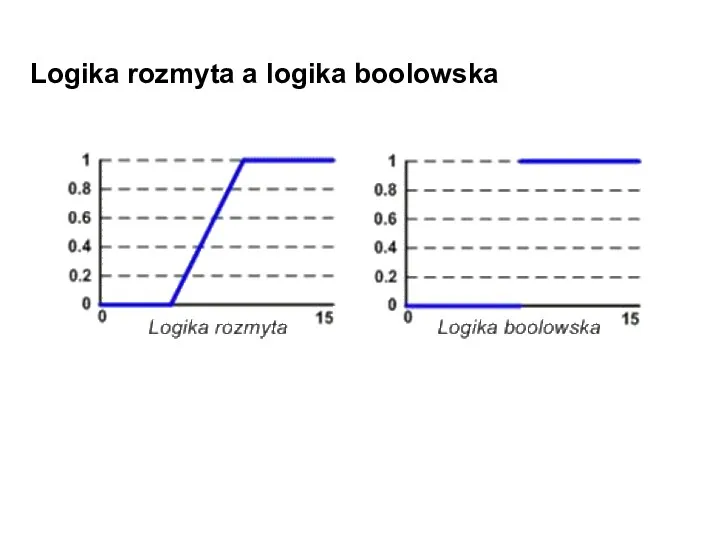
- 3. Logika rozmyta a logika boolowska
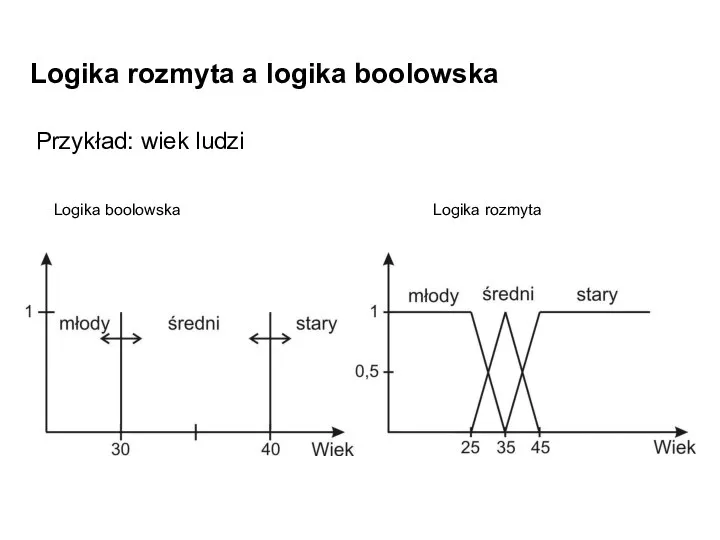
- 4. Logika rozmyta a logika boolowska Przykład: wiek ludzi Logika boolowska Logika rozmyta
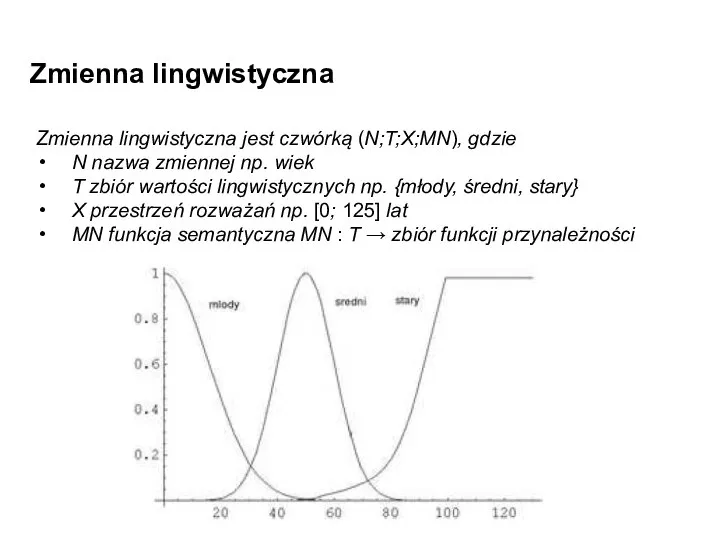
- 5. Zmienna lingwistyczna Zmienna lingwistyczna jest czwórką (N;T;X;MN), gdzie N nazwa zmiennej np. wiek T zbiór wartości
- 6. Zbiory rozmyte Należy ustalić obszar rozważań X nazywany przestrzenią – zakres zmian rozważanych wielkości Zbiorem rozmytym
- 7. Zbiory rozmyte – zapis symboliczny Elementami zbioru X mogą być nie tylko liczby, ale również inne
- 8. Zbiory rozmyte Funkcja przynależności każdemu elementowi x przypisuje jego stopień przynależności do zbioru rozmytego A, przy
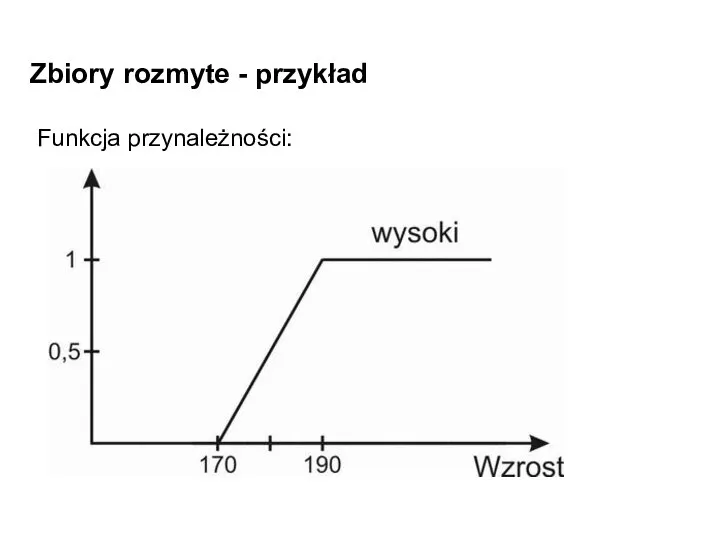
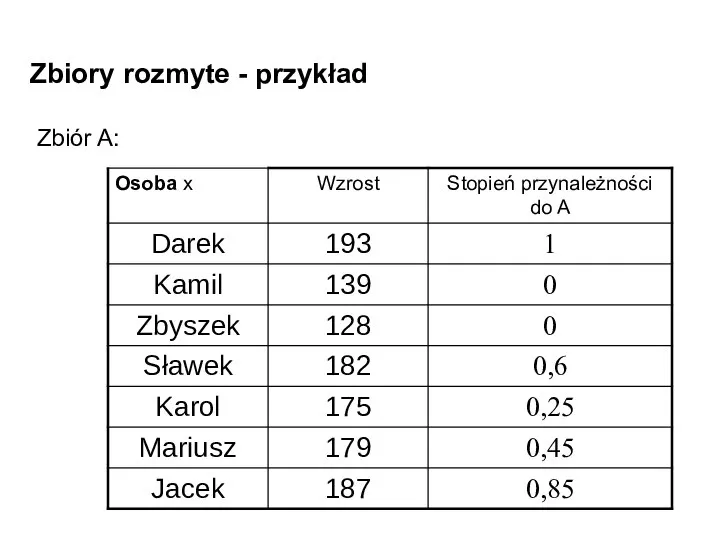
- 9. Zbiory rozmyte - przykład Niech naszym zbiorem X będą osoby, a zbiorem rozmytym A osoby wysokie.
- 10. Zbiory rozmyte - przykład Funkcja przynależności:
- 11. Zbiory rozmyte - przykład Zbiór A:
- 12. Zbiory rozmyte - przykład Zbiór A: A={(Darek,1);(Kamil,0);(Zbyszek,0);(Sławek,0.6);(Karol;0.25);(Mariusz,0.45);(Jacek,0.85)}
- 13. Zbiory rozmyte - definicje Wysokość zbioru rozmytego A oznaczamy przez h(A) i określamy jako: W przypadku
- 14. Zbiory rozmyte - definicje Normalnym nazywamy zbiór rozmyty wtedy i tylko wtedy, gdy h(A) = 1.
- 15. Zbiory rozmyte - definicje Zbiór rozmyty A jest równy zbiorowi rozmytemu B, co zapisujemy A =
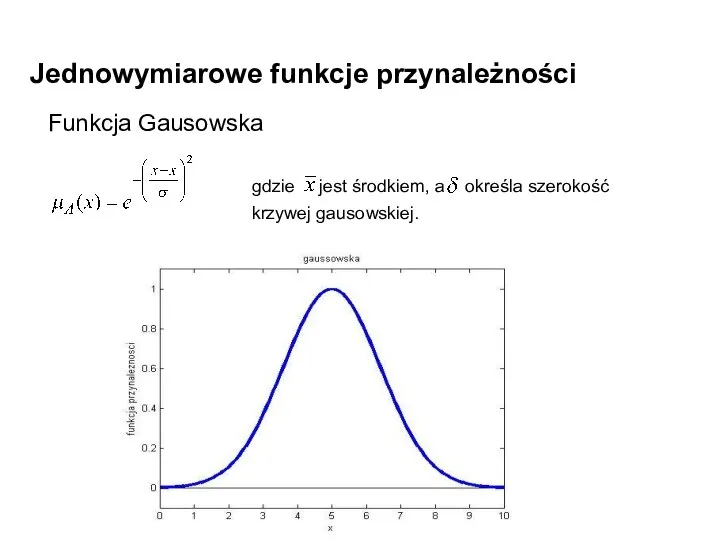
- 16. Jednowymiarowe funkcje przynależności Funkcja Gausowska gdzie jest środkiem, a określa szerokość krzywej gausowskiej.
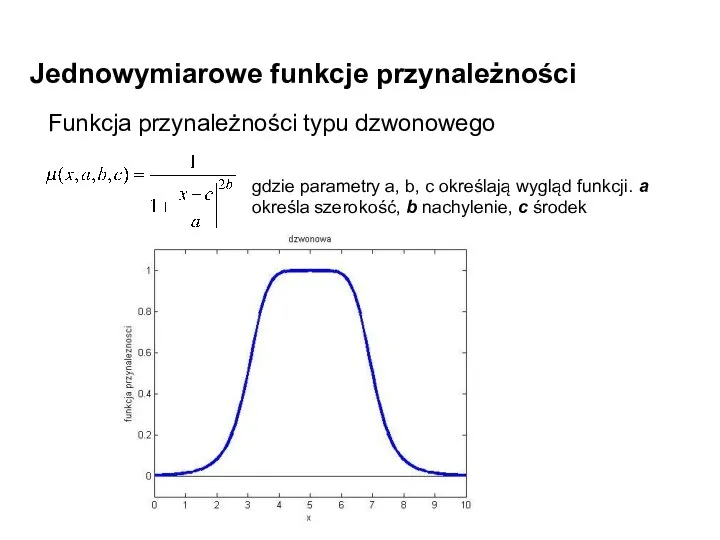
- 17. Jednowymiarowe funkcje przynależności Funkcja przynależności typu dzwonowego gdzie parametry a, b, c określają wygląd funkcji. a
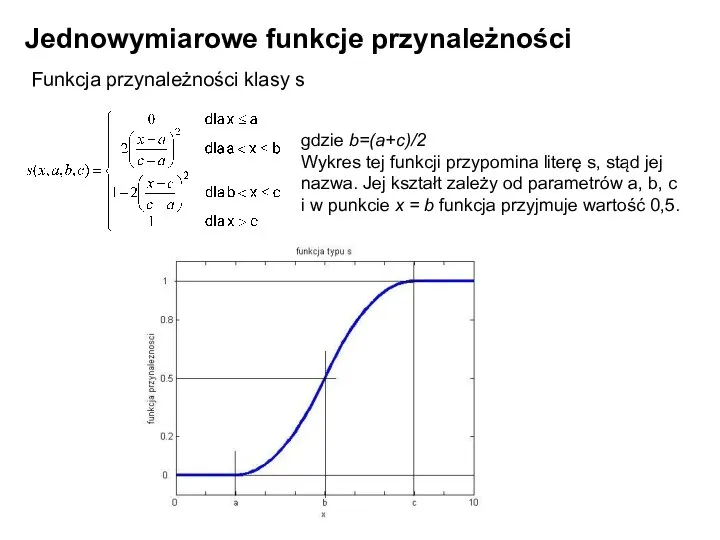
- 18. Jednowymiarowe funkcje przynależności Funkcja przynależności klasy s gdzie b=(a+c)/2 Wykres tej funkcji przypomina literę s, stąd
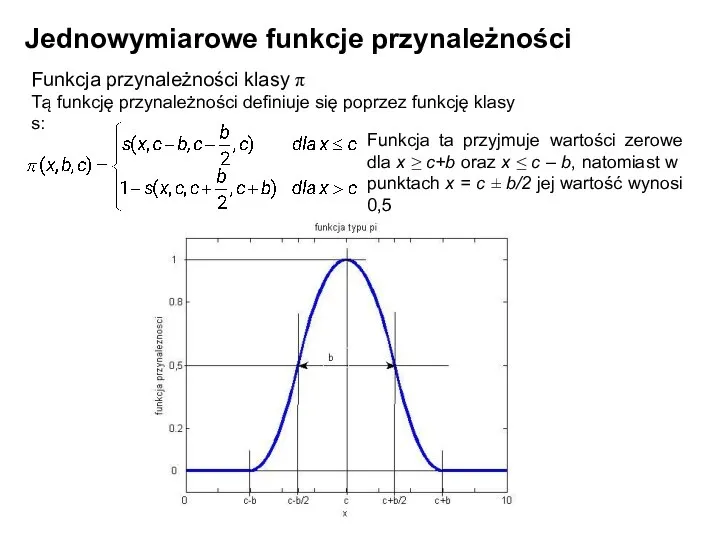
- 19. Jednowymiarowe funkcje przynależności Funkcja przynależności klasy π Tą funkcję przynależności definiuje się poprzez funkcję klasy s:
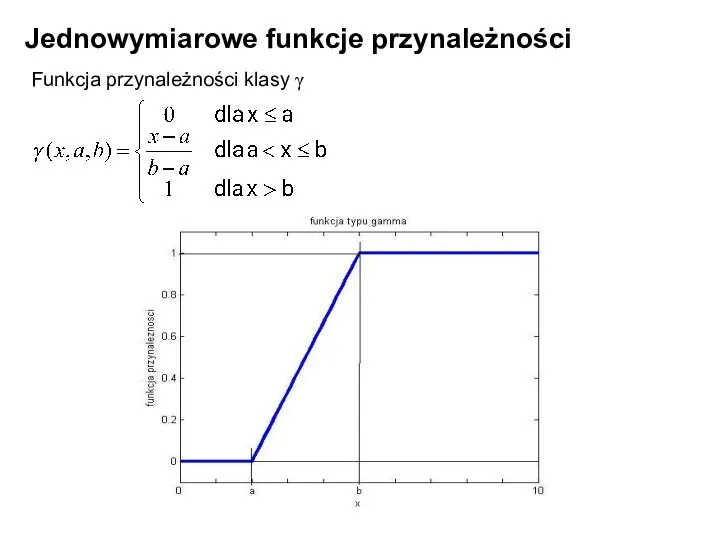
- 20. Jednowymiarowe funkcje przynależności Funkcja przynależności klasy γ
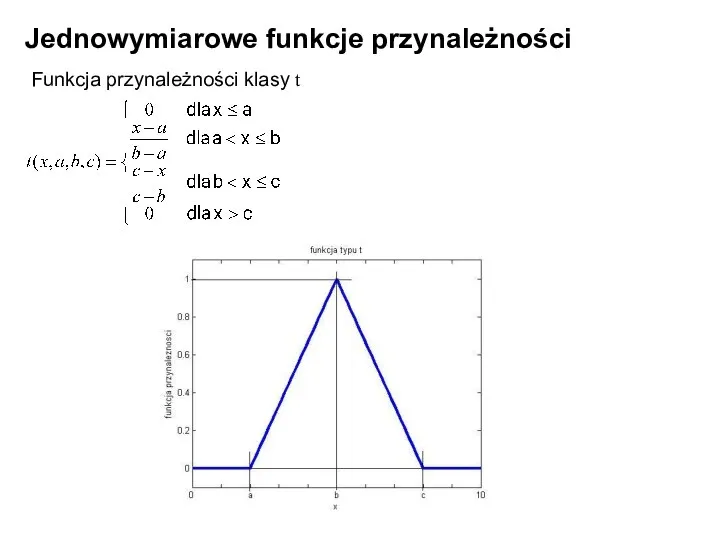
- 21. Jednowymiarowe funkcje przynależności Funkcja przynależności klasy t
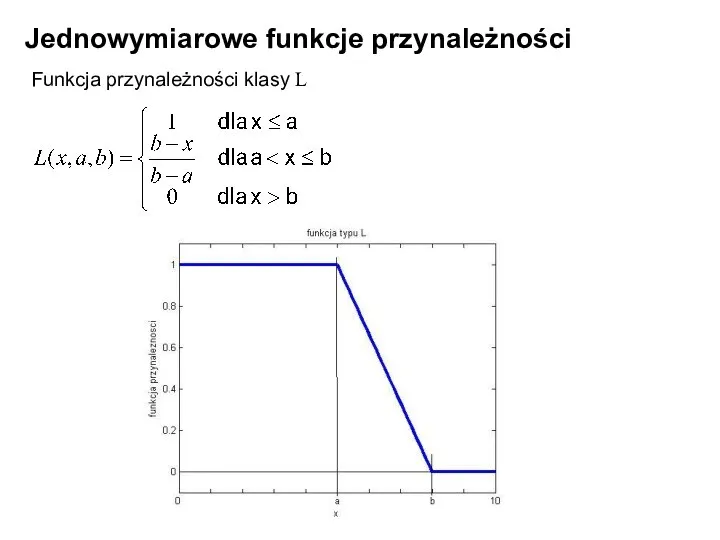
- 22. Jednowymiarowe funkcje przynależności Funkcja przynależności klasy L
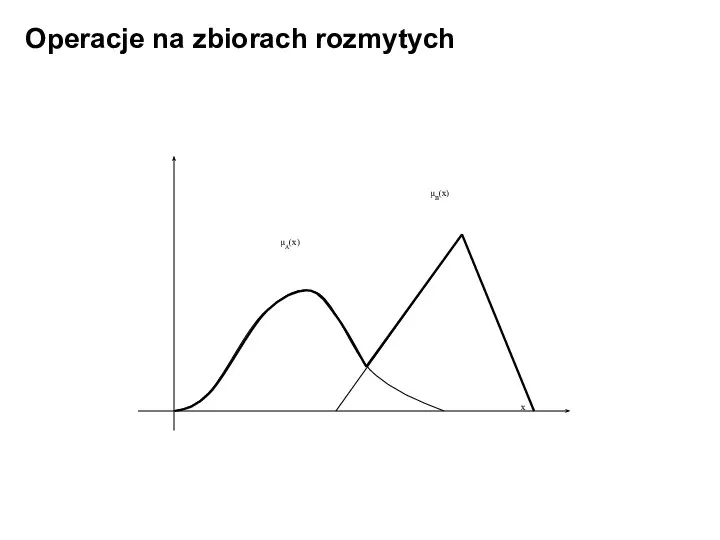
- 23. Operacje na zbiorach rozmytych Sumą zbiorów rozmytych A i B jest zbiór rozmyty A ∪ B
- 24. Operacje na zbiorach rozmytych
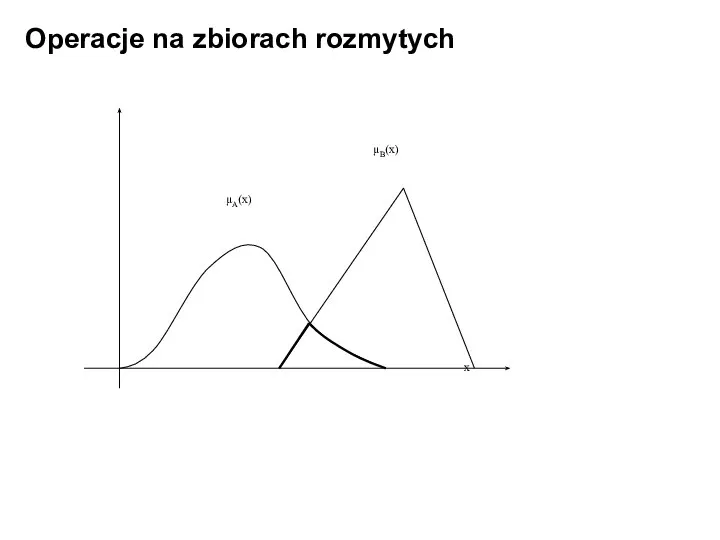
- 25. Operacje na zbiorach rozmytych Przecięciem zbiorów rozmytych A, B ⊆ X jest zbiór rozmyty A ∩
- 26. Operacje na zbiorach rozmytych
- 28. Скачать презентацию











 Производная функции
Производная функции Планета Математика
Планета Математика Выборочное наблюдение
Выборочное наблюдение Свойства сложения
Свойства сложения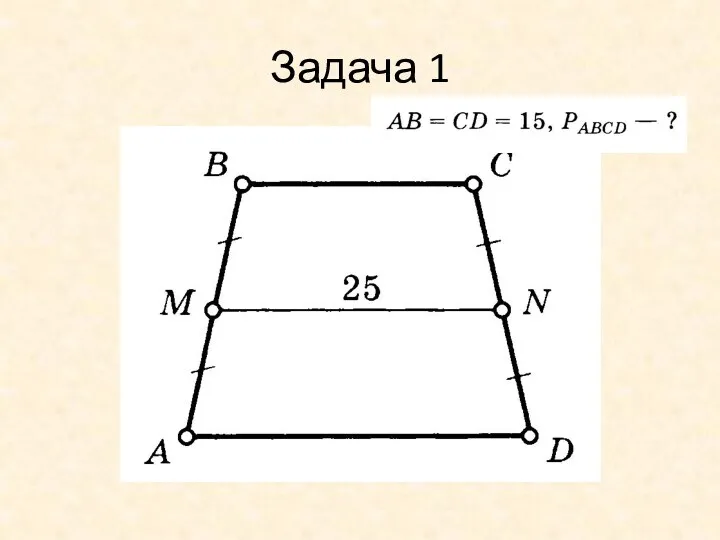 Задачи №№ 1- 8
Задачи №№ 1- 8 Путешествие в страну треугольников
Путешествие в страну треугольников График квадратичной функции. Построение графика квадратичной функци
График квадратичной функции. Построение графика квадратичной функци Решение логических задач на уроках математики
Решение логических задач на уроках математики Загадка картины Н.П. Богданова-Бельского «Трудная задача»
Загадка картины Н.П. Богданова-Бельского «Трудная задача» Понятие многогранника. Призма
Понятие многогранника. Призма Неопределённый интеграл. Метод подстановки (замены переменной)
Неопределённый интеграл. Метод подстановки (замены переменной) Признаки подобия треугольников (урок-практикум)
Признаки подобия треугольников (урок-практикум) Теорема Виета
Теорема Виета Распределение простых чисел
Распределение простых чисел Роль диагностики в обучении математи
Роль диагностики в обучении математи Обобщающий урок по теме «Соотношения между сторонами и углами треугольника»
Обобщающий урок по теме «Соотношения между сторонами и углами треугольника» Правильные многогранники
Правильные многогранники Построение графика квадлатичной функции
Построение графика квадлатичной функции Решение текстовых задач с помощью систем линейных уравнений
Решение текстовых задач с помощью систем линейных уравнений Преобразование фигур. 9 класс
Преобразование фигур. 9 класс Презентация по математике "История алгебры" - скачать
Презентация по математике "История алгебры" - скачать  Параллелограмм
Параллелограмм Показатели вариации
Показатели вариации Равнобедренный треугольник. Прямоугольник. Параллелограмм ,не являющийся прямоугольником. Равновеликие фигуры
Равнобедренный треугольник. Прямоугольник. Параллелограмм ,не являющийся прямоугольником. Равновеликие фигуры Векторы
Векторы Признаки делимости на 10, на 5, на 2
Признаки делимости на 10, на 5, на 2 Элементы математической статистики и теории вероятности
Элементы математической статистики и теории вероятности Проект - игра " Увлекательное путешествие в страну МиФ"
Проект - игра " Увлекательное путешествие в страну МиФ"