Содержание
- 2. Майер И.И. 3.1. Первообразная. Неопределенный интеграл. Основные понятия Определения
- 3. Майер И.И. Первообразная. Неопределенный интеграл. Пусть задана дифференцируемая функция F(x). Определим ее первую производную, функцию f(x),
- 4. Майер И.И. Первообразная. Неопределенный интеграл. Пример. Пусть задана функция F(x)=x3. Очевидно, она является первообразной функции f(x)=3x2
- 5. Майер И.И. Первообразная. Неопределенный интеграл (продолжение) Справедливо утверждение: Если функция F(x) - первообразная функции f(x) на
- 6. Майер И.И. Так как то Следовательно, если функцию f(x) проинтегрировать, а затем полученный результат продифференцировать, то
- 7. Майер И.И. 3.2. Основные методы интегрирования Таблица интегралов Методы вычисления неопределенных интегралов
- 8. Майер И.И. Основные методы интегрирования Вычисление неопределенного интеграла - задача значительно более сложная, чем отыскание производной.
- 9. Майер И.И. Таблица основных интегралов, с - константа 1. с - константа 2. 3. 4. 5.
- 10. Майер И.И. 8. 9. 10. 11. 12.
- 11. Майер И.И. Методы вычисления неопределенных интегралов. В рамках изучаемой дисциплины рассматриваются следующие методы вычисления неопределенных интегралов:
- 12. Майер И.И. 1. Метод преобразования подынтегрального выражения (подынтегральной функции) Пример 1.1. Вычислить Решение. Преобразованием подынтегральной функции
- 13. Майер И.И. 1. Метод преобразования подынтегрального выражения (подынтегральной функции) Пример 1.2. Вычислить Решение. Преобразуем подынтегральную функцию
- 14. Майер И.И. 2. Ввод новой переменной интегрирования. Вместо переменной интегрирования x вводят новую Переменную интегрирования t
- 15. Майер И.И. 2. Ввод новой переменной интегрирования. Пример 2.1. Вычислить Решение. Введем новую переменную t=1-3x. Продифференцируем
- 16. Майер И.И. Пример 2.2. Вычислить интеграл Решение. Сделаем замену переменной t=4x+2. Тогда
- 17. Майер И.И. Пример 2.3. Вычислить Решение. Введем новую переменную t=x2 Тогда
- 18. Майер И.И. 3. Метод интегрирования по частям. Дан интеграл где подынтегральное выражение представляет собой произведение некоторой
- 19. Майер И.И. Пример 3.1. Найти Решение. Пусть Чтобы применить формулу интегрирования по частям найдем du и
- 20. Майер И.И. Пример 3.2. Найти Решение. Пусть Тогда Применив формулу интегрирования по частям, получим
- 21. Майер И.И. 4. Метод интегрирования рациональных функций Рациональной функцией или рациональной дробью называется функция которая равна
- 22. Майер И.И. Пример 4.1. Найти Решение. Разобьем сначала интеграл на сумму двух интегралов, из которых первый
- 23. Майер И.И. Пример 4.2 Найти Решение. Подынтегральная функция не является правильной дробью. Преобразуем подынтегральное выражение
- 24. Майер И.И. Пример 4.3. Найти Решение. Представим подынтегральную функцию как сумму простейших дробей: Приведем правую часть
- 25. Майер И.И. 3.3. Определенный интеграл Задача о площади. Определенный интеграл –основные понятия
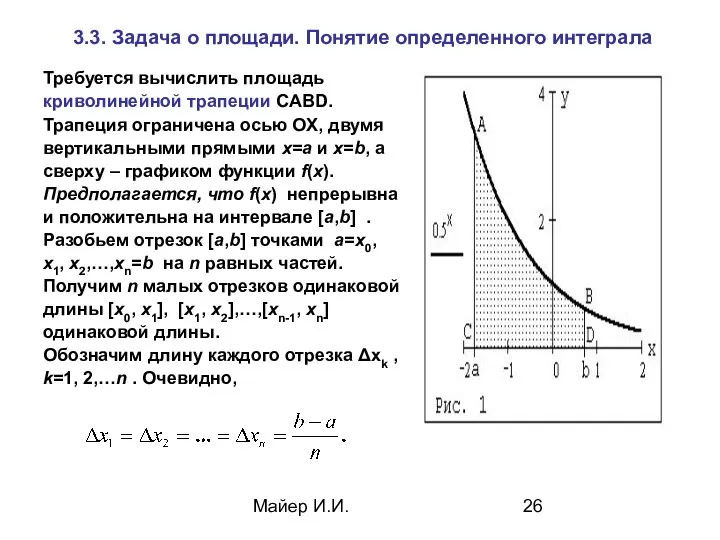
- 26. Майер И.И. 3.3. Задача о площади. Понятие определенного интеграла Требуется вычислить площадь криволинейной трапеции CABD. Трапеция
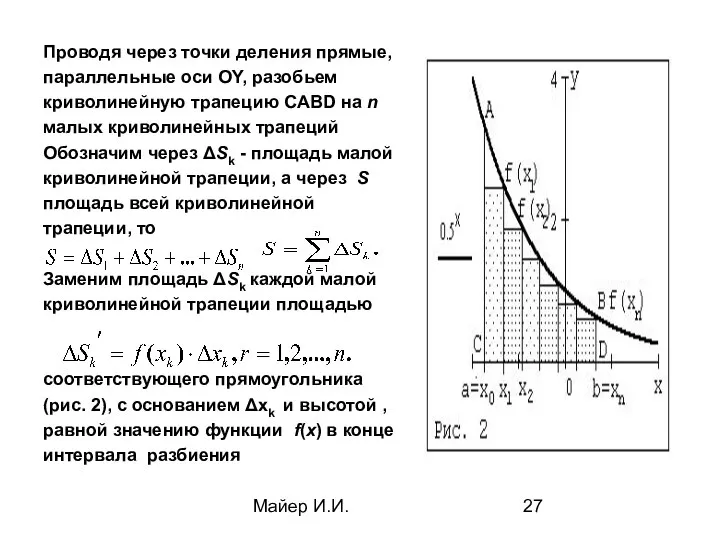
- 27. Майер И.И. Проводя через точки деления прямые, параллельные оси OY, разобьем криволинейную трапецию CABD на n
- 28. Майер И.И. Очевидно, что и искомую площадь можно приближенно представить суммой площадей прямоугольников, что равносильно замене
- 29. Майер И.И. Сумма вида называется интегральной суммой Предел, к которому стремится последовательность интегральных сумм при n→∞
- 30. Майер И.И. В записи определенного интеграла числа a и b - соответственно нижний и верхний пределы
- 31. Майер И.И. 3.4. Вычисление определенного интеграла. Основные свойства
- 32. Майер И.И. Для вычисления определенного интеграла применяют формулу Ньютона-Лейбница: Эта формула справедлива, если f(x) непрерывна на
- 33. Майер И.И. Основные свойства определенного интеграла 1. 2. 3. 4. Если интервал интегрирования [a, b] разбит
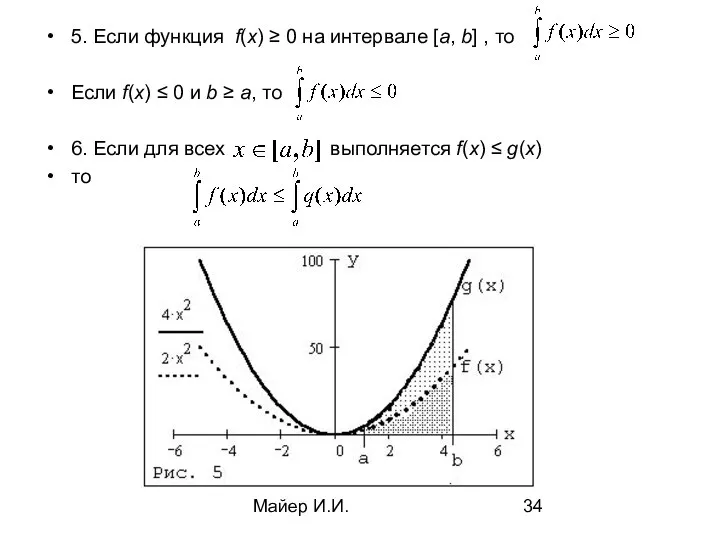
- 34. Майер И.И. 5. Если функция f(x) ≥ 0 на интервале [a, b] , то Если f(x)
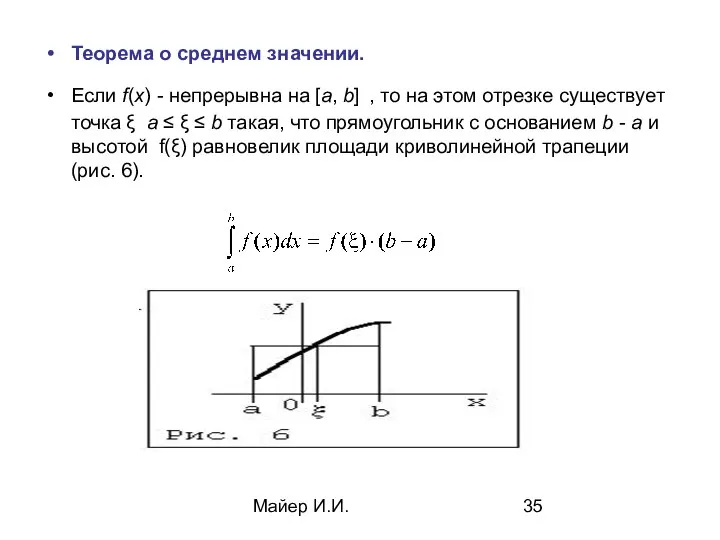
- 35. Майер И.И. Теорема о среднем значении. Если f(x) - непрерывна на [a, b] , то на
- 36. Майер И.И. Примеры вычисления определенного интеграла
- 37. Майер И.И. Пример 1. Вычислить Решение. Воспользуемся методом замены переменной. Обозначим , тогда При вычислении определенного
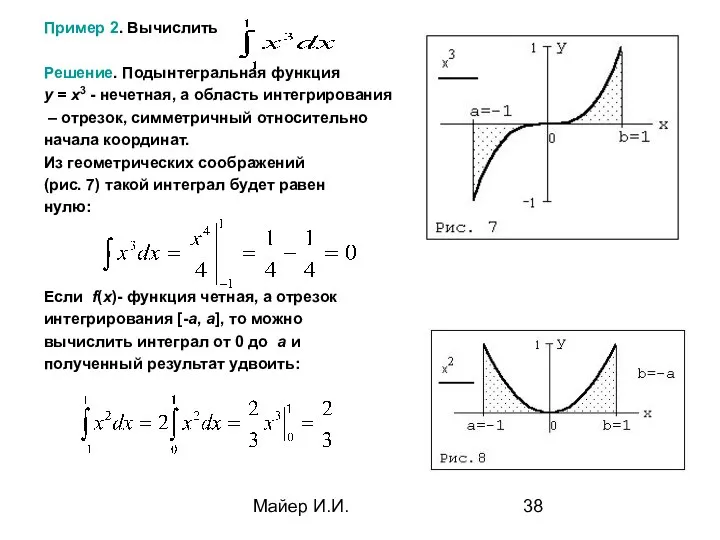
- 38. Майер И.И. Пример 2. Вычислить Решение. Подынтегральная функция y = x3 - нечетная, а область интегрирования
- 39. Майер И.И. Пример 3. Вычислить Решение. Воспользуемся формулой интегрирования по частям Возьмем в качестве Тогда
- 40. Майер И.И. 3.5. Несобственные интегралы Определение термина «Определенный интеграл» было дано в предположении, что промежуток интегрирования
- 41. Майер И.И. Пример. Функция непрерывна на бесконечном интервале . Если A - любое конечное число, A
- 43. Скачать презентацию


































 Столбчатые диаграммы и графики
Столбчатые диаграммы и графики Сложение и вычитание многозначных чисел. Закрепление. Деловая игра. 4 класс
Сложение и вычитание многозначных чисел. Закрепление. Деловая игра. 4 класс Группировки в историческом исследовании. (Лекция 2)
Группировки в историческом исследовании. (Лекция 2) Сложение и вычитание многозначных чисел
Сложение и вычитание многозначных чисел  Inscribed and circumscribed circles of a triangle
Inscribed and circumscribed circles of a triangle Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Задачи на построение
Задачи на построение Обработка многократно измеренных величин
Обработка многократно измеренных величин Моделирование алгоритмов вейвлет-преобразования. Матрица гармонического вейвлет-преобразования
Моделирование алгоритмов вейвлет-преобразования. Матрица гармонического вейвлет-преобразования Презентация на тему Обозначение натуральных чисел 5 класс
Презентация на тему Обозначение натуральных чисел 5 класс Решение дробных рациональных уравнений. 8 класс
Решение дробных рациональных уравнений. 8 класс Первообразная и интеграл
Первообразная и интеграл Приближенное вычисление интегралов (тема 9)
Приближенное вычисление интегралов (тема 9) Построение треугольника по трем элементам
Построение треугольника по трем элементам Развитие пространственного мышления с опорой на наглядно-образное мышление. Разрезные фигуры
Развитие пространственного мышления с опорой на наглядно-образное мышление. Разрезные фигуры Презентация по математике "Метод математической индукции" - скачать бесплатно
Презентация по математике "Метод математической индукции" - скачать бесплатно Математическая викторина
Математическая викторина Урок геометрии 8 класс
Урок геометрии 8 класс Мәйданнарны үлчәү берәмлекләре
Мәйданнарны үлчәү берәмлекләре Число π (пи)
Число π (пи) Числа 1 – 5 закрепление
Числа 1 – 5 закрепление Прибавить и вычесть число 1
Прибавить и вычесть число 1 Решение практико-ориентированных задач
Решение практико-ориентированных задач Наши истинные учителя опыт и чувства. Из истории геометрии
Наши истинные учителя опыт и чувства. Из истории геометрии Математика XIX ст. Жан Батист Жозеф Фур'є
Математика XIX ст. Жан Батист Жозеф Фур'є Скорость движения
Скорость движения Числовые последовательности
Числовые последовательности Основные понятия алгебры логики
Основные понятия алгебры логики