Элементы линейной алгебры

Матрицы

Матрицей размера m×n называется прямоугольная таблица чисел, состоящая из m строк и n

Виды матриц. Квадратная матрица (m=n)

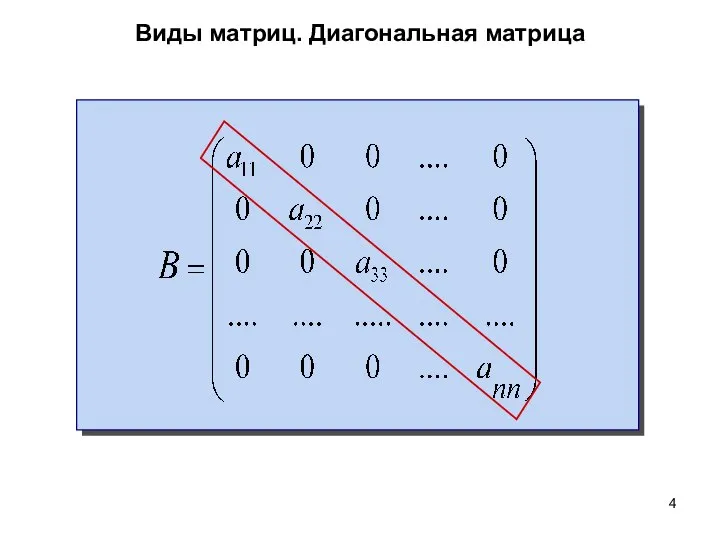
Виды матриц. Диагональная матрица

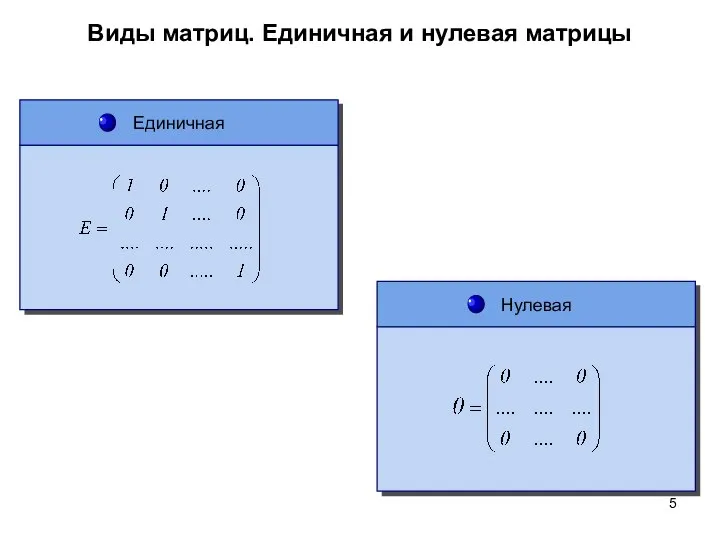
Виды матриц. Единичная и нулевая матрицы

Нулевая

Единичная

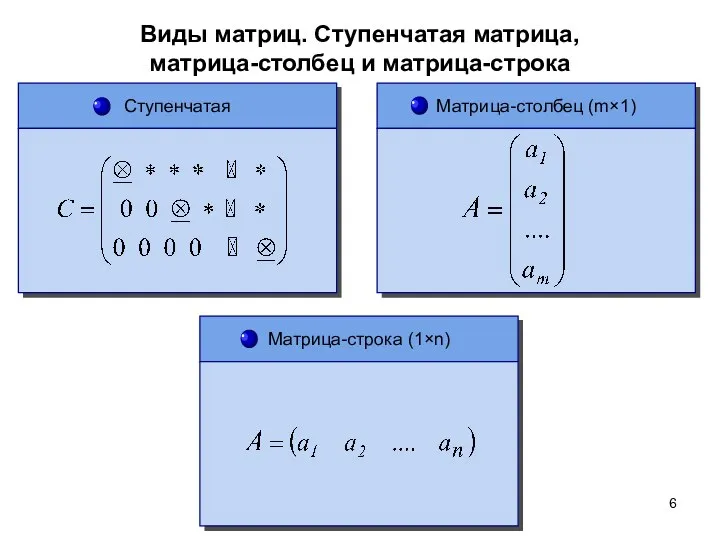
Виды матриц. Ступенчатая матрица, матрица-столбец и матрица-строка

Ступенчатая

Матрица-строка (1×n)

Матрица-столбец (m×1)

Равенство матриц

1) Размеры матриц совпадают

2) Соответствующие элементы матриц равны:
aij=bij,
i=1,m; j=1,n.

Две матрицы
A= (aij) и B=(bij) называются равными, если

Сумма матриц

Пример.

Суммой матриц A=(aij) и B=(bij) одинакового размера m×n называется матрица C=(cij)

Разность матриц

Пример.

Разностью матриц A=(aij) и B=(bij) одинакового размера m×n называется матрица C=(cij)

Произведение матрицы на число

Произведением матрицы A=(aij) на число λ называется матрица того

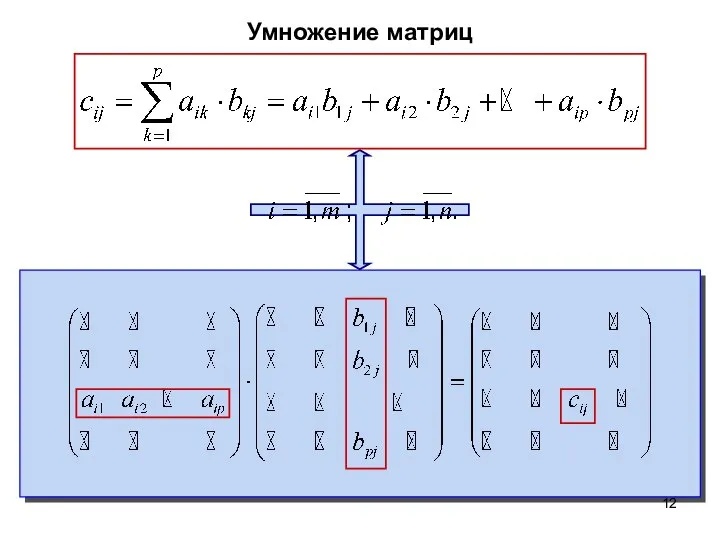
Умножение матриц

Произведением матрицы A=(aij) (размера m×p) на матрицу B=(bij) (размера p×n) называется матрица

Умножение матриц

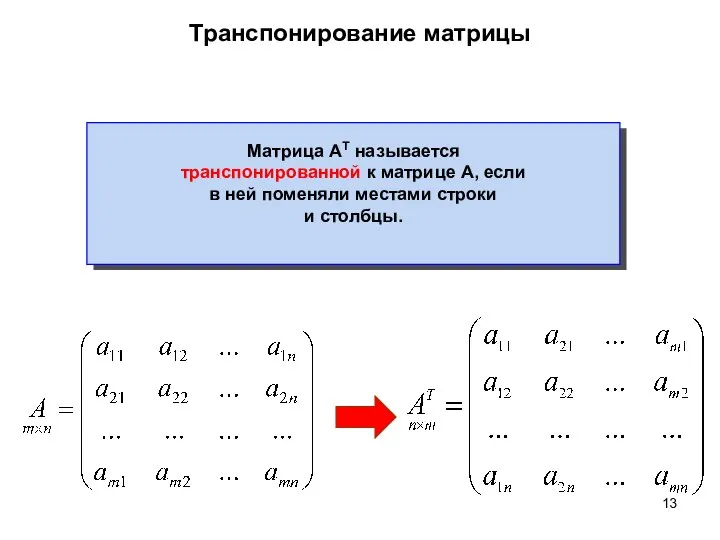
Транспонирование матрицы

Матрица АТ называется
транспонированной к матрице А, если
в ней

Определитель матрицы

Определитель – это число,
характеризующее квадратную
матрицу.

1.

2.

3.

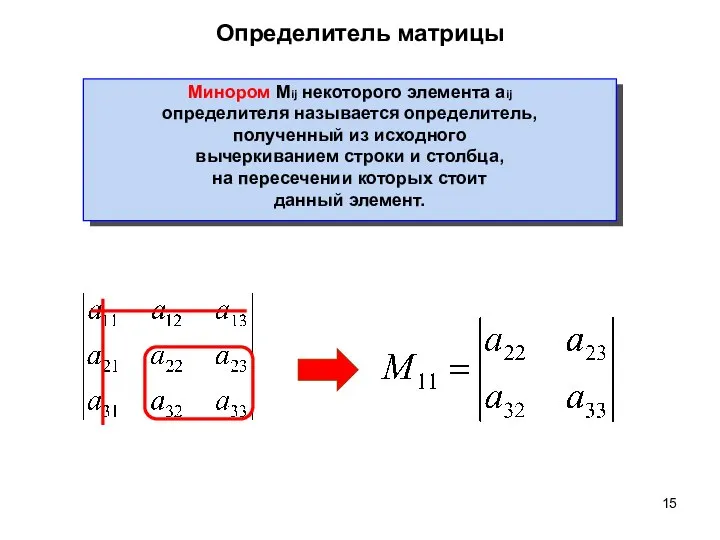
Определитель матрицы

Минором Mij некоторого элемента aij
определителя называется определитель,
полученный из

Определитель матрицы

Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный

Обратная матрица

Пусть дана невырожденная (det A≠0) квадратная матрица порядка n

Матрица А-1 называется

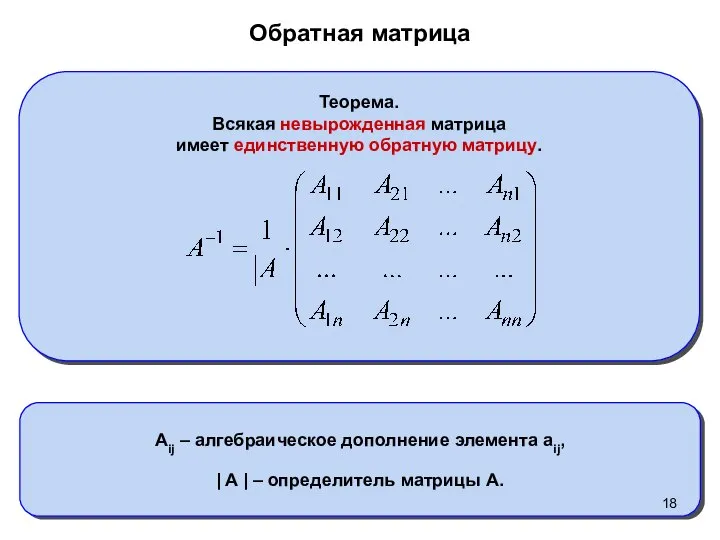
Обратная матрица

Теорема.
Всякая невырожденная матрица имеет единственную обратную матрицу.

Aij – алгебраическое дополнение элемента

Системы линейных уравнений

Системой m линейных уравнений с n неизвестными называется система вида

где

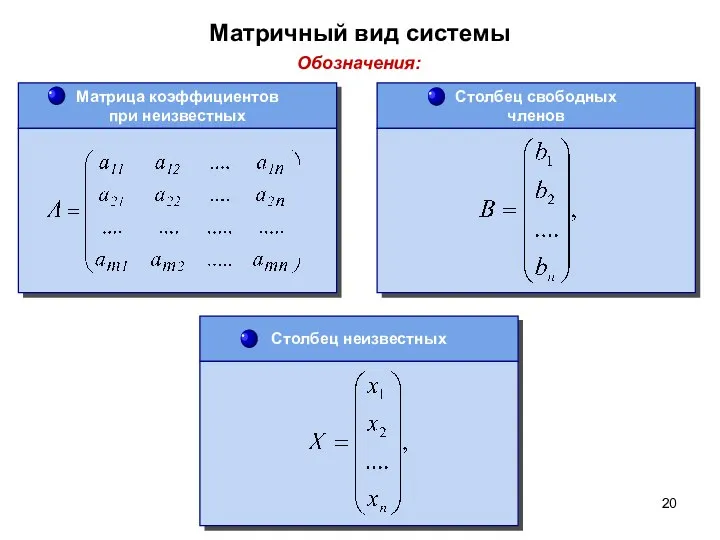
Матричный вид системы

Обозначения:

Матрица коэффициентов при неизвестных

Столбец неизвестных

Столбец свободных членов

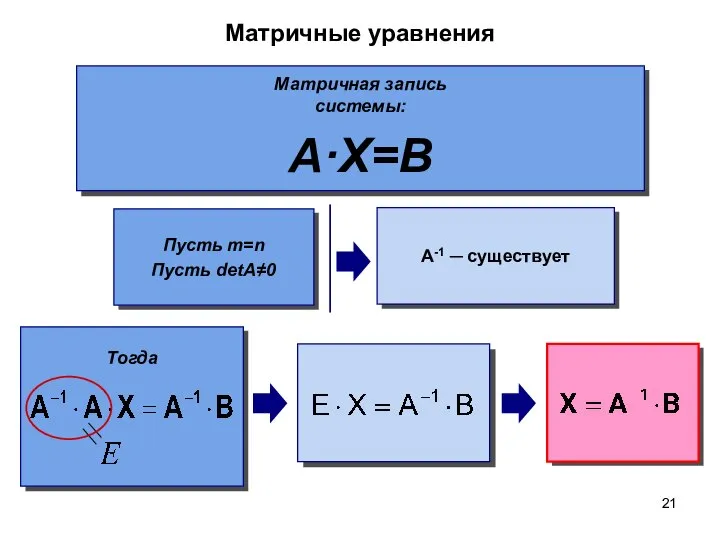
Матричные уравнения

Матричная запись системы:
A·X=B

A-1 ─ существует

Пусть m=n
Пусть detA≠0

Тогда

Правило Крамера

Пусть m=n
Пусть detA = Δ ≠ 0

Рассмотрим систему

J – столбец

Обозначим

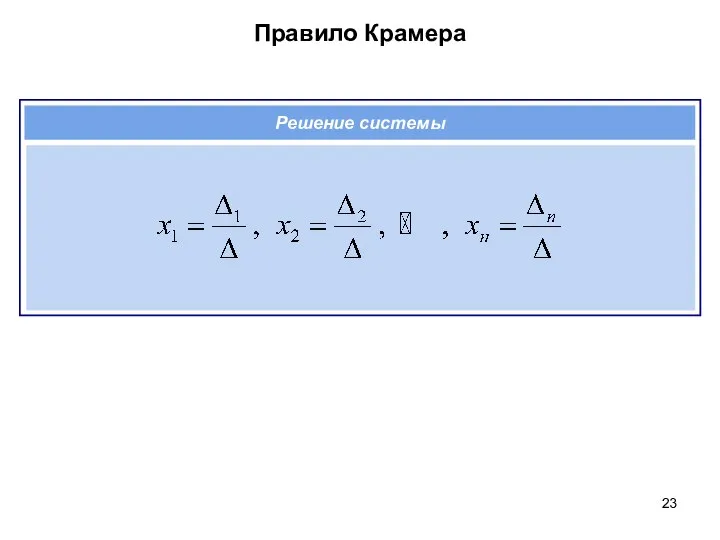
Правило Крамера

Решение системы

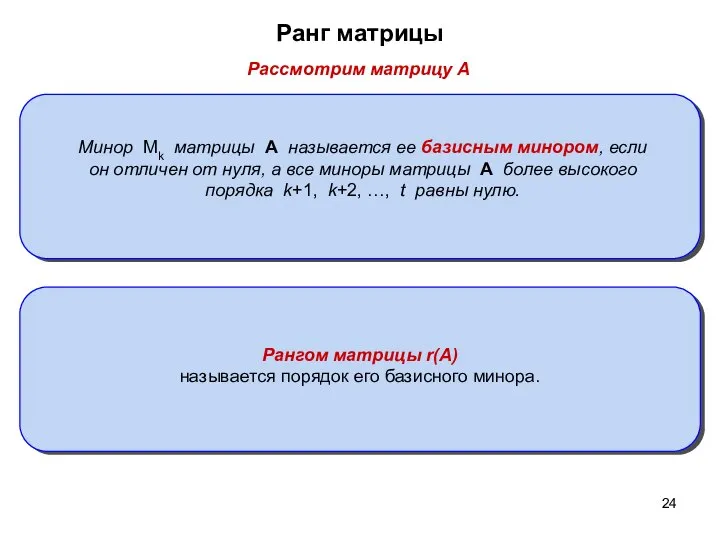
Ранг матрицы

Рассмотрим матрицу A
Рангом матрицы r(A) называется порядок его базисного минора.
Минор Mk

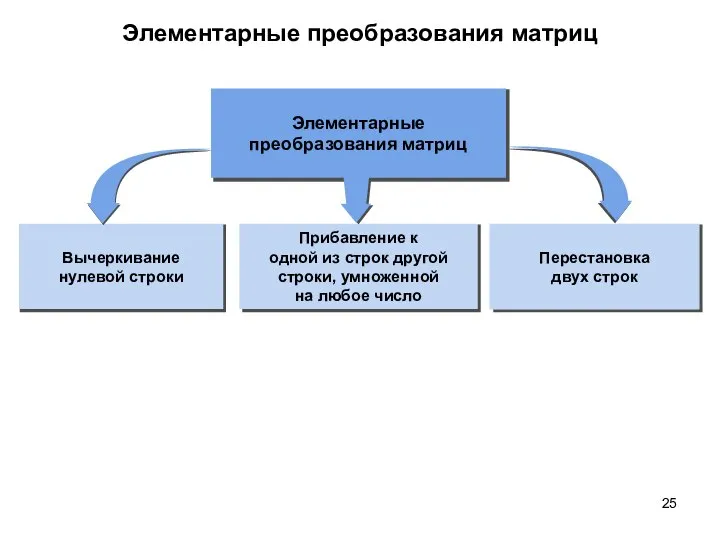
Элементарные преобразования матриц

Вычеркивание нулевой строки

Элементарные преобразования матриц

Перестановка двух строк

Прибавление к одной из строк другой строки,

Элементарные преобразования матриц

Теорема 1.
Любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.
Теорема

Метод Гаусса
Метод последовательного исключения неизвестных – наиболее распространенный метод решения систем линейных уравнений.
Суть

Метод Гаусса

Рассмотрим систему

С помощью элементарных преобразований приводим ее к равносильной системе ступенчатого

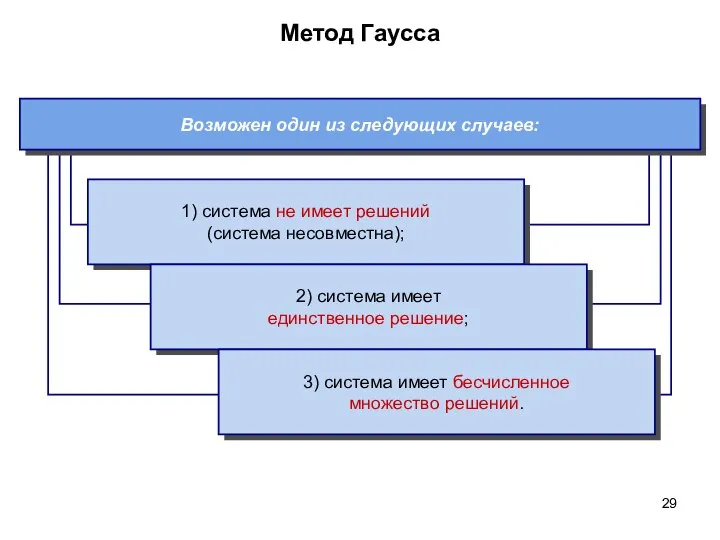
Метод Гаусса

Возможен один из следующих случаев:

1) система не имеет решений (система несовместна);

2)

Теорема Кронекера-Капелли

Рассмотрим систему уравнений

Обозначим