Содержание
- 2. СОДЕРЖАНИЕ: Теория графов. История возникновения. Что же такое граф? Связность. Теоремы о связности. Задача о кёнигсбергских
- 3. ТЕОРИЯ ГРАФОВ - это область дискретной математики, особенностью которой является геометрический подход к изучению объектов. Теория
- 4. ИСТОРИЯ ВОЗНИКНОВЕНИЯ ТЕОРИИ Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих
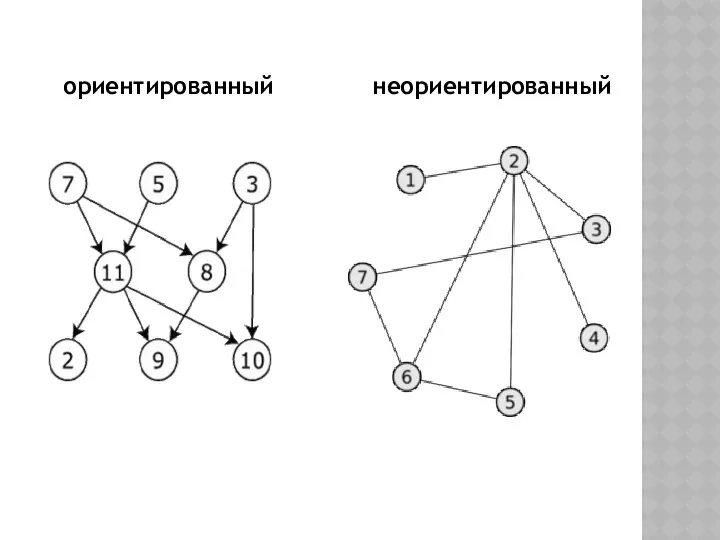
- 5. ЧТО ЖЕ ТАКОЕ ГРАФ? Граф G = есть совокупность множества вершин V и множества рёбер (дуг)
- 6. ориентированный неориентированный
- 7. СВЯЗНОСТЬ Пусть граф G — неориентированный. Две вершины a и b называются связанными, если существует путь
- 8. ТЕОРЕМЫ О СВЯЗНОСТИ. Если в конечном неориентированном простом графе G ровно две вершины a и b
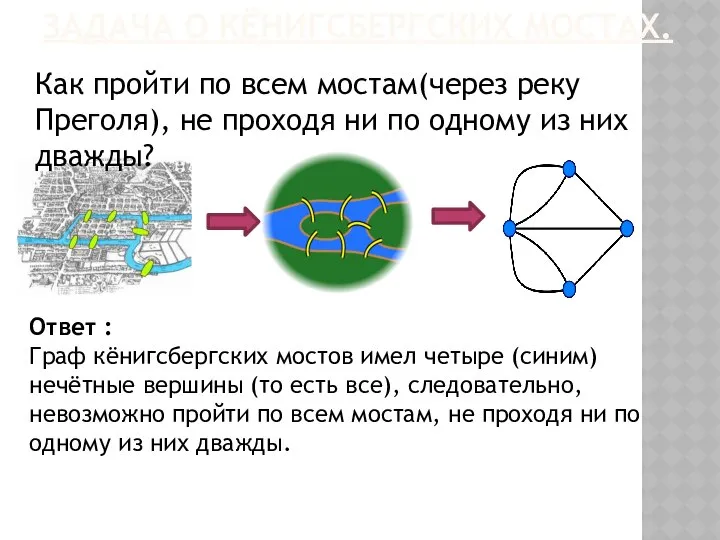
- 9. ЗАДАЧА О КЁНИГСБЕРГСКИХ МОСТАХ. Как пройти по всем мостам(через реку Преголя), не проходя ни по одному
- 10. ВЫВОДЫ ЭЙЛЕРА: Число нечётных вершин графа должно быть чётно. Не может существовать граф, который имел бы
- 11. ПРИМЕРЫ ЗАДАЧ: Задача 1. Лист бумаги Плюшкин (Н.В.Гоголь "Мертвые души") разрезает на три части. Некоторые из
- 12. Задача 2. Утверждают, что в одной компании из пяти человек каждый знаком с двумя другими. Возможна
- 13. . ДЕРЕВЬЯ Связные графы, в которых существует одна и только одна цепь, соединяющая каждую пару вершин,
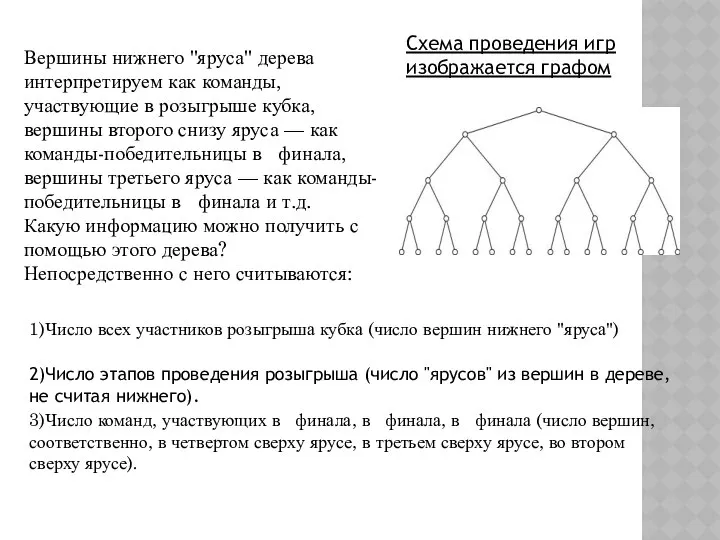
- 14. Схема проведения игр изображается графом Вершины нижнего "яруса" дерева интерпретируем как команды, участвующие в розыгрыше кубка,
- 15. Примечание. Список используемой литературы. http://textarchive.ru/c-1728339-pall.html https://www.hse.ru/data/2010/10/14/1223122510/DA_Teor_Graph.pdf http://www.math.mrsu.ru/text/courses/method/osn_pon_teor_graph.htm http://ougeorg.kormil.obr55.ru/matem2.doc http://dfgm.math.msu.su/files/0ngit/shafarevich/lecture1.pdf
- 17. Скачать презентацию











 Математическая сказка о Зайчике
Математическая сказка о Зайчике Вынесение множителя из-под знака корня. Внесение множителя под знак корня. 8 класс
Вынесение множителя из-под знака корня. Внесение множителя под знак корня. 8 класс Цилиндр. Конус. Шар
Цилиндр. Конус. Шар УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ. 6 класс. Занятие 9.
УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ. 6 класс. Занятие 9. Презентация по математике "Задачи о моей Родине - Кузбассе" - скачать бесплатно
Презентация по математике "Задачи о моей Родине - Кузбассе" - скачать бесплатно Правильная четырехугольная пирамида. Задачи
Правильная четырехугольная пирамида. Задачи Лесная школа. Умножение и деление. Задачи в стихах
Лесная школа. Умножение и деление. Задачи в стихах Решение задач на основные теоремы теории вероятностей и на формулу полной вероятности
Решение задач на основные теоремы теории вероятностей и на формулу полной вероятности Решение задач на проценты
Решение задач на проценты Занимательные задачи по математике Выполнили: Баринова Катя Крылова Света Галкина Лера 7А класс
Занимательные задачи по математике Выполнили: Баринова Катя Крылова Света Галкина Лера 7А класс Простые и сложные проценты. Составитель: учитель математики МОУ Кулуевская СОШ Ишбирдина Таслима Нуховна
Простые и сложные проценты. Составитель: учитель математики МОУ Кулуевская СОШ Ишбирдина Таслима Нуховна Базовые логические операции и функции. Таблицы истинности. Контактные схемы
Базовые логические операции и функции. Таблицы истинности. Контактные схемы История возникновения и развития геометрии
История возникновения и развития геометрии Системы линейных уравнений с двумя переменными. 7 класс
Системы линейных уравнений с двумя переменными. 7 класс Конус. Площадь поверхности конуса. Развертка конуса
Конус. Площадь поверхности конуса. Развертка конуса Школа волшебников
Школа волшебников Тест по теме «Проценты»
Тест по теме «Проценты» Презентация на тему Дробные числительные
Презентация на тему Дробные числительные  Презентация по математике "Координаты" - скачать бесплатно
Презентация по математике "Координаты" - скачать бесплатно Модель парной линейной регрессии
Модель парной линейной регрессии Презентация на тему МАТЕМАТИЧЕСКИЙ ВЕЧЕР ДЛЯ СТАРШЕКЛАССНИКОВ
Презентация на тему МАТЕМАТИЧЕСКИЙ ВЕЧЕР ДЛЯ СТАРШЕКЛАССНИКОВ  Логическая математика. Занятие математического кружка в 4 классе
Логическая математика. Занятие математического кружка в 4 классе Метод математической индукции
Метод математической индукции Разложение многочлена на множители
Разложение многочлена на множители Деление дробей. 6 класс
Деление дробей. 6 класс Прямоугольный треугольник
Прямоугольный треугольник Теорема Пифагора. Египетский треугольник
Теорема Пифагора. Египетский треугольник Геометрический рисунок. Радиус, центр шара (сферы), диаметр. 6 класс
Геометрический рисунок. Радиус, центр шара (сферы), диаметр. 6 класс