Forecasting with bayesian techniques MP

Lecture Objectives

Introduce the idea of and rationale for Bayesian perspective

Introduction: Two Perspectives in Econometrics

Let θ be a vector of parameters

Outline

Why a Bayesian Approach to VARs?
Brief Introduction to Bayesian Econometrics
Analytical Examples
Estimating

Why a Bayesian Approach to VAR?

Dimensionality problem with VARs:
y contains

Usually, only a fraction of estimated coefficients are statistically significant
parsimonious modeling

Combining information: prior and posterior

Bayesian coefficient estimates combine information in the

Shrinkage

There are many approaches to reducing over-parameterization in VARs
A common idea

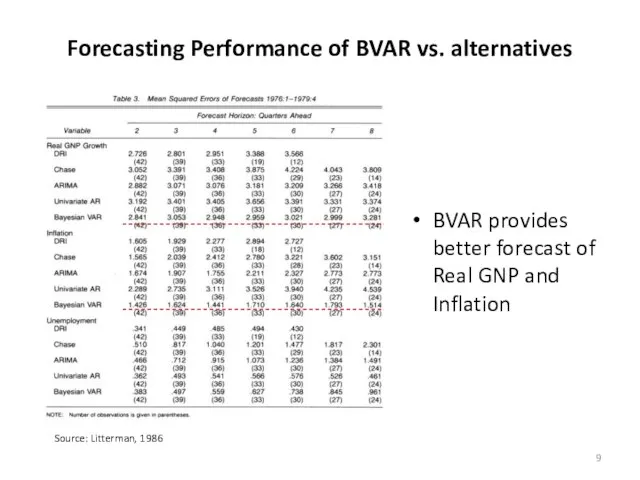
Forecasting Performance of BVAR vs. alternatives

Source: Litterman, 1986

BVAR provides better forecast

Introduction to Bayesian Econometrics: Objects of Interest

Objects of interest:
Prior distribution:
Likelihood function:

Bayesian Econometrics: Objects of Interest (2)

The marginal likelihood…
…is independent of

Bayesian Econometrics: maximizing criterion

For practical purposes, it is useful to focus

Bayesian Econometrics : maximizing criterion (2)

Maximizing C(θ) gives the Bayes mode.

Analytical Examples

Let’s work on some analytical examples:
Sample mean
Linear regression model

Estimating a Sample Mean

Let yt～ i.i.d. N(μ,σ2), then the data density

Estimating a Sample Mean

The posterior of μ:
…has the following analytical form

Estimating a Sample Mean: Example

Assume the true distribution is Normal yt~N(3,1)
So,

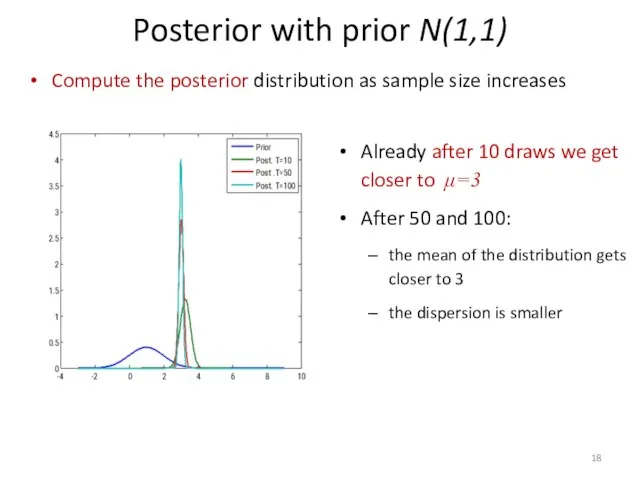
Compute the posterior distribution as sample size increases

Posterior with prior N(1,1)

Already

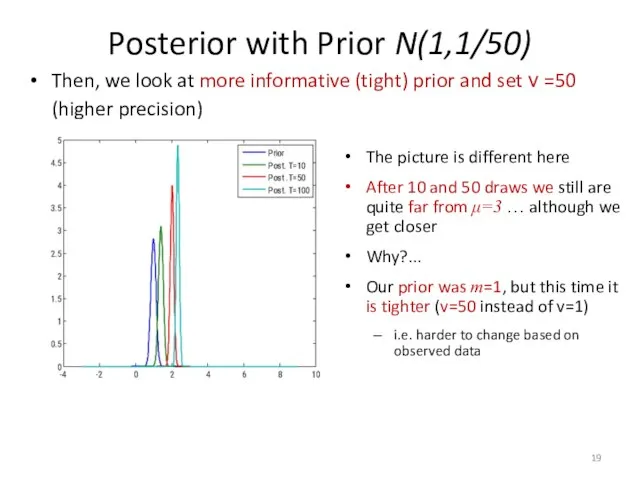
Then, we look at more informative (tight) prior and set ν

Examples: Regression Model I

Linear Regression model:
where ut～ i.i.d. N(0,σ2)
Assume:
β is

Assume that the prior mean of β has multivariate Normal distribution

Examples: Regression Model I (3)

We mix information – densities of data

Since we do not like black boxes… there are 2 ways

Define a “new” regression model
We simply stack our “ingredients” together to

Examples: Regression Model II

So far the life was easy(-ier), in the

Examples: Regression Model II ()

To manipulate the product
…we assume the

Examples: Regression Model II (3)

By manipulating the product (see more details

Priors: summary

In the above examples we dealt with 2 types

Bayesian VARs

Linear Regression examples will help us to deal with our

VAR in a matrix form: example

Consider, as an example, a VAR

How to Estimate a BVAR: Case 1 Prior

Consider Case 1 prior

Before we see the case of an unknown Σe
need to introduce

How to Estimate a BVAR: Conjugate Priors

Assume Conjugate priors:
The VAR parameters

BVARs: Minnesota Prior Implementation

The Minnesota prior – a particular case of

The Minnesota prior
The prior variance for the coefficient of lag k

The Minnesota prior
Interpretation:
the prior on the first own lag is

BVARs: Minnesota Prior Implementation

BVARs: Prior Selection

Minnesota and conjugate priors are useful (e.g., to obtain

Del Negro and Schorfheide (2004): DSGE-VAR Approach

Del Negro and Schorfheide (2004)
We

Del Negro and Schorfheide (2004)

We estimate the following BVAR:
The solution for

Del Negro and Schorfheide (2004)

Parameter λ is a “weight” of “artificial”

Likelihood of the VAR of a DSGE Model

Recall the likelihood function

Next step: we simulate s→∞ artificial observations (Y*,X*) from the DSGE
…and

Conditional on the parameters θ, the DSGE m+odel provides a conjugate

DSGE-VAR posterior

Posterior, conditional on θ :
where

Prior info, weighted by λT

Information from

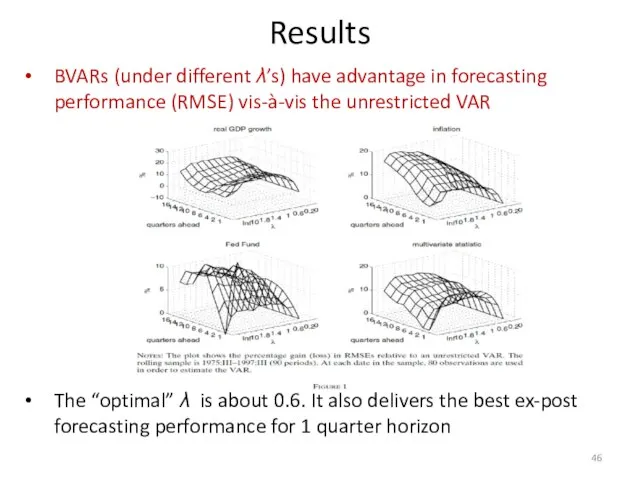
BVARs (under different λ’s) have advantage in forecasting performance (RMSE) vis-à-vis

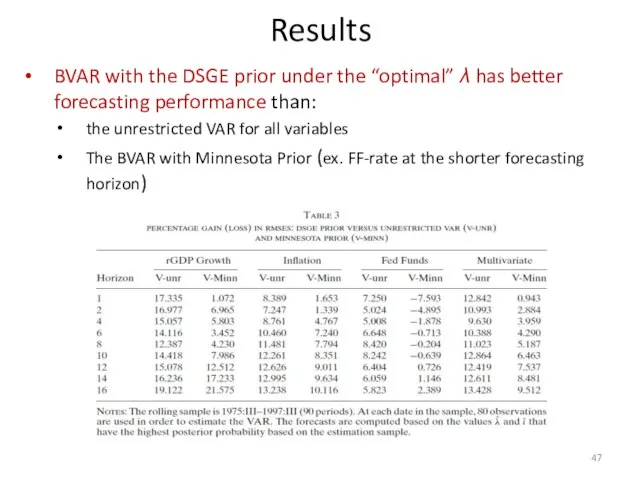
BVAR with the DSGE prior under the “optimal” λ has better

Kadiyala and Karlsson (1997)

Small Model: a bivariate VAR with unemployment and

Kadiyala and Karlsson (1997)

Compare different priors based on the VAR forecasting

Prior distributions in K&K

K&K use a number of competing prior distributions…

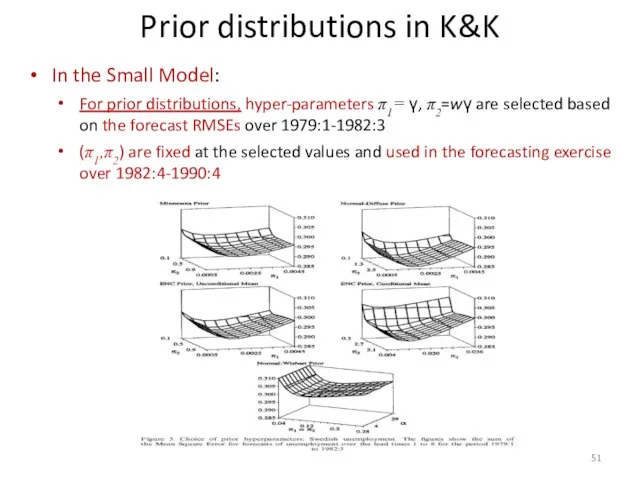
Prior distributions in K&K

In the Small Model:
For prior distributions, hyper-parameters π1=

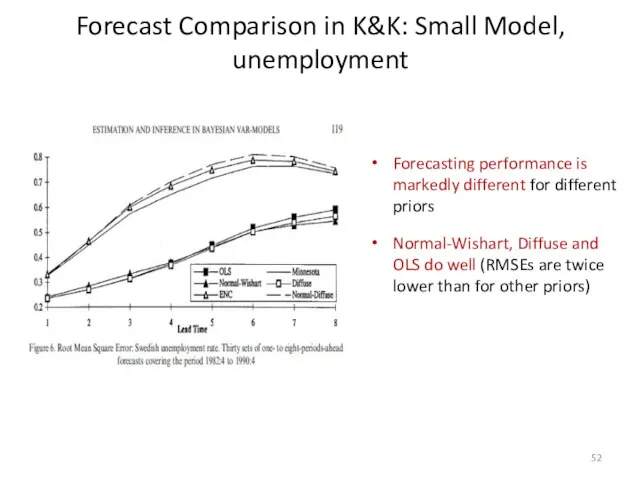
Forecast Comparison in K&K: Small Model, unemployment

Forecasting performance is markedly

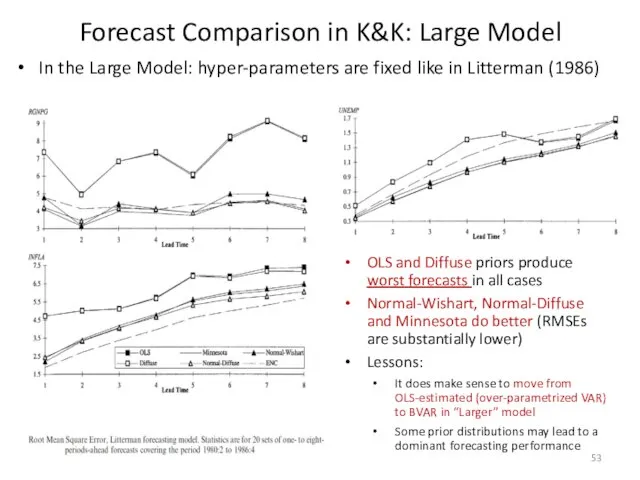
Forecast Comparison in K&K: Large Model

OLS and Diffuse priors produce worst

Giannone, Lenza and Primiceri (2011)

Use three VARs to compare forecasting performance
Small

Giannone, Lenza and Primiceri (2011)

The marginal likelihood is obtained by integrating

Giannone, Lenza and Primiceri (2011)

We interpret the model as a hierarchical

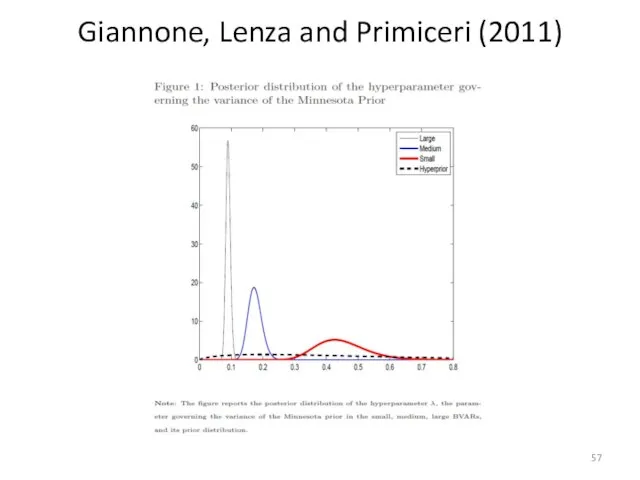
Giannone, Lenza and Primiceri (2011)

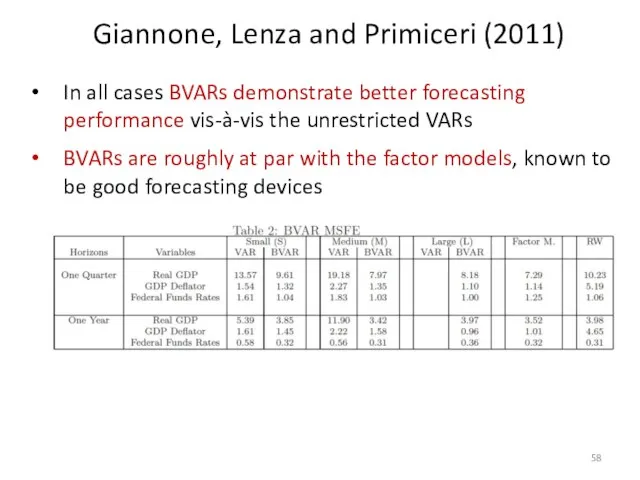
In all cases BVARs demonstrate better forecasting performance vis-à-vis the unrestricted

Conclusions

BVARs is a useful tool to improve forecasts
This is not a

Thank You!

Appendix A: Remarks about the marginal likelihood

Remarks about the marginal likelihood:
If

Appendix A: Remarks about the marginal likelihood

Remarks about the marginal likelihood:
Predict

Appendix B: Linear Regression with conjugate priors

To calculate the posterior distribution

Rearranging the expressions under the exponents we have the following:
where

Therefore we have Normal posterior distribution for β:
β|σ2 ̴ N(m*,

Appendix C: How to Estimate a BVAR, Case 1 prior

Use GLS

Appendix C: How to Estimate a BVAR, Case 1 Prior

Continue
So, the

Appendix D: How to Estimate a BVAR: Conjugate Priors

Note that in

Appendix E: Prior and Posterior distributions in Kadiyala and Karlsson (1997)

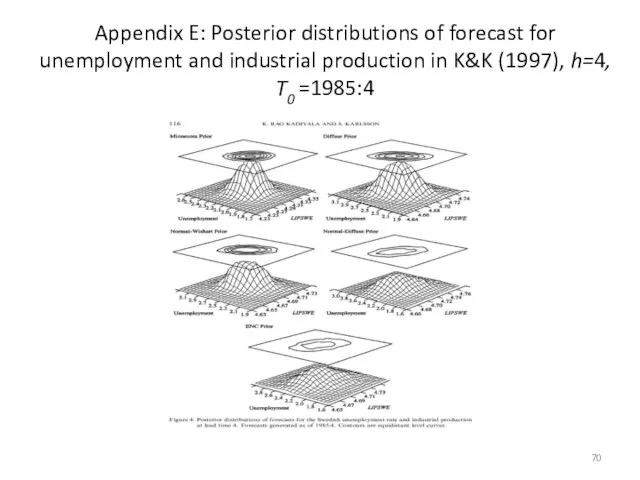
Appendix E: Posterior distributions of forecast for unemployment and industrial production

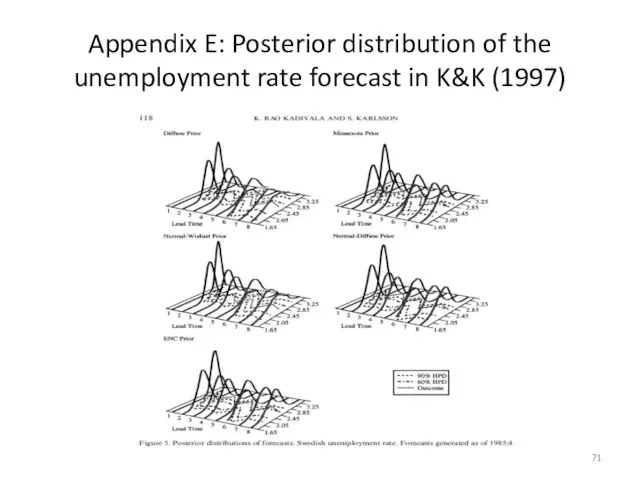
Appendix E: Posterior distribution of the unemployment rate forecast in K&K