Содержание
- 2. 2. Вектор-строка - матрица размера 1×n: A=(a1 a2…an) 1. Вектор-столбец - матрица размера m×1: В квадратной
- 3. 3. Матрица, у которой все элементы aij=0, называется нулевой матрицей (обозначение 0). 5. Квадратная матрица называется
- 4. Операции над матрицами 1. Сравнение Две матрицы А и В одинаковой размерности равны, если у них
- 5. Пример: Пусть Тогда Свойства: А + В = В + А (А + В) + С
- 6. 3. Умножение матрицы на действительное число Произведением матрицы А(mxn) на число λ∈R называется матрица той же
- 7. 4. Умножение вектора-строки на вектор-столбец Произведением вектора-строки А(1×n) на вектор-столбец В(n×1) называется число, равное сумме произведений
- 8. Пусть Произведением матрицы А (m×n) на матрицу В (n×k) называется матрица С (m×k) , элементы сij
- 9. Свойства: А · В ≠ В · А А · (В + С) = А ·
- 10. Пример: Найти произведение матриц Степень Аn = A · A · … · A Свойства: А0
- 12. Скачать презентацию



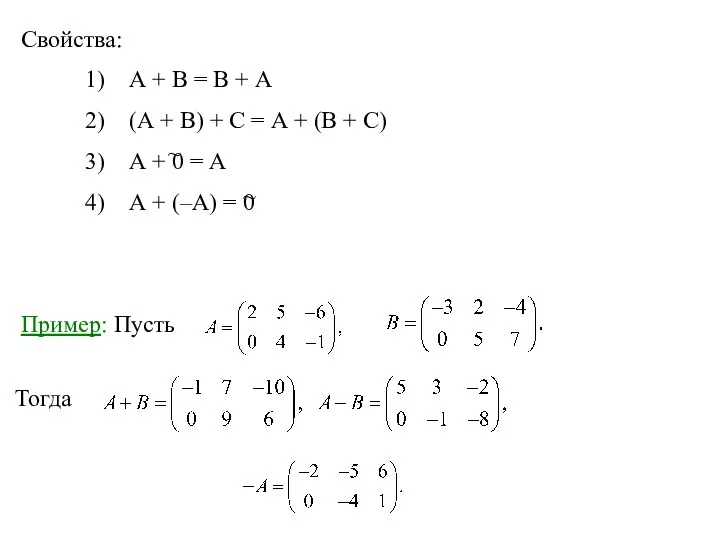





 Функции нескольких переменных. Частные производные
Функции нескольких переменных. Частные производные Окружность и длина окружности
Окружность и длина окружности Функция. Область определения. 9 класс
Функция. Область определения. 9 класс Нумерация чисел. Счет предметов. Разряды
Нумерация чисел. Счет предметов. Разряды Измерение углов
Измерение углов Симметрия. 11 класс
Симметрия. 11 класс Проценты. 6 класс
Проценты. 6 класс Построение и преобразование графиков квадратичной функции. Графические возможности Excel
Построение и преобразование графиков квадратичной функции. Графические возможности Excel Ряды Фурье для четных и нечетных функций
Ряды Фурье для четных и нечетных функций Возможности динамических (электронных) таблиц. Математическая обработка числовых данных. Часть 2
Возможности динамических (электронных) таблиц. Математическая обработка числовых данных. Часть 2 Дифференциальным уравнением
Дифференциальным уравнением Длина окружности и площадь круга
Длина окружности и площадь круга Аналіз алгоритмів
Аналіз алгоритмів Четырехугольники
Четырехугольники  Презентация по математике "Решение задач на разностное и кратное сравнение чисел" - скачать бесплатно
Презентация по математике "Решение задач на разностное и кратное сравнение чисел" - скачать бесплатно Уравнения и неравенства. 11 класс
Уравнения и неравенства. 11 класс Графики функций
Графики функций История возникновения и развития математики
История возникновения и развития математики Математика вокруг нас
Математика вокруг нас Производные высших порядков
Производные высших порядков Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Презентация на тему Единицы площади Обобщение
Презентация на тему Единицы площади Обобщение  Производная и первообразная. Применение производной к исследованию функций
Производная и первообразная. Применение производной к исследованию функций Одночлен презентация_
Одночлен презентация_ Уравнение Эйлера
Уравнение Эйлера Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Геометрический смысл производной
Геометрический смысл производной Параметры полета ракеты
Параметры полета ракеты