Содержание
- 2. Человек сначала научился пользоваться натуральными числами, затем появились рациональные дроби, затем ноль и отрицательные числа и
- 3. ОСНОВНЫЕ ЗАКОНЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ коммутативный закон сложения m + n = n + m .
- 4. РАСШИРЕНИЕ ПОНЯТИЯ ЧИСЛА На множестве натуральных чисел мы всегда можем производить действия сложения и умножения, но
- 5. ЧИСЛОВЫЕ МНОЖЕСТВА: N – бесконечное упорядоченное, дискретное с начальным элементом и без конечного элемента. Замкнутое относительно
- 6. ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА Множество, на котором заданы операции сложения и умножения, удовлетворяющие основным законам 1-5, и
- 7. ОПРЕДЕЛЕНИЕ Ко́мпле́ксные чи́сла (устар. мнимые числа) — числа вида {x+iy}, где {x} и { y} —
- 8. КОМПЛЕКСНЫЕ ЧИСЛА Для нового множества чисел справедливы основные законы 1-5. При этом для комплексных чисел определено
- 9. Результаты арифметических операций с комплексными числами совпадают с результатами, которые мы получили бы, действуя с вещественными
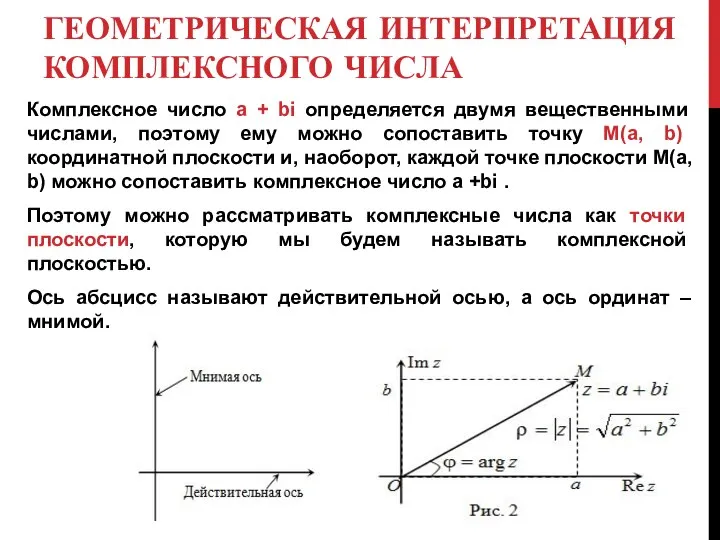
- 10. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНОГО ЧИСЛА Комплексное число a + bi определяется двумя вещественными числами, поэтому ему можно
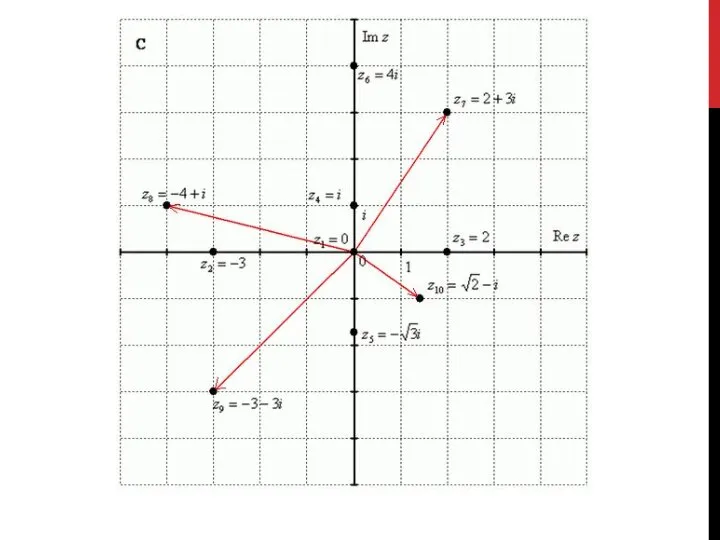
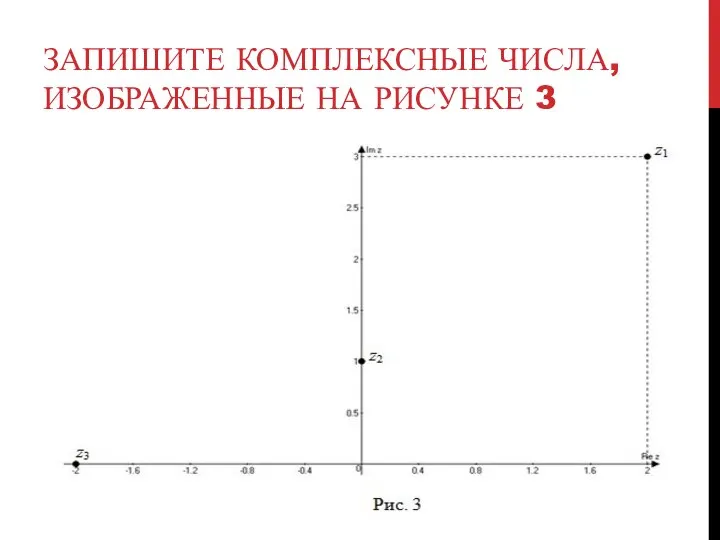
- 12. ЗАПИШИТЕ КОМПЛЕКСНЫЕ ЧИСЛА, ИЗОБРАЖЕННЫЕ НА РИСУНКЕ 3
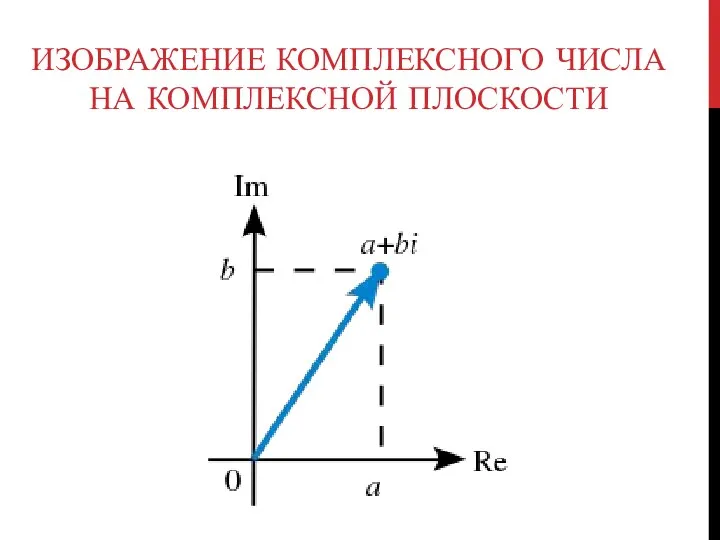
- 13. ИЗОБРАЖЕНИЕ КОМПЛЕКСНОГО ЧИСЛА НА КОМПЛЕКСНОЙ ПЛОСКОСТИ
- 14. КОМПЛЕКСНО-СОПРЯЖЕННЫЕ ЧИСЛА
- 15. СВОЙСТВА КОМПЛЕКСНО СОПРЯЖЕННЫХ ЧИСЕЛ
- 20. АЛГЕБРАИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
- 22. ОПЕРАЦИИ С КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
- 23. СЛОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
- 24. ВЫЧИТАНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
- 25. УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
- 26. ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
- 27. ВОЗВЕДЕНИЕ В СТЕПЕНЬ
- 28. ИЗВЛЕЧЕНИЕ КОРНЕЙ ИЗ КОМПЛЕКСНЫХ ЧИСЕЛ
- 29. ИЗВЛЕЧЕНИЕ КОРНЯ ИЗ КОМПЛЕКСНОГО ЧИСЛА
- 30. РЕШИТЬ КВАДРАТНОЕ УРАВНЕНИЕ
- 31. РЕШИТЬ Найти корни уравнения и разложить квадратный двучлен на множители.
- 33. Скачать презентацию


























 Прямоугольный параллелепипед. Задача на сечение
Прямоугольный параллелепипед. Задача на сечение Деловая игра «Дизайнеры». Занятие на тему: «Паркеты из правильных многоугольников»
Деловая игра «Дизайнеры». Занятие на тему: «Паркеты из правильных многоугольников» Основы теории фракталов
Основы теории фракталов Презентация по математике "«Десятичные дроби» 6 класс" - скачать бесплатно
Презентация по математике "«Десятичные дроби» 6 класс" - скачать бесплатно Диаметр окружности
Диаметр окружности Решение уравнений (2 класс)
Решение уравнений (2 класс) Математический диктант по теме: Сечения конуса и цилиндра
Математический диктант по теме: Сечения конуса и цилиндра Решение простейших тригонометрических неравенств (10 класс)
Решение простейших тригонометрических неравенств (10 класс) Длина окружности и площадь круга. Решение задач. 9 класс
Длина окружности и площадь круга. Решение задач. 9 класс Отношение двух чисел. Работа с математической моделью
Отношение двух чисел. Работа с математической моделью Игра "Экология и математика"
Игра "Экология и математика" Презентация по математике "Стань отличником по математике" - скачать бесплатно
Презентация по математике "Стань отличником по математике" - скачать бесплатно Похідна функції, її геометричний та фізичний зміст
Похідна функції, її геометричний та фізичний зміст Презентация Прямоугольный параллелепипед
Презентация Прямоугольный параллелепипед  Асимптоты графика функции
Асимптоты графика функции Симметрия относительно точки
Симметрия относительно точки Показательные неравенства
Показательные неравенства Презентация по математике "Единицы площади урок" - скачать
Презентация по математике "Единицы площади урок" - скачать  Аттестационная работа. Образовательная программа внеурочной деятельности по математике в разновозрастной группе
Аттестационная работа. Образовательная программа внеурочной деятельности по математике в разновозрастной группе Логарифмическая функция
Логарифмическая функция Презентация по математике "Приключения мушкетеров. Решение логических задач" - скачать
Презентация по математике "Приключения мушкетеров. Решение логических задач" - скачать  Аттестационная работа. Методическая разработка «Математика и литература - два звена процесса творчества»
Аттестационная работа. Методическая разработка «Математика и литература - два звена процесса творчества» Призма. Дисперсия света в призме
Призма. Дисперсия света в призме Классическое определение вероятности
Классическое определение вероятности Применение компьютерных технологий
Применение компьютерных технологий Формулы сокращенного умножения
Формулы сокращенного умножения Сводка и группировка данных статистического наблюдения
Сводка и группировка данных статистического наблюдения Проценты. Процент от величины
Проценты. Процент от величины