Координатно-параметрический метод решения задач с параметрами

углубленного изучения школьной программы по математике. К тому же задачи с параметрами входят в задания единого государственного экзамена.
Цель работы:
1.Рассмотреть координатно-параметрический метод решения задач с параметрами.
2.Показать его применение при решении различных математических задач.
Для достижения цели были выдвинуты следующие задачи:
Изучить координатно-параметрический метод решения задач с параметром;
Сформировать умения и навыки решения задач с параметрами.

некоторая функция переменной х и числового параметра а.
Отметим два частных случая.

1. Координата х есть функция параметра а:
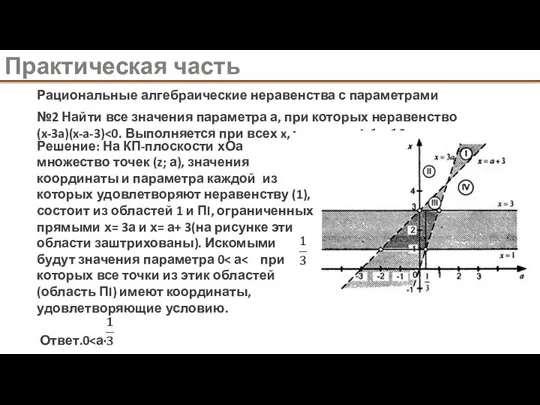
х = f(а), На КП-плоскости хОа с горизонтальной параметрической осью Оа множество всех точек, значения координаты х и параметра а каждой из которых удовлетворяют уравнению (1), представляет собой график функции где роль аргумента функции играет параметр.

2. Параметр а есть функция координаты х:
а = (х)
В этом случае можно рассматривать КП-плоскость аОх с вертикальной параметрической осью Оа и интерпретировать множество всех точек, значения координаты и параметры каждой из которых удовлетворяют уравнению (1), как график функции где роль аргумента функции играет координата.

неравенств с одной переменной при решении неравенств с двумя переменными.

Алгоритм решения:
1) Найти на КП-плоскости ОДЗ (область допустимых значений переменной и параметра) – множество всех точек ,при значениях координаты х и параметра а в каждой из которых выражения P(х,а) определено.
2) Построить на КП - плоскости линии, состоящие из всех точек, при значениях координаты х и параметра а в каждой из которых выражение P(х,а) обращается в нуль или не существует.
3) Разбить этими линиями найденную ОДЗ на «частные области».
4)Исследовать знак выражения P(х,а) в каждой из полученных частных областей. Для этого достаточно установить знак выражении P(х,а)в какой-нибудь точке в каждой из «частных областей».

заменим уравнение совокупностью трех систем.

Рациональные алгебраические уравнения с параметрами

На Координатно-параметрической плоскости решением данного уравнения в первой частичной области (1): х <0 (полуплоскости) является луч во второй области (2): (полосе)-отрезок прямой x=a-1,в третьей области(3): x>1(полуплоскости) - луч . Использую решение на КП-плоскости ,нетрудно записать ответ, поставив в соответствие каждому значению параметра а значение х на полученной ломаной линии.

при всех x, таких, что1 ≤ x ≤ 3

Решение: На КП-плоскости хОа множество точек (z; а), значения координаты и параметра каждой из которых удовлетворяют неравенству (1), состоит из областей 1 и ПI, ограниченных прямыми х= 3а и х= а+ 3(на рисунке эти области заштрихованы). Искомыми будут значения параметра 0< а< при которых все точки из этик областей (область ПI) имеют координаты, удовлетворяющие условию.
Ответ.0<а<

.

Рациональные алгебраические неравенства с параметрами

рационализирующую подстановку, получим
= x + a ⬄ На координатно – параметрической плоскости tOb жирной линией изображено решение смешанной системы.
Исходное уравнение имеет решение при
b = 1 + a ≤ ⬄
Ответ. при a ≤ .

Иррациональные уравнения и неравенства с параметрами

не имеет действительных решений.

Решение. Так как x=1, то данное уравнение можно записать следующим образом:
=0
Полученное тригонометрическое уравнение не имеет действительных решений при всех значениях параметра
На рисунке дана интерпретация решения на КП-плоскости аОх с вертикальной параметрической осью.

Тригонометрические уравнения и неравенства с параметрами

параметрами. Был определен алгоритм, при использовании которого можно решать подобные уравнения. Было наглядно показано, что задачи с параметром можно решать несколькими методами.
При решении приведенных выше задач с параметрами происходит повторение и, как следствие, более глубокое прочное усвоение программных вопросов.