Содержание
- 2. ПРЕДМЕТ: Анализ экспериментальных данных – значений количествен-ного признака (артериальное давление, пульс). Такой признак – случайная величина.
- 3. Часть I. БАЗОВЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- 4. 1. ПОНЯТИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ И ВЫБОРКИ ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ – ВСЕ МНОЖЕСТВО ОБЪЕКТОВ, ОБЛАДАЮЩИХ ДАННЫМ ПРИЗНАКОМ. ВЫБОРКА
- 5. РЕПРЕЗЕНТАТИВНАЯ ВЫБОРКА Чтобы по выборке можно было судить о генеральной совокупности, выборка должна быть РЕПРЕЗЕНТАТИВНОЙ. РЕПРЕЗЕНТАТИВНОЙ
- 6. 2. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ВЫБОРКИ ПРОСТОЙ СТАТИСТИЧЕСКИЙ РЯД РАНЖИРОВАННЫЙ РЯД ВАРИАЦИОННЫЙ РЯД ИНТЕРВАЛЬНЫЙ РЯД ПРОСТОЙ СТАТИСТИЧЕСКИЙ РЯД
- 7. ПОСТРОЕНИЕ РАНЖИРОВАННОГО И ВАРИАЦИОННОГО РЯДОВ РАНЖИРОВАННЫЙ РЯД – ПЕРЕЧИСЛЕНИЕ ЭЛЕМЕНТОВ ВЫБОРКИ В ПОРЯДКЕ ИХ ВОЗРАСТАНИЯ (ИЛИ
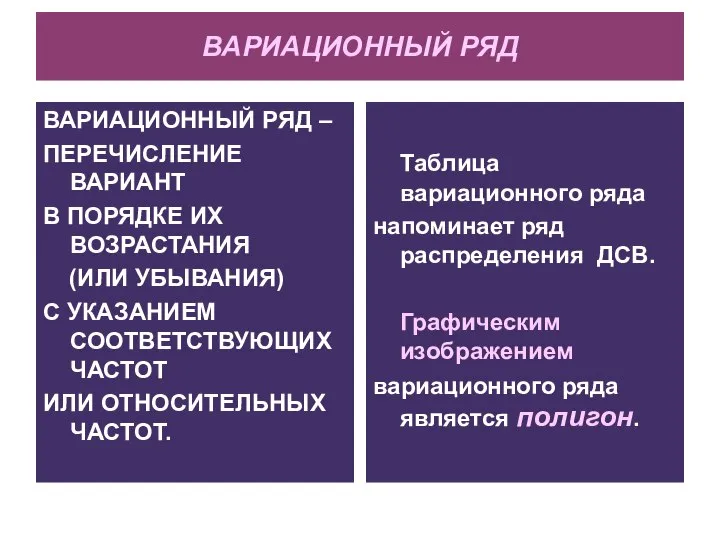
- 8. ВАРИАЦИОННЫЙ РЯД ВАРИАЦИОННЫЙ РЯД – ПЕРЕЧИСЛЕНИЕ ВАРИАНТ В ПОРЯДКЕ ИХ ВОЗРАСТАНИЯ (ИЛИ УБЫВАНИЯ) С УКАЗАНИЕМ СООТВЕТСТВУЮЩИХ
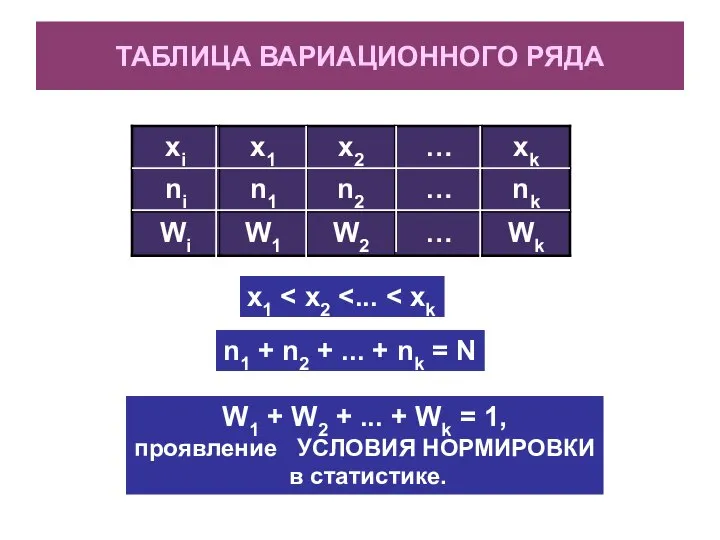
- 9. ТАБЛИЦА ВАРИАЦИОННОГО РЯДА x1 n1 + n2 + ... + nk = N W1 + W2
- 10. ПОЛИГОН ЧАСТОТ или ОТНОСИТЕЛЬНЫХ ЧАСТОТ На оси абсцисс - значения xi , на оси ординат -
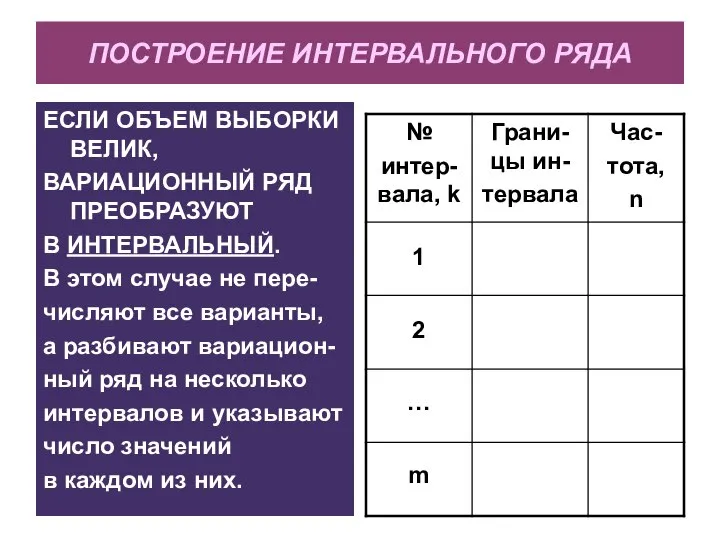
- 11. ПОСТРОЕНИЕ ИНТЕРВАЛЬНОГО РЯДА ЕСЛИ ОБЪЕМ ВЫБОРКИ ВЕЛИК, ВАРИАЦИОННЫЙ РЯД ПРЕОБРАЗУЮТ В ИНТЕРВАЛЬНЫЙ. В этом случае не
- 12. Алгоритм построения интервального ряда Определение разумного числа интервалов: m = log2N, округляем до целого числа. 2.
- 13. 4. Границы интервалов: получаются добавлением шага к предыдущей границе. Граница может входить только в один интер-
- 14. ГИСТОГРАММА Графическое изображение интервального ряда – ГИСТОГРАММА: фигура, состоящая из прямоугольников. Основание каждого прямоугольника - соответствующий
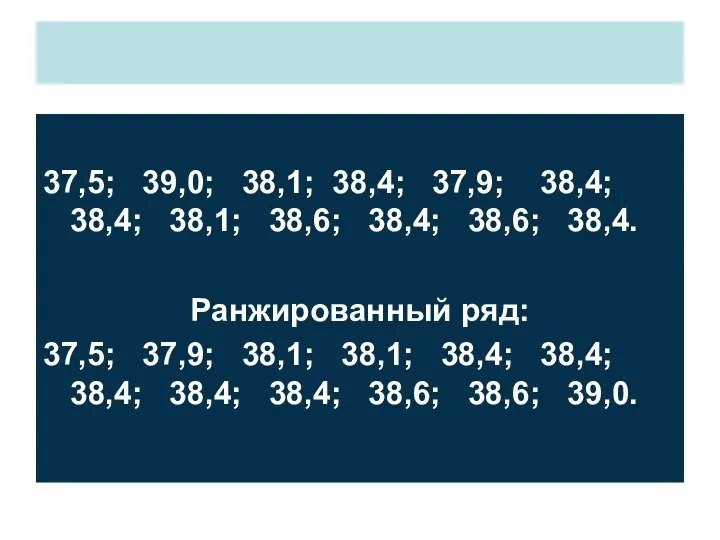
- 15. 37,5; 39,0; 38,1; 38,4; 37,9; 38,4; 38,4; 38,1; 38,6; 38,4; 38,6; 38,4. Ранжированный ряд: 37,5; 37,9;
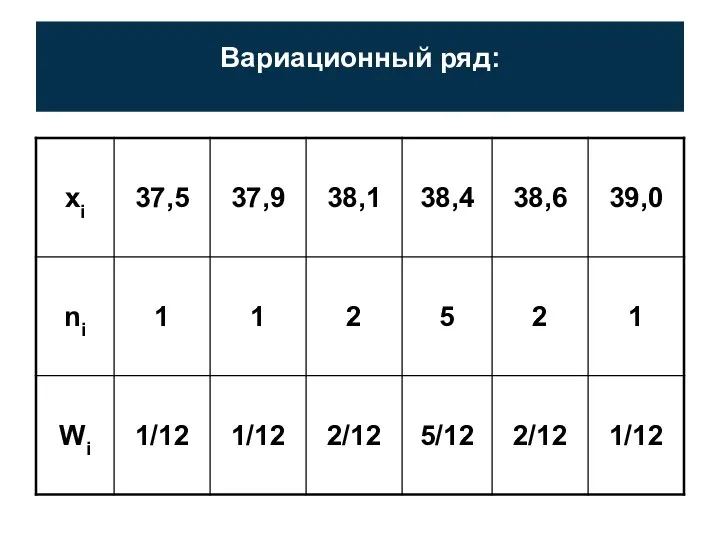
- 16. Вариационный ряд:
- 17. ИНТЕРВАЛЬНЫЙ РЯД: m = log212 ≈ 3; L = 39,0 - 37,5 = 1,5; Δx =
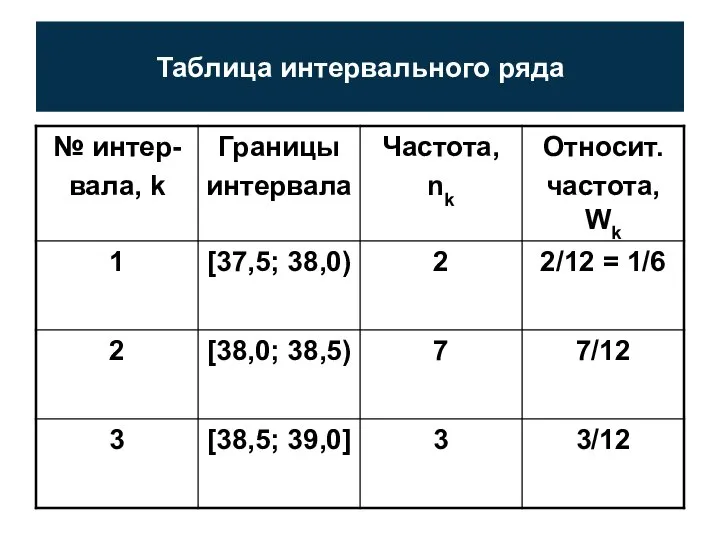
- 18. Таблица интервального ряда
- 19. 3. ХАРАКТЕРИСТИКИ ВЫБОРКИ Средняя выборочная х Выборочная дисперсия Dв = σ2в Выборочное средне-квадратическое отклонение σв Мода
- 20. интервального ряда: Σ сk nk xи = N Здесь сk – середины интервалов: ck = (a
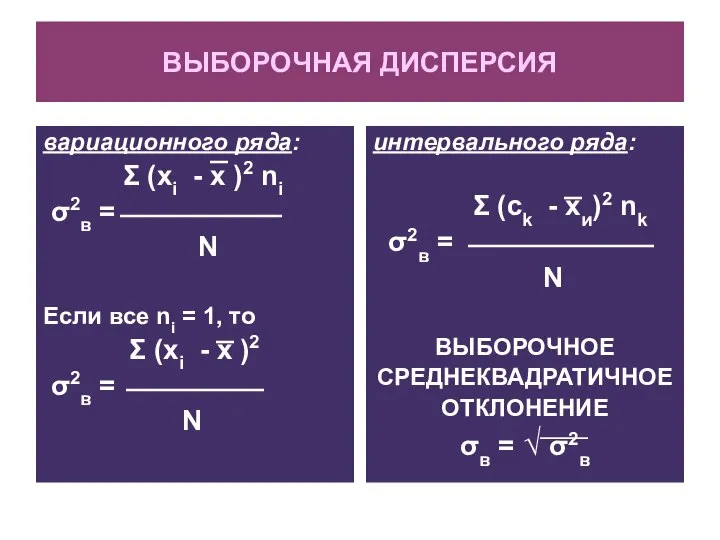
- 21. ВЫБОРОЧНАЯ ДИСПЕРСИЯ вариационного ряда: Σ (xi - x )2 ni σ2в = N Если все ni
- 22. МОДА, МЕДИАНА МОДА – варианта с наибольшей частотой. МЕДИАНА делит вариационный ряд пополам: слева от нее
- 23. 4. ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПО ПАРАМЕТРАМ ВЫБОРКИ ПАРАМЕТРЫ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ – числовые характеристики исследуемой
- 24. Точечные оценки генеральной дисперсии – исправленная дисперсия, s2: σ2 ≈ s2 среднеквадратичного отклонения – стандартное отклонение,
- 25. Таким образом, Σ (xi - x )2 ni s2 = N – 1 Σ (ck -
- 26. 5. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ Дать ИНТЕРВАЛЬНУЮ ОЦЕНКУ того или иного пара- метра генеральной совокупности
- 27. Наряду с доверительной вероятностью используют также понятие УРОВЕНЬ ЗНАЧИМОСТИ β = 1 – γ, т.е. вероятность
- 28. Доверительный интервал для средней теоретической нормально распределенной величины Имеет вид ( х – Δ , х
- 29. Доверительную вероятность задаем сами, обычно в медицине это 95%, то есть γ = 0,95. Точность Δ
- 30. t определяется по надежности с помощью известной формулы теории вероятности: γ = 2Ф (t) – 1.
- 31. Если объем выборки невелик, то вместо таблицы нормального распределения нужно воспользоваться таблицей РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА. Значение t
- 32. Вычислить x и s. По заданной γ рассчитать Ф (t). По значению Ф (t) в таблице
- 34. Скачать презентацию
























 Решение задач, приводящих к умножению дробей
Решение задач, приводящих к умножению дробей Тренажёр-раскраска «Нумерация чисел от 21 до 100»
Тренажёр-раскраска «Нумерация чисел от 21 до 100» Cхема (метод) Горнера. Способ деления многочлена
Cхема (метод) Горнера. Способ деления многочлена Аттестационная работа. Разработка урока «Решение задач на применение второго признака равенства треугольников» 7 класс
Аттестационная работа. Разработка урока «Решение задач на применение второго признака равенства треугольников» 7 класс Числовые промежутки. 8 класс
Числовые промежутки. 8 класс Ошибка измерения. Учет ошибки шкалы прибора и систематических ошибок. Оценка суммарной погрешности
Ошибка измерения. Учет ошибки шкалы прибора и систематических ошибок. Оценка суммарной погрешности Работа с текстовой математической задачей
Работа с текстовой математической задачей Тема: «Положительные и отрицательные числа» 6 класс Урок обобщения и систематизации знаний Презентацию выполнила: Черкасо
Тема: «Положительные и отрицательные числа» 6 класс Урок обобщения и систематизации знаний Презентацию выполнила: Черкасо Комбинаторика. Правило суммы и правило произведения
Комбинаторика. Правило суммы и правило произведения Операції диференціювання. Первісна функція
Операції диференціювання. Первісна функція Решение показательного уравнения
Решение показательного уравнения Порядок выполнения действий
Порядок выполнения действий Делимость чисел
Делимость чисел Сумма углов треугольника ГБОУ СОШ №1358 УЧИТЕЛЬ МАТЕМАТИКИ ЕПИФАНОВА ТАТЬЯНА НИКОЛАЕВНА
Сумма углов треугольника ГБОУ СОШ №1358 УЧИТЕЛЬ МАТЕМАТИКИ ЕПИФАНОВА ТАТЬЯНА НИКОЛАЕВНА  Одночлен и его стандартный вид. 7 класс
Одночлен и его стандартный вид. 7 класс Полезные функции
Полезные функции Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Osnovy_teorii_veroyatnostey
Osnovy_teorii_veroyatnostey Аттестационная работа. Образовательная программа внеурочной деятельности. Создаем проекты по математики. (5 класс)
Аттестационная работа. Образовательная программа внеурочной деятельности. Создаем проекты по математики. (5 класс) Прямоугольный и треугольные обходы
Прямоугольный и треугольные обходы Сложная функция. 10 класс
Сложная функция. 10 класс Непараметрический дисперсионный анализ
Непараметрический дисперсионный анализ Признаки равенства треугольников
Признаки равенства треугольников 11г 12.09
11г 12.09 Построение треугольника
Построение треугольника Взаимно обратные числа. Урок № 1. 6 класс
Взаимно обратные числа. Урок № 1. 6 класс Математические ребусы
Математические ребусы Логическая модель. Логика высказываний. Основы логики высказываний
Логическая модель. Логика высказываний. Основы логики высказываний