Линейная алгебра

Структура курса

-линейная алгебра;
-векторная алгебра;
-аналитическая геометрия.

Литература

Математика. Ч. 1, 1 семестр: УМК /сост.: А.Б.Гончарова и др.– СПб.:

Матрицы

ЛЕКЦИЯ 1

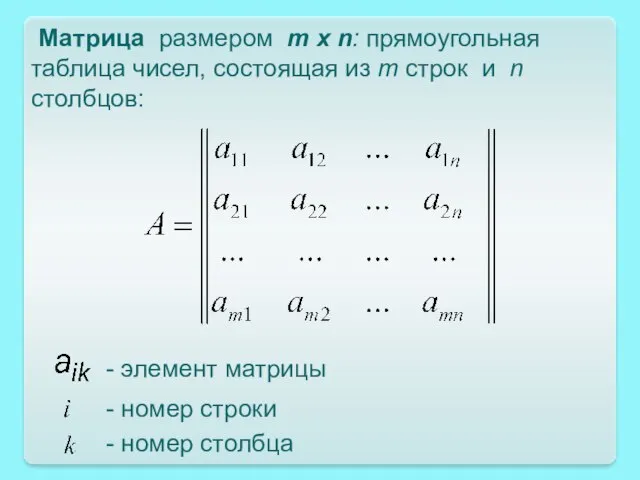
Матрица размером m x n: прямоугольная таблица чисел, состоящая из

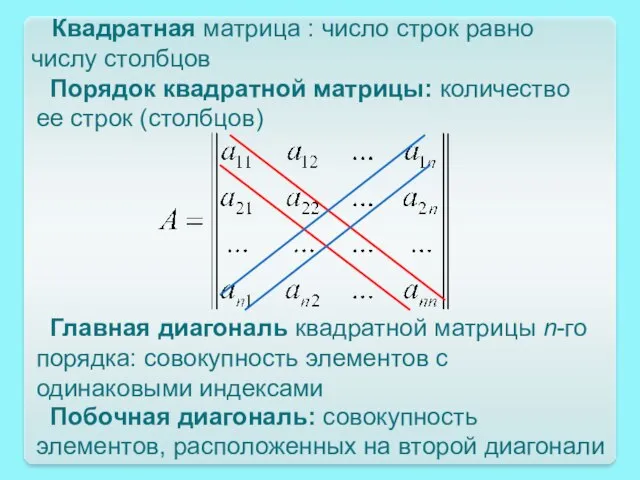
Главная диагональ квадратной матрицы n-го порядка: совокупность элементов с одинаковыми

Диагональная матрица: квадратная матрица, все элементы которой, расположенные вне главной диагонали,

Равные матрицы A и B: имеют одинаковый размер и их

Транспонированная матрица: столбцы матрицы А являются строками матрицы

Разность матриц A

Пример.

Произведение матрицы A (m x p) на матрицу B(p x n)

Пример. Вычислить произведение матрицы А на матрицу В справа:

Пример. Вычислить произведение матрицы А на матрицу В слева.

Пример. Доказать, что матрицы А и В перестановочные

Определитель матрицы второго порядка:

Определители квадратных матриц

число, равное разности произведений

Пример. Вычислить определитель матрицы

Минор элемента матрицы третьего порядка: определитель матрицы второго порядка, получающейся из

Пример.

Определитель матрицы третьего порядка: число, равное сумме произведений элементов любой

Пример. Вычислить определитель матрицы разложением по первой строке

Пример. Вычислить определитель матрицы разложением по второму столбцу

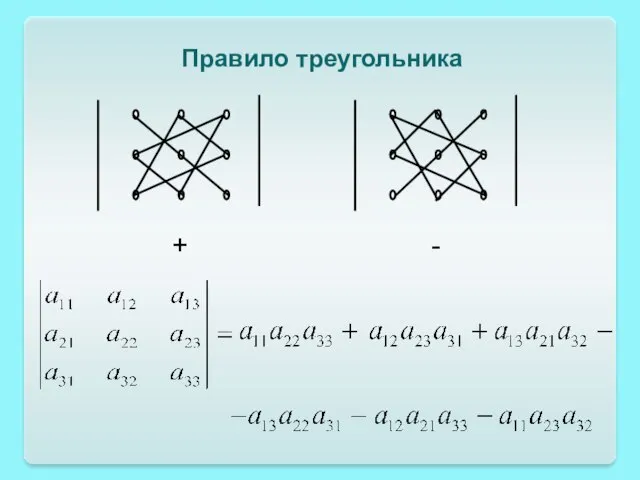
Правило треугольника

+

-

Пример. Вычислить определитель матрицы по правилу треугольника

Пример . Вычислить определитель, разложив
его по элементам первого столбца

Пример . Вычислить определитель, используя
правило треугольника

Основные свойства определителей

1.Определитель транспонированной матрицы равен определителю исходной матрицы

2. Сумма

5. Умножение определителя на число эквивалентно умножению строки (столбца) на

*2+

0

Пример. Вычислить определитель

*2+

*(-3)+

*(-5)+

Пример.

Квадратная матрица А называется обратимой, если существует обратная к ней матрица

Свойства обратных матриц

Пример. Найти обратную матрицу для матрицы

Проверка:

Самостоятельная работа №1

1. Алгебраическое дополнение элемента
матрицы равно...

1) 2

2) -2

3)

Самостоятельная работа №1

3. Определитель равен .....

1) -1

2) -5

3) 5

4) 1

4.

Самостоятельная работа №1

5. Сумма элементов побочной диагонали матрицы произведения матрицы

Самостоятельная работа №1

1. Если определитель матрицы
равен D, то определитель
матрицы равен…..

Самостоятельная работа №1

3. Матрица является обратной
по отношению к матрице при k=…

4