Содержание
- 2. Ричард Олдингтон (1892 – 1962гг..) - английский поэт, прозаик, критик «Ничему тому, что важно знать, научить
- 3. Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением. Решение логарифмических
- 4. Ответ: 4. Пример 3: Ответ: Пример 2: В таких уравнениях нет посторонних корней, поэтому проверка не
- 5. Способы решения логарифмических уравнений Решение уравнений на основании определения логарифма, например, уравнение loga х = б
- 6. 2. Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их.
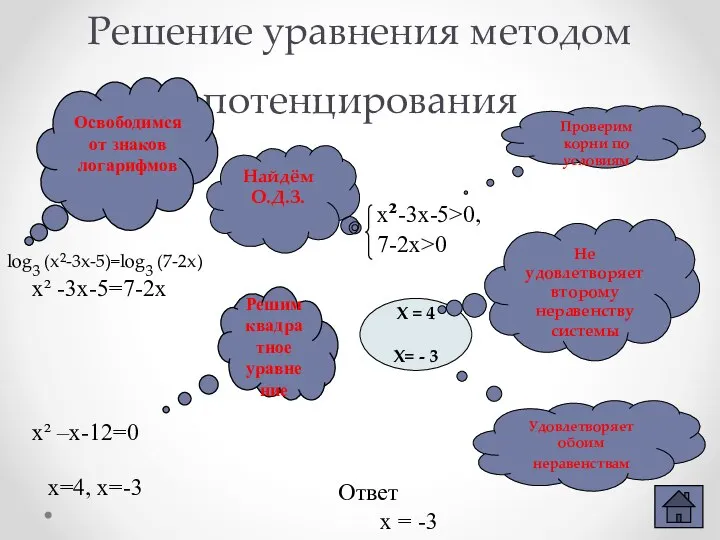
- 7. Метод потенцирования (с нахождением ОДЗ) log3 (x²-3x-5)=log3 (7-2x) Записать условия, определяющие область допустимых значений (О.Д.З.): f
- 8. Решение уравнения методом потенцирования log3 (x²-3x-5)=log3 (7-2x) х² -3х-5=7-2х х² –х-12=0 Решим квадратное уравнение х=4, х=-3
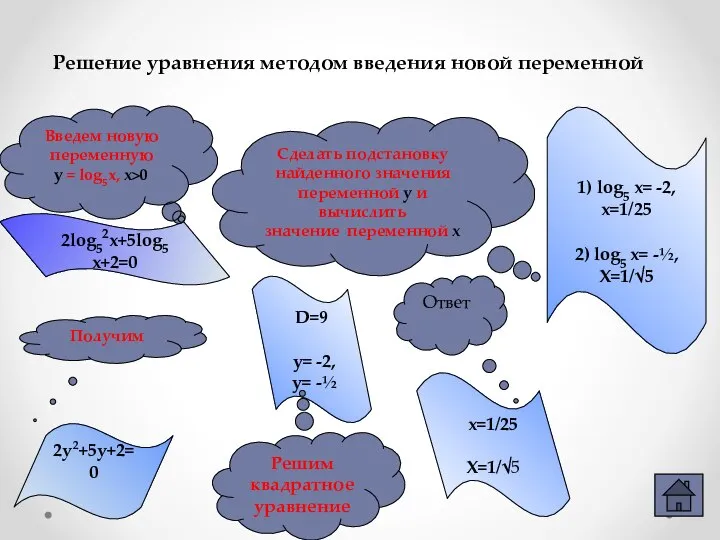
- 9. 3.Метод введения новой переменной(алгоритм) 2log25x+5log5x+2=0 Ввести новую переменную, найти О.Д.З. Решить получившееся уравнение и найти значение
- 10. Решение уравнения методом введения новой переменной 2log52x+5log5 x+2=0 Получим D=9 y= -2, y= -½ 1) log5
- 11. Введение новой переменной. Решить уравнение: Решение: ОДЗ: х > 0. Пусть , тогда уравнение примет вид:
- 12. Пример Ответ: ОДЗ: Пусть тогда Значит, или
- 13. 4. Метод логарифмирования обеих частей уравнения. Если в показатели степени содержится логарифм, то обе части уравнения
- 14. 4метод: Решите уравнение = ЗХ , возьмем от обеих частей уравнения логарифм по основанию 3 Вопрос
- 15. Метод логарифмирования. Пример : Ответ: 3; 27. ОДЗ: Пусть тогда Значит, или
- 16. 5. Метод приведения логарифмов к одному и тому основанию.
- 17. Решение уравнений с разными основаниями Опираясь на свойство:
- 18. Пример : Ответ: ОДЗ: Приведём логарифмы к одному основанию – 7: Подстановка: Уравнение примет вид: Значит,
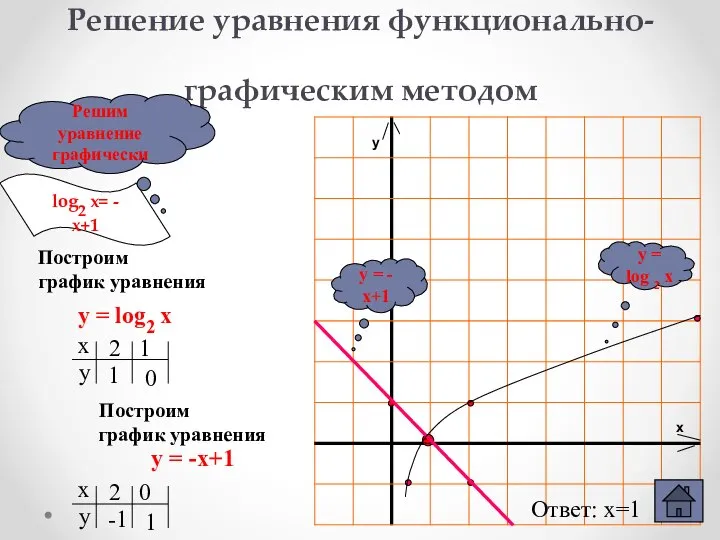
- 19. Функционально-графический метод(алгоритм) log2x = -x+1 Ввести функцию f(x),равную левой части и g(x),равную правой части Построить на
- 20. Решение уравнения функционально-графическим методом Построим график уравнения у = -х+1 у = log2 x Построим график
- 21. Решите самостоятельно:
- 23. Скачать презентацию
















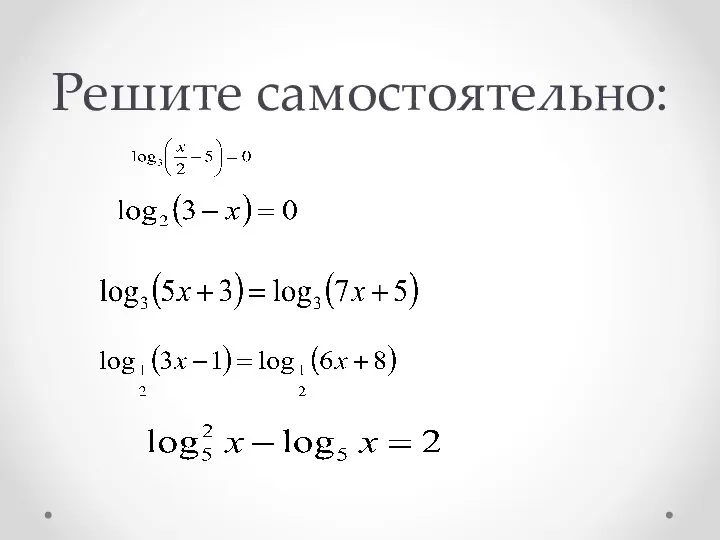
 Решение задач. Касательная к окружности
Решение задач. Касательная к окружности Свойства параллельных плоскостей
Свойства параллельных плоскостей Аттестационная работа. Программа внеурочной деятельности по математике В мире чисел и задач. (7 класс)
Аттестационная работа. Программа внеурочной деятельности по математике В мире чисел и задач. (7 класс) Возникновение геометрии
Возникновение геометрии Тренажер «Считаем с Колобком»
Тренажер «Считаем с Колобком» Геометрическая вероятность
Геометрическая вероятность Методы измерения и контроля. Измерительные приборы
Методы измерения и контроля. Измерительные приборы Задачи на нахождение неизвестного уменьшаемого, неизвестного вычитаемого
Задачи на нахождение неизвестного уменьшаемого, неизвестного вычитаемого Задачи на движение
Задачи на движение Числовая окружность
Числовая окружность Аттестационная работа. Методическая разработка программы элективного курса «Тайна чисел». (5 класс)
Аттестационная работа. Методическая разработка программы элективного курса «Тайна чисел». (5 класс) Число и цифра 6 (1 класс)
Число и цифра 6 (1 класс) Временные ряды и их предварительный анализ
Временные ряды и их предварительный анализ Решение дробных рациональных уравнений. Алгебра 8 класс
Решение дробных рациональных уравнений. Алгебра 8 класс Таблица умножения и деления на 3
Таблица умножения и деления на 3 Устойчивость пластин и оболочек
Устойчивость пластин и оболочек Теория вероятностей. Повторение
Теория вероятностей. Повторение Жұмбақ сан
Жұмбақ сан Взаимосвязь математики и архитектуры в симметрии
Взаимосвязь математики и архитектуры в симметрии Параллелепипед. Куб
Параллелепипед. Куб Урок по математике 6 класс « Разложение на простые множители»
Урок по математике 6 класс « Разложение на простые множители»  Частотная таблица
Частотная таблица Решение задач на сложение и умножение вероятностей
Решение задач на сложение и умножение вероятностей Теория игр
Теория игр Деление обыкновенных дробей
Деление обыкновенных дробей Аттестационная работа. Творческий проект «Цифры и числа»
Аттестационная работа. Творческий проект «Цифры и числа» Тест по алгебре и началам анализа
Тест по алгебре и началам анализа Графи. Основні поняття і визначення
Графи. Основні поняття і визначення