Содержание
- 2. План лекции: Введение. Понятие матрицы. Операции с матрицами. Определители, их свойства. Обратная матрица. Характеристическое уравнение матриц.
- 3. Введение Широкое использование математических методов в современном мире требует от будущего психолога умения применять их при
- 4. Введение В современной науке возникли новые направления, такие, например, как математическая лингвистика, математическая биология, математическая экономика
- 5. Введение Объектами исследования математики служат логические модели, построенные для описания процессов, происходящих в обществе, природе, технике,
- 6. Введение Применение математических методов расширяет возможности каждого специалиста. Существенную роль играет раздел математической статистики, которая учит
- 7. Введение Любой психолог, как и математик, должен уметь рассуждать логически, применять на практике дедуктивный и индуктивный
- 8. Матрица это система элементов aij расположенных в виде прямоугольной таблицы. Элементы могут быть числами, функциями или
- 9. Матрица Если матрица имеет m строк и n столбцов, то говорят о (m × n)-матрице. m
- 10. Матрица Первый индекс элемента матрицы указывает номер строки, а второй – номер столбца
- 11. Главной диагональю матрицы называется диагональ, идущая из левого верхнего угла матрицы в правый нижний. При m=n
- 12. Единичная матрица – частный случай диагональной матрицы, в которой все элементы, находящиеся на главной диагонали, равны
- 13. Матрица, все элементы которой равны нулю, называется нулевой матрицей или нуль-матрицей.
- 14. Матрица, состоящая из одной строки, называется строкой (строковой), из одного столбца — столбцом. Если все ai
- 15. Транспонирование матрицы Переставив в матрице строки со столбцами,получают транспонированную матрицу A’, или AT.
- 16. Транспонирование матрицы Например:
- 17. Наряду с конечными матрицами могут быть матрицы с бесконечным числом строк или столбцов
- 18. Действия над матрицами Умножение матрицы на число. Произведением прямоугольной (m × n)-матрицы А на число называют
- 19. Например:
- 20. Сложение матриц Сумма прямоугольных матриц одинакового размера равна: Например:
- 21. Умножение матриц определяется только для прямоугольных матриц таких, что число столбцов первого множителя равно числу строк
- 22. Найти произведение матриц:
- 23. Введённые действия над матрицами обладают свойствами, близкими к свойствам действий над числами. Исключением является отсутствие коммутативного
- 24. Найти произведение матриц: И
- 25. Свойства действия умножения матриц 1.(AB)C = A(BC) - ассоциативность умножения 2.(kA)B = A(kB) = k(AB) 3.
- 26. Определители Пусть дана квадратная матрица второго порядка Определителем второго порядка, соответствующим данной матрице, называется число: a11a22
- 27. Определитель обозначается символом detA, Δ; числа - a11,a12,a21a22 называются элементами определителя; a11,a22 – образуют главную диагональ,
- 28. Свойства определителей Определитель матрицы не меняется, если строки и столбцы меняются местами (транспонирование)
- 29. Свойства определителей Сумма произведений элементов любой строки (любого столбца) на их алгебраические дополнения равна определителю матрицы.
- 30. Свойства определителей Если в определители поменять местами две его любые строки (два любых столбца), то определитель
- 31. Свойства определителей Общий множитель элементов любой строки (столбца) можно выносить за знак определителя. Определитель не изменится,
- 32. Минор Минор Мij элемента аij - определитель полученный в результате вычеркивания i–й строки и j- го
- 33. Пример Дана матрица Матрица миноров имеет вид Находим минор для первого элемента. Оставшееся число и является
- 34. Алгебраическое дополнение Минор Мij умноженный на называется алгебраическим дополнением Аij элемента аij
- 35. Для рассмотренного примера Для второй матрицы необходимо поменять знаки у выделенных членов
- 36. Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:
- 37. Обратная матрица Понятие обратной матрицы вводится только для квадратных матриц. Если A – квадратная матрица, то
- 38. Найти определитель матрицы ІAІ. Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу A′
- 39. Пример: найти обратную матрицу Находим определитель матрицы: ІАІ =1·4 – 2·3 = – 2 Находим матрицу
- 40. Тест Порядок прямоугольной матрицы, имеющей m строк и n столбцов равен 1. (m x n) 2.
- 41. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА: Основная литература: Ганичева А.В., Козлов В.П. Математика для психологов. М.: Аспект-пресс, 2005, с.81-89. Павлушков
- 43. Скачать презентацию

















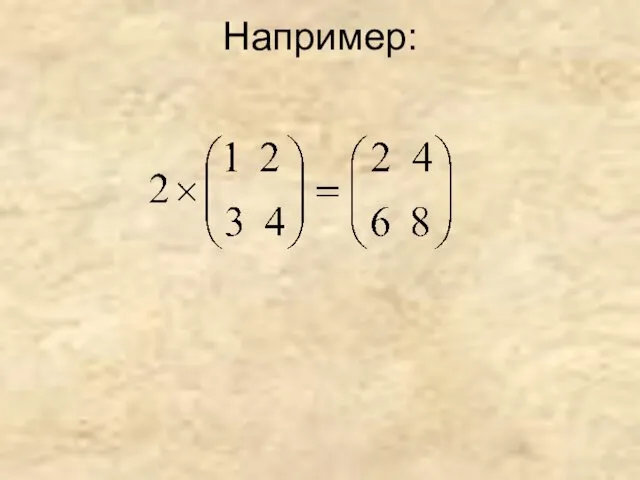






















 Перестановки. Лекция 23
Перестановки. Лекция 23 Степень с целым показателем
Степень с целым показателем Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс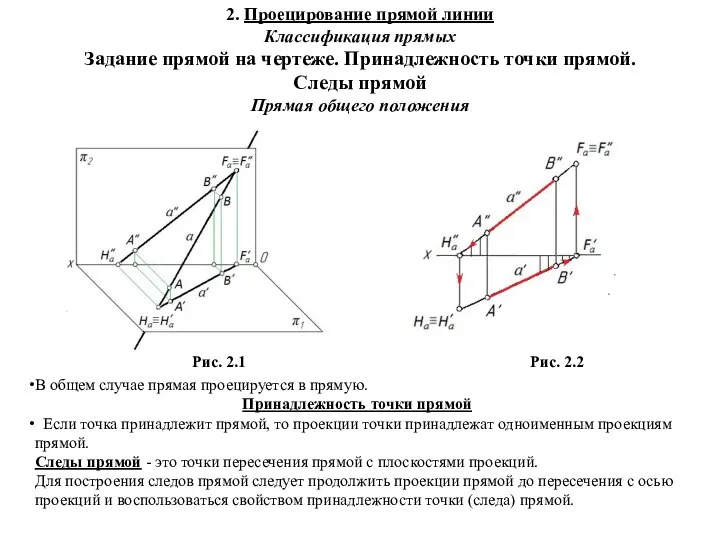 Предмет начертательной геометрии. Проецирование прямой линии. Классификация прямых. Задание прямой на чертеже. (Лекция 2)
Предмет начертательной геометрии. Проецирование прямой линии. Классификация прямых. Задание прямой на чертеже. (Лекция 2) Призмы и антипризмы
Призмы и антипризмы Пересечение поверхностей
Пересечение поверхностей Понятие логарифма
Понятие логарифма Проверка деления с остатком
Проверка деления с остатком Совместные действия с обыкновенными и десятичными дробями
Совместные действия с обыкновенными и десятичными дробями Координатная плоскость. Алгебра 7 класс
Координатная плоскость. Алгебра 7 класс Эталоны и их классификация. (Лекция 3)
Эталоны и их классификация. (Лекция 3) Четвертое измерение
Четвертое измерение Тест по теме: "Векторы в пространстве. Сложение и вычитание векторов. Умножение вектора на число". Вариант 2
Тест по теме: "Векторы в пространстве. Сложение и вычитание векторов. Умножение вектора на число". Вариант 2 Площадь треугольника
Площадь треугольника Метод координат
Метод координат Прямоугольные треугольники
Прямоугольные треугольники Задача двух тел. Уравнения движения в задаче двух тел
Задача двух тел. Уравнения движения в задаче двух тел Виды треугольников. 5 класс
Виды треугольников. 5 класс Пространственные фигуры. Площадь, объем
Пространственные фигуры. Площадь, объем ЛИНЕЙНАЯ ФУНКЦИЯ» Презентация по алгебре для 7 класса
ЛИНЕЙНАЯ ФУНКЦИЯ» Презентация по алгебре для 7 класса  Познайте мир логических задач. Математика и логика неразделимы
Познайте мир логических задач. Математика и логика неразделимы Правила дифференцирования
Правила дифференцирования Числовой отрезок
Числовой отрезок Бирелгән почмакка тигез почмакны циркуль һәм линейка ярдәмендә ничек төзергә
Бирелгән почмакка тигез почмакны циркуль һәм линейка ярдәмендә ничек төзергә Деление десятичных дробей на натуральное число
Деление десятичных дробей на натуральное число Задачи на дроби (3). 6 класс
Задачи на дроби (3). 6 класс Определение и признаки параллелограмма
Определение и признаки параллелограмма Таблица основных неопределенных интегралов
Таблица основных неопределенных интегралов