Содержание
- 2. Далее везде примем обозначение Т.к. определению подлежат две функции то одним соотношением между ними распорядимся произвольно.
- 4. Пример.
- 5. 12.3.7 Линейные дифференциальные уравнения -го порядка. Выше изложенное переносится на дифференциальные уравнения порядка (**) где -
- 6. Линейно независимые системы функций. Рассмотрим систему функций Линейной комбинацией их будет где - постоянные. Определение. Система
- 7. Если не есть линейно независимые функции, то они линейно зависимы. Пример.
- 8. Теорема. Если суть частных линейно независимых решений дифференциального уравнения (***), то общим решением этого уравнения будет
- 9. Условие линейной независимости частных решений дифференциального уравнения Если заданы начальные условия то, чтобы из общего решения
- 10. Линейно независимые решения дифференциального уравнения - го порядка образуют фундаментальную систему решений. Общее решение неоднородного дифференциального
- 11. Теорема. Если - фундаментальная система решений дифференциального уравнения то решением дифференциального уравнения является функция где удовлетворяют
- 12. 12.3.8 Линейные дифференциальные уравнения -го порядка с постоянными коэффициентами и правой частью специального вида. Характеристическое уравнение
- 13. Пример.
- 15. Скачать презентацию

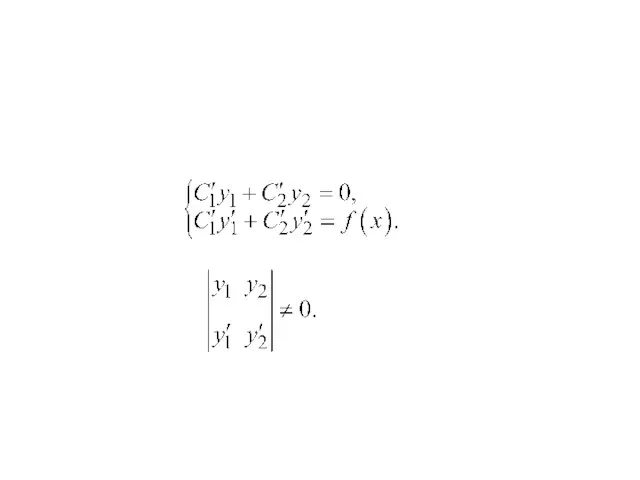










 Сегодня мы будем повторять числительные от 20 до 100
Сегодня мы будем повторять числительные от 20 до 100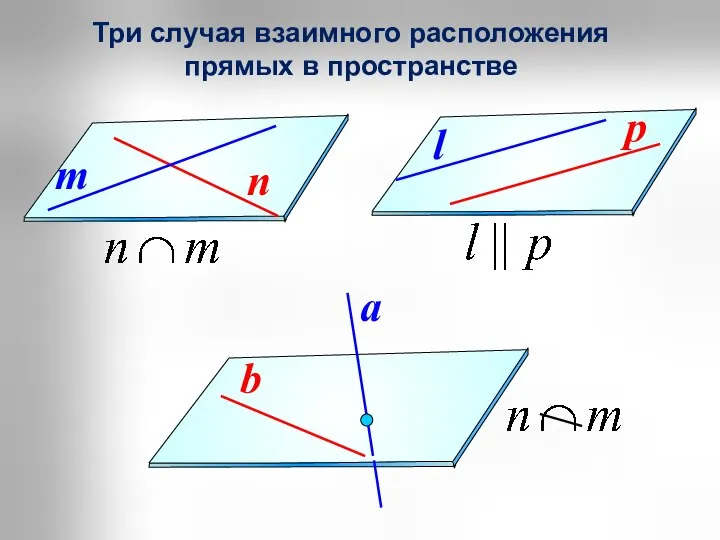 Три случая взаимного расположения прямых в пространстве
Три случая взаимного расположения прямых в пространстве Вычисление объёмов прямой призмы и цилиндра
Вычисление объёмов прямой призмы и цилиндра Свойства преобразования Фурье
Свойства преобразования Фурье Презентация по математике "Натуральные числа" - скачать
Презентация по математике "Натуральные числа" - скачать  Уравнения с разделяющимися переменными. Однородные уравнения. (Семинар 33)
Уравнения с разделяющимися переменными. Однородные уравнения. (Семинар 33) Решение треугольников
Решение треугольников Дробно-рациональные уравнения
Дробно-рациональные уравнения Факториальные кольца
Факториальные кольца Математики России
Математики России Тела вращения. Зачет
Тела вращения. Зачет Числовые функции
Числовые функции Принцип Дирихле. 6 класс
Принцип Дирихле. 6 класс Производная и её применение
Производная и её применение Свойства действий с рациональными числами
Свойства действий с рациональными числами Решение задач на увеличение и уменьшение в несколько раз. 2 класс
Решение задач на увеличение и уменьшение в несколько раз. 2 класс Diagnostika lineárního regresního modelu
Diagnostika lineárního regresního modelu Свойства степени (2)
Свойства степени (2) Экспоненциальные методы для анализа временных рядов
Экспоненциальные методы для анализа временных рядов מדדי פיזור לשילוב
מדדי פיזור לשילוב Необходимость математики в жизни
Необходимость математики в жизни Л. Эйлер и развитие математического анализа в XVIII веке
Л. Эйлер и развитие математического анализа в XVIII веке Нормальные формы для формул алгебры высказываний
Нормальные формы для формул алгебры высказываний § 2.6. Табличное решение логических задач Информатика 7 класс
§ 2.6. Табличное решение логических задач Информатика 7 класс  Обработка результатов измерений
Обработка результатов измерений Куля і сфера. Перерiз сфери площиною
Куля і сфера. Перерiз сфери площиною Цікава математика
Цікава математика Построение графиков тригонометрических функций
Построение графиков тригонометрических функций