Содержание
- 2. Нестандартная задача – это задача, алгоритм решения, которой учащимся неизвестен, то есть учащиеся не знают заранее
- 3. При решении занимательных задач преследуются следующие цели: формирование и развитие мыслительных операций: анализа, синтеза, сравнения, аналогии,
- 4. Нестандартные задачи по математике, используемые в начальной школе, условно можно разделить на следующие группы: задачи на
- 5. Методы решения: алгебраический; арифметический; графический; практический; метод предположения; метод перебора Способы решения: способ рассуждений; способ составления
- 6. На первом этапе учащиеся должны: усвоить процесс решения любой задачи (читаю задачу, выделяю, что известно и
- 7. Памятка Если тебе трудно решить задачу, то попробуй: - сделать к задаче рисунок или чертеж (подумай,
- 8. Задачи на взвешивание – достаточно распространенный вид математических задач. В таких задачах от решающего требуется локализовать
- 9. Задача №1 Из девяти монет одна фальшивая: она легче остальных. Как за два взвешивания на чашечных
- 10. Решение: 2. Одна из кучек легче. Значит в ней фальшивая монета. Разобьём монеты на 3 кучки
- 11. Второе взвешивание: теперь требуется найти фальшивую среди трёх монет ( по методу первого взвешивания).
- 12. Задача №2 В мешке 24 кг гвоздей. Как, имея только чашечные весы без гирь, отмерить 9
- 13. Решение: Основная доступная операция – деление некоторого (произвольного) количества гвоздей на две равные по весу кучки.
- 14. Задачи на переливание – это задачи, в которых с помощью сосудов известных ёмкостей требуется отмерить некоторое
- 15. Решение:
- 16. Задачи на установление взаимно однозначного соответствия между множествами данных множеств. Многие логические задачи связаны с рассмотрением
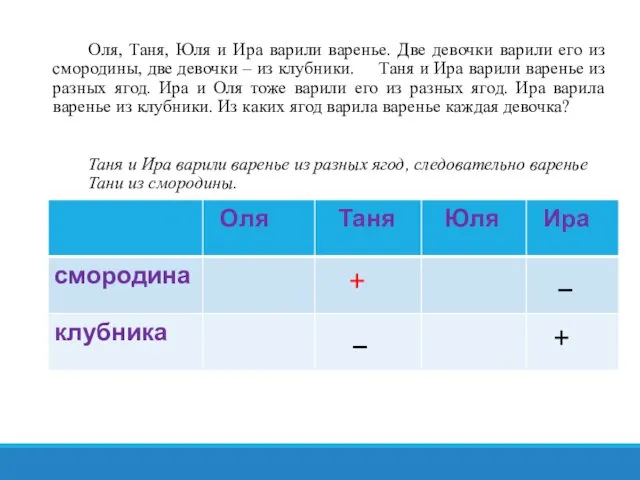
- 17. Задача: Оля, Таня, Юля и Ира варили варенье. Две девочки варили его из смородины, две девочки
- 18. Решение: 1. Составим таблицу 4 ∙ 2, т.к. было 4 девочки и 2 вида ягод.
- 19. Внимательно читаем условие задачи и начинаем расставлять соответствия. Оля, Таня, Юля и Ира варили варенье. Две
- 20. Оля, Таня, Юля и Ира варили варенье. Две девочки варили его из смородины, две девочки –
- 21. Ира и Оля тоже варили варенье из раз-ных ягод, значит Оля варила варенье из смородины.
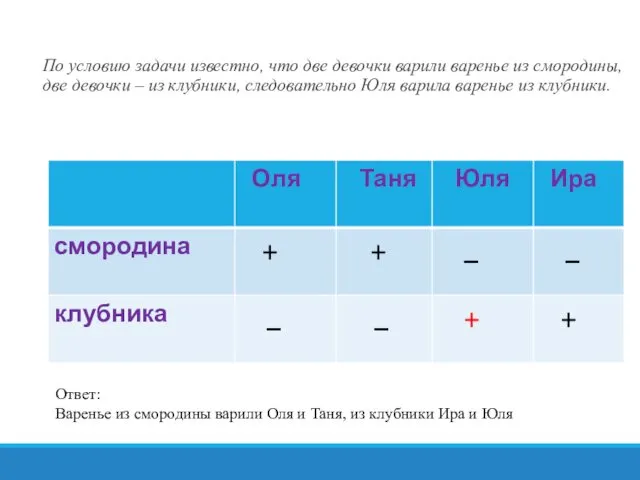
- 22. По условию задачи известно, что две девочки варили варенье из смородины, две девочки – из клубники,
- 23. Задачи: Наташа, Валя, Маша, Галя и Лена вырезали из бумаги разные фигуры. Кто-то вырезал круг из
- 24. Задачи, решаемые с «конца» Выделение данных задач в отдельную группу связано со способом рассуждения при решении,
- 25. Задача № 1: Я задумала число, умножила его на 7, прибавила 15 и получила 50. Какое
- 26. Задача № 2: Продавец, сидя на рынке, рассуждала: «Если к моим яблокам прибавить половину их да
- 27. Задачи: 1. Гуси. Над озерами летели гуси. На каждом озере садилась половина гусей и еще полгуся,
- 28. При решении различных математических задач применяется специальный метод, получивший название по имени немецкого математика: принцип Дирихле.
- 29. Принцип Дирихле́ («принцип ящиков») — утверждение, устанавливающее связь между объектами («кроликами») и контейнерами («клетками») при выполнении
- 30. Формулировки Наиболее распространена следующая формулировка этого принципа: Если в N клетках сидят не менее N +
- 31. Рассмотрим примеры различных задач, решаемых с помощью принципа Дирихле Задача № 1: В классе 15 учеников.
- 32. Задача № 2: В коробке лежат 5 карандашей: 2 синих и 3 красных. Сколько карандашей надо
- 33. Задачи: В классе 27 учеников. Найдется ли месяц, в котором отмечают свои дни рождения не меньше,
- 34. Задачи на установление взаимно однозначного соответствия между множествами Анализ условия задач данного вида приводит к необходимости
- 35. Задача №1 : У 10 велосипедов 27 колес. Сколько из этих велосипедов трехколесных и сколько двухколёсных?
- 36. Решение 1. Каждый велосипед обозначим чертой. Их 10 . 2. К каждому из них можно смело
- 37. Задача №2: У овец и кур вместе 36 голов и 100 ног. Сколько овец и сколько
- 38. Решение: В задаче не нарисуешь 36 голов, поэтому можно использовать схему, а решать по действиям. 1.
- 39. Задачи: 1. В клетке кролики и фазаны, всего 35 голов и 94 ноги. Сколько в клетке
- 40. Алгоритмическая задача «Переправа» Алгоритм – это понятное и точное предписание действий исполнителю, с целью получения результата
- 43. Задача №3
- 44. Комбинаторные задачи Комбинаторика - раздел математики, рассматривающий вопросы(задачи), связанные с подсчётом числа всевозможных комбинаций из элементов
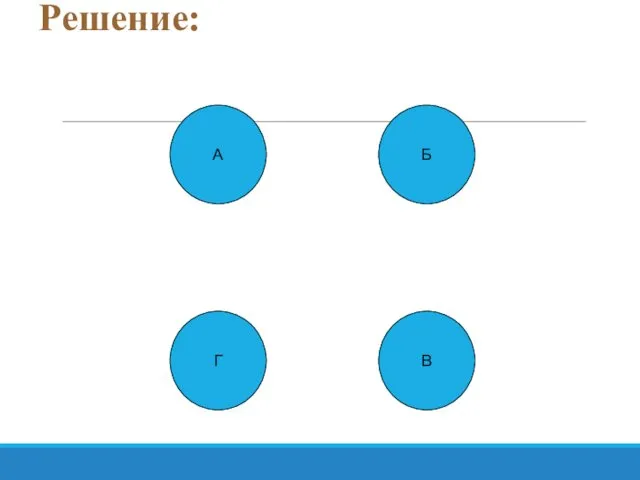
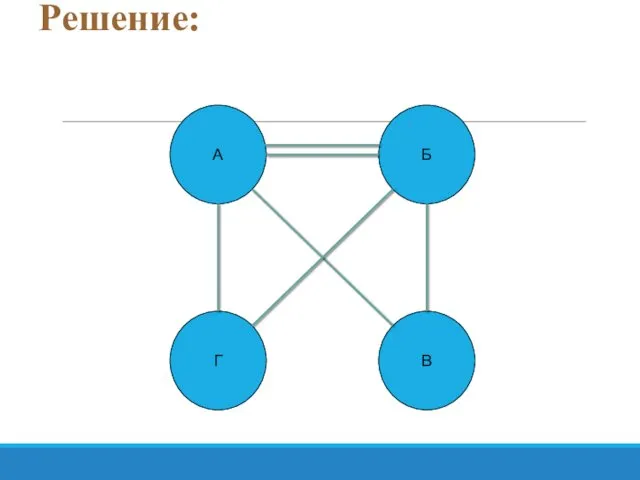
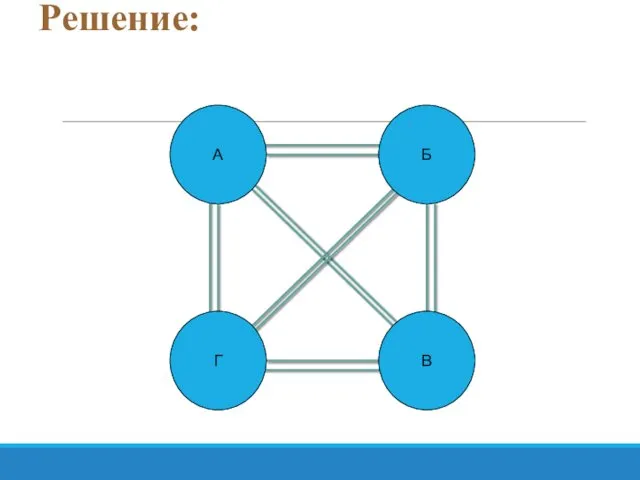
- 45. Задача №1 Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной
- 46. Решение: А Г Б В
- 47. Решение: А Г Б В
- 48. Решение: А Г Б В
- 49. Решение: Г Б В А
- 50. Решение: А Б Г В
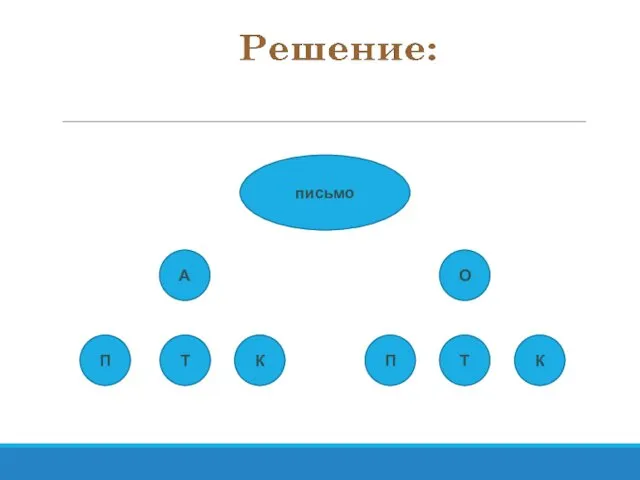
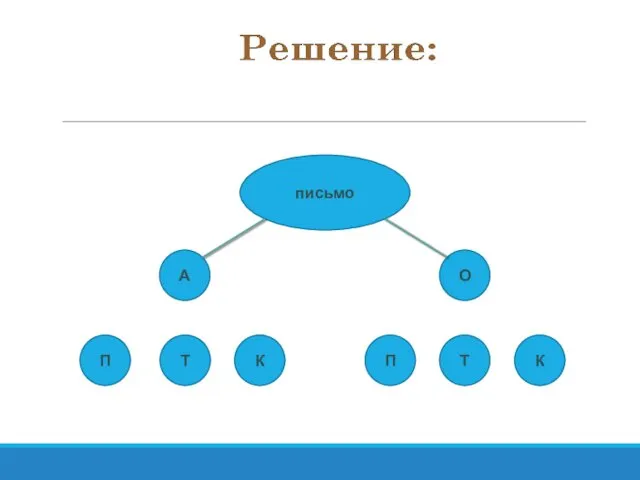
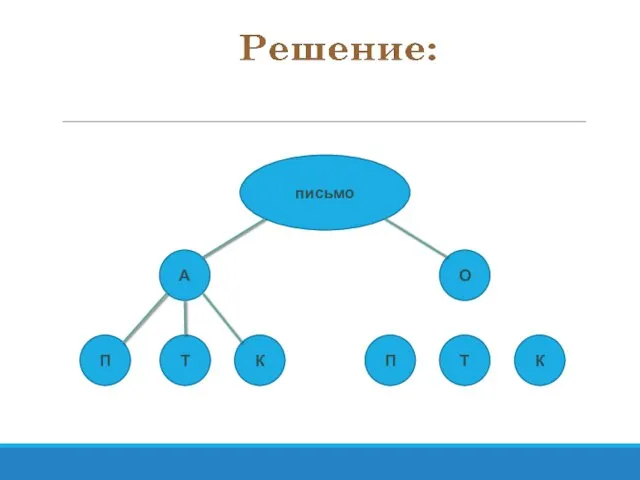
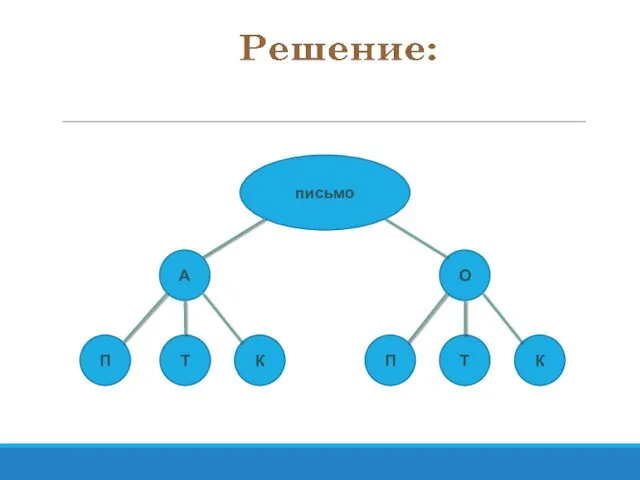
- 51. Задача №2 У Лёвы 2 конверта: обычный и авиа ,и 3 марки: прямоугольная , квадратная и
- 52. письмо А О П Т К П Т К
- 53. письмо А О П Т К П Т К
- 54. письмо А О П Т К П Т К
- 55. письмо А О П Т К П Т К
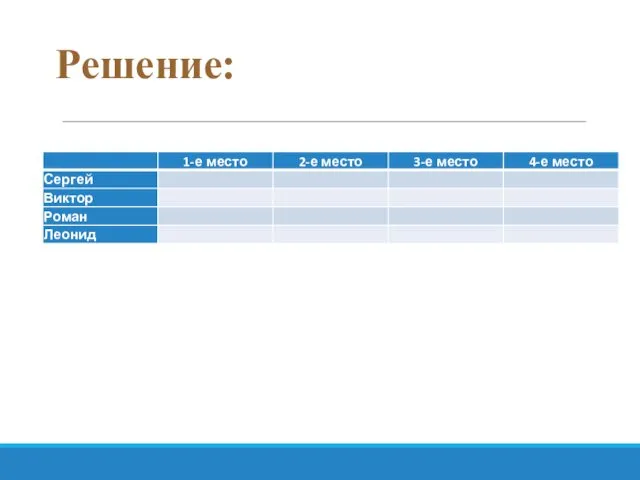
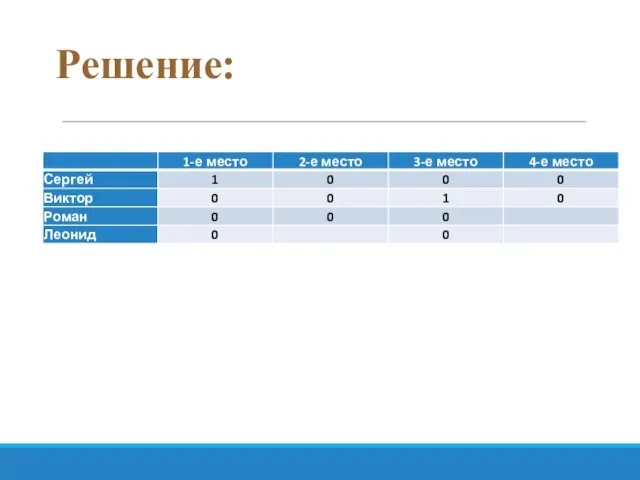
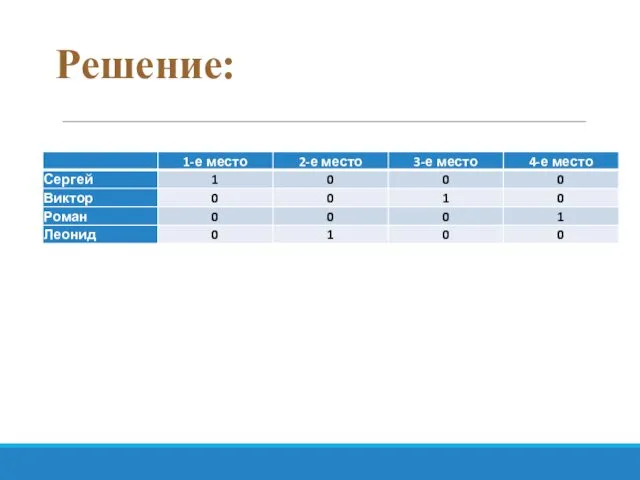
- 56. Задача №1 Виктор, Роман, Леонид и Сергей заняли на олимпиаде по информатике четыре первых места. Когда
- 57. Решение:
- 58. Решение:
- 59. Решение:
- 60. Решение:
- 61. Решение:
- 63. Скачать презентацию
















































 Координатная плоскость (урок математики в 6 классе) Кормачева Елена Владимировна, учитель математики МБОУ «Гимназия №11» Цен
Координатная плоскость (урок математики в 6 классе) Кормачева Елена Владимировна, учитель математики МБОУ «Гимназия №11» Цен Похідна та її застосування
Похідна та її застосування Теорема Пифагора и различные способы её доказательства
Теорема Пифагора и различные способы её доказательства Тест. Внетабличное умножение и деление. Деление с остатком
Тест. Внетабличное умножение и деление. Деление с остатком Шар. Объём шара
Шар. Объём шара Подготовительный этап к изучению нумерации чисел первого десятка
Подготовительный этап к изучению нумерации чисел первого десятка Презентация по математике "Тренажёр таблицы умножения и деления" - скачать бесплатно
Презентация по математике "Тренажёр таблицы умножения и деления" - скачать бесплатно Применение производной к решению задач ЕГЭ
Применение производной к решению задач ЕГЭ Исследование устойчивости особенной точки
Исследование устойчивости особенной точки Нелинейная регрессия
Нелинейная регрессия Решение задач на многогранники, цилиндр, конус, шар
Решение задач на многогранники, цилиндр, конус, шар Дискретные случайные величины
Дискретные случайные величины Уравнение. Дифференциальные уравнения первого порядка
Уравнение. Дифференциальные уравнения первого порядка Влияние музыки на развитие математических способностей
Влияние музыки на развитие математических способностей Метод контрольных вопросов
Метод контрольных вопросов Признаки равенства треугольников
Признаки равенства треугольников Первый признак равенства треугольников
Первый признак равенства треугольников Доказательство числовых неравенств
Доказательство числовых неравенств Параллельные прямые. Урок геометрии в 7 классе
Параллельные прямые. Урок геометрии в 7 классе Предел последовательности
Предел последовательности Задания по геометрии
Задания по геометрии 11 класс
11 класс  Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Умножение десятичных дробей
Умножение десятичных дробей Пересечение поверхности плоскостью
Пересечение поверхности плоскостью Деление с остатком
Деление с остатком Дискретная математика. Теория множеств
Дискретная математика. Теория множеств Решение тригонометрических и комбинированных уравнений
Решение тригонометрических и комбинированных уравнений