Содержание
- 2. Основные методы решения геометрических задач Метод дополнительных построений Метод геометрических преобразований Метод подобия Метод площадей Метод
- 3. Метод дополнительных построений Разновидности: Продолжение отрезка (отрезков) на определенное расстояние или до пересечения с заданной прямой
- 4. Метод геометрических преобразований Разновидности: центральная симметрия, осевая симметрия, параллельный перенос, поворот.
- 5. Метод площадей Один из алгоритмов решения многих геометрических задач основан на использовании свойств площадей фигур.
- 6. Метод вспомогательной окружности «Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии,
- 7. Метод геометрического видения Основывается на умениях видеть и сопоставлять геометрические факты. Обычно при решении не нужно
- 8. Метод координат Метод координат и векторный метод - самые универсальные методы геометрии. Главное - удачно выбрать
- 9. Векторный метод Типы задач, решаемых с помощью векторного метода: I тип – задачи, связанные с использованием
- 10. «Лучше решить задачу десятью способами, чем десять задач одним». Дьёрдь Пойя
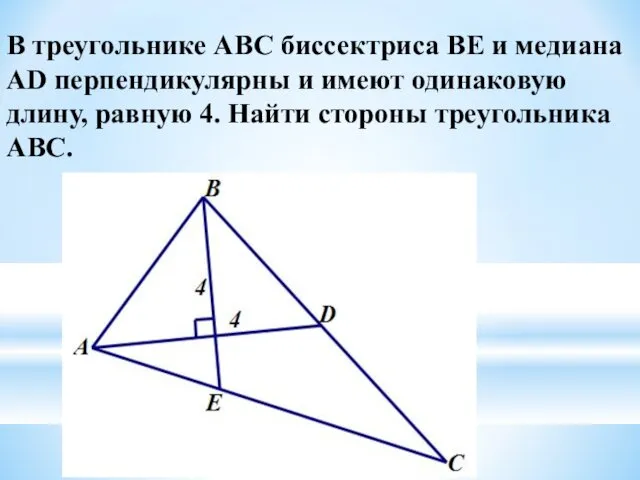
- 11. В треугольнике АВС биссектриса BЕ и медиана АD перпендикулярны и имеют одинаковую длину, равную 4. Найти
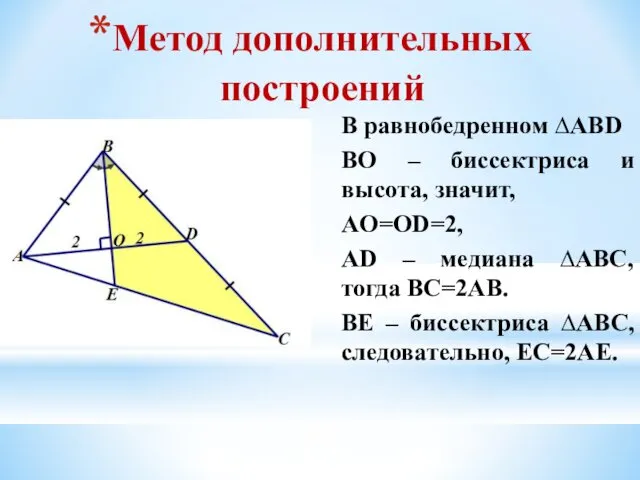
- 12. Метод дополнительных построений В равнобедренном ∆ABD BO – биссектриса и высота, значит, AO=OD=2, AD – медиана
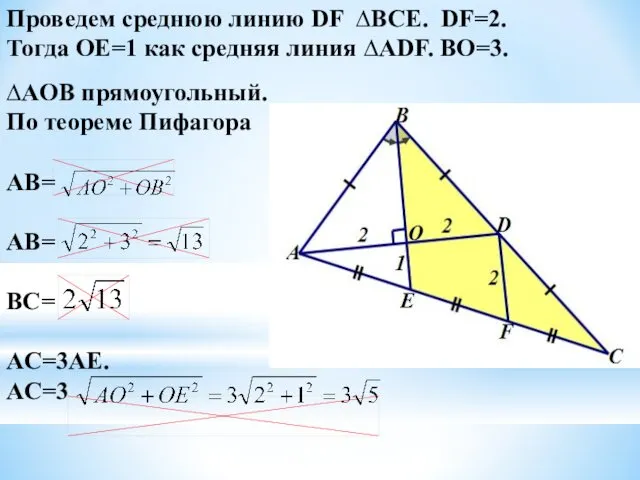
- 13. Проведем среднюю линию DF ∆BCE. DF=2. Тогда OE=1 как средняя линия ∆ADF. BO=3. ∆AOB прямоугольный. По
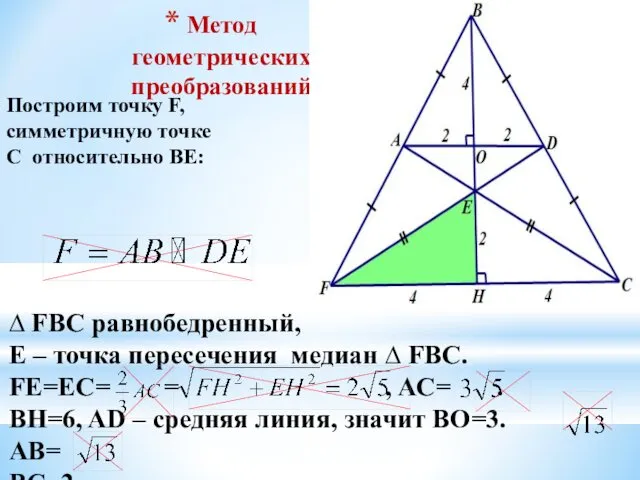
- 14. Метод геометрических преобразований Построим точку F, симметричную точке С относительно BE: ∆ FBC равнобедренный, Е –
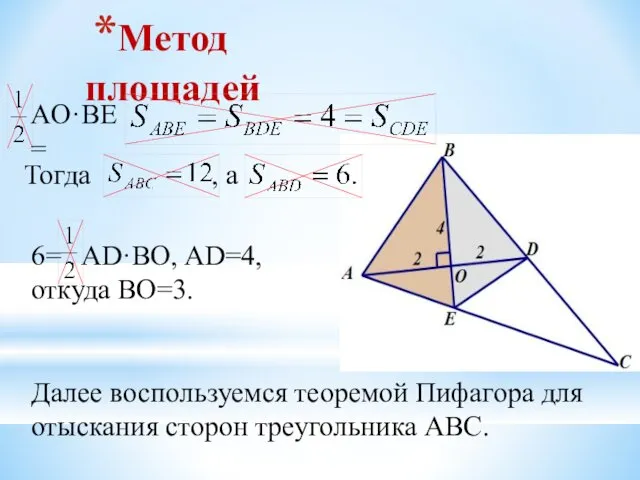
- 15. Метод площадей AO·BE= Тогда , а 6= AD·BO, AD=4, откуда BO=3. Далее воспользуемся теоремой Пифагора для
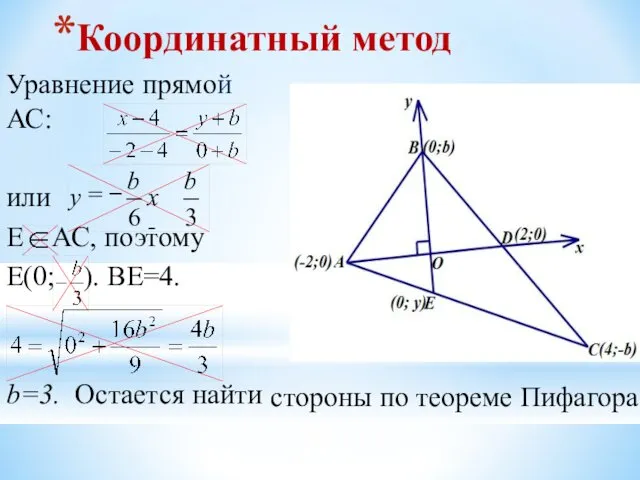
- 16. Координатный метод Уравнение прямой АС: или Е АС, поэтому Е(0; ). ВЕ=4. b=3. Остается найти стороны
- 18. Скачать презентацию









 Треугольник и его виды
Треугольник и его виды Математический кроссворд Сложение чисел в пределах 100
Математический кроссворд Сложение чисел в пределах 100 Аттестационная работа. Решение задач с помощью уравнений
Аттестационная работа. Решение задач с помощью уравнений Квадратные уравнения. Их решение по формуле
Квадратные уравнения. Их решение по формуле Полный стрелочный угол
Полный стрелочный угол Умножение обыкновенных дробей
Умножение обыкновенных дробей Движение протяженных тел
Движение протяженных тел Критерии надежности невосстанавливаемых систем. (Лекция 2)
Критерии надежности невосстанавливаемых систем. (Лекция 2) Презентация по математике "Математика в моей будущей профессии" - скачать
Презентация по математике "Математика в моей будущей профессии" - скачать  Не отрывая карандаша
Не отрывая карандаша Расстояния. Подготовка к ЕГЭ по математике 2019
Расстояния. Подготовка к ЕГЭ по математике 2019 Математические ребусы
Математические ребусы Решение неравенств
Решение неравенств Дроби и Проценты Зарецкий Ильяя 5а класс
Дроби и Проценты Зарецкий Ильяя 5а класс  Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости
Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости Комбинации тел с шаром
Комбинации тел с шаром Вычисление площадей с помощью интегралов
Вычисление площадей с помощью интегралов Дидактическая игра. Какого фрагмента не хватает на картинке (для дошкольников)
Дидактическая игра. Какого фрагмента не хватает на картинке (для дошкольников)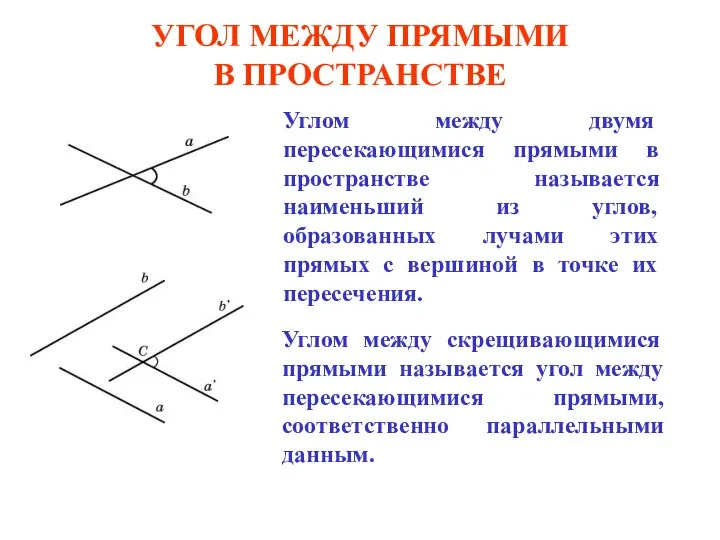 Угол между прямыми в пространстве
Угол между прямыми в пространстве Розробка та дослідження алгоритмів пошуку циклу Гамільтона на графі
Розробка та дослідження алгоритмів пошуку циклу Гамільтона на графі Применение координатно - векторного метода при решении задач
Применение координатно - векторного метода при решении задач Луч. Угол
Луч. Угол Линейная алгебра
Линейная алгебра Работа над ошибками к контрольной работе по теме: неравенства
Работа над ошибками к контрольной работе по теме: неравенства Применение параллелограмма
Применение параллелограмма Раскройте скобки
Раскройте скобки Сложение чисел с разными знаками
Сложение чисел с разными знаками Quantifiers
Quantifiers