Содержание
- 2. 7.1. Линейные уравнения Метод прямого перебора Использование неравенств Использование отношения делимости Метод «спуска» Использование формул 7.2.
- 3. Пример 74. В клетке сидят кролики и фазаны. Всего у них 18 ног. Узнать сколь- ко
- 4. Использование неравенств Пример 75. Решить в натуральных числах уравнение 5х + 8у = 39 Решение. Для
- 5. ИСПОЛЬЗОВАНИЕ ОТНОШЕНИЯ ДЕЛИМОСТИ Пример 76. Имеются контейнеры двух видов: по 130 кг и 160 кг. Сколько
- 6. МЕТОД «СПУСКА» Пример 79. Решить в целых числах уравнение 5х - 7у = 3. Решение. Выразим
- 7. Использование формул Теорема. Уравнение a1x1 + a2x2 + … + anxn = b разрешимо в целых
- 8. Пример 81. (МГУ, 1969). Остаток от деления некоторого натурального числа n на 6 равен 4, остаток
- 9. Пример 83. Решить в целых числах уравнение 127x - 52y + 1 = 0. Решение. Преобразуем
- 10. Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби
- 11. 7.2. Нелинейные уравнения Метод разложения на множители вынесение общих множителей за скобку Пример 84. Решить в
- 12. ПРИМЕНЕНИЕ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ Пример 85. Найти все пары натуральных чисел, разность квадратов которых равна 55.
- 13. Использование параметра Пример 88. Решить в целых числах уравнение 2x2 - 2yx + 9x + y
- 14. Метод решения относительно одной переменной выделение целой части Пример 89. (МГУ, 1997). Найти все пары целых
- 15. Метод «спуска» метод конечного «спуска» Пример 96. Решить в целых числах уравнение 2x2 - 5y2 =
- 16. Поскольку числа 3у и 14 – целые, то 3x +17 должно быть делителем числа 25: 3x
- 17. Параметризация уравнения Пример 99. Решить в целых числах уравнение x3 + y3 + z3 = 2.
- 18. Функционально-графический метод Пример 100. (МИОО 2010). Найти все пары натуральных k и n таких, что k
- 19. откуда следует k = 1 или , k = 2, причем для каждого k может найтись
- 20. 7.3. Неравенства Использование области определения Пример 102. (МГУ, 1973). Найти все целые числа x , удовлетворяющие
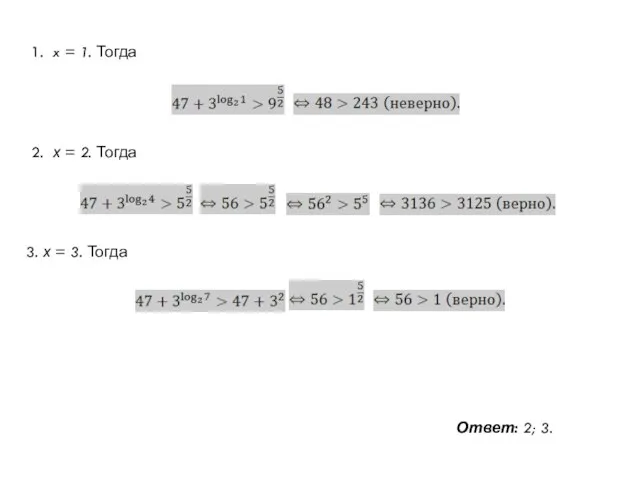
- 21. 1. x = 1. Тогда 2. х = 2. Тогда 3. х = 3. Тогда Ответ:
- 22. Использование монотонности Пример 103. (МГУ, 1976). Найти все целые z, удовлетворяющие неравенству Решение. Допустимые значения z
- 23. Использование ограниченности Пример 104. (МГУ, 1996). Найти все целочисленные решения неравенства Решение. Целые решения будем искать
- 24. Метод интервалов Пример 105. (МГУ, 1972). Определить, сколько целочисленных решений имеет неравенство Решение. Методом интервалов по
- 25. 7.4. Уравнения и неравенства Уравнение с одной неизвестной Пример 107. Может ли квадратное уравнение ax2 +
- 26. Показательные уравнения Теорема. Если остаток от деления a1 на b равен r1, а остаток от деления
- 27. Неравенства Пример 121. (МИОО 2010). Найти все пары (x; y) целых чисел, удовлетворяющие системе неравенств: Решение.
- 29. Скачать презентацию

























 Длина окружности
Длина окружности Иррациональные уравнения
Иррациональные уравнения Компланарные векторы
Компланарные векторы 1.Способ неопределенных коэффициентов для нахождения частного решения неопределенного линейного уравнения.
1.Способ неопределенных коэффициентов для нахождения частного решения неопределенного линейного уравнения.  Смешанные числа
Смешанные числа Числовые функции
Числовые функции Построение окружности по точкам
Построение окружности по точкам Представление двузначных чисел в виде различных слагаемых
Представление двузначных чисел в виде различных слагаемых Понятие тетраэдра
Понятие тетраэдра Понятие угла. Радианная мера угла
Понятие угла. Радианная мера угла logarifmy_111.pptx_9d08dc30-484f-4528-bf9f-7ed41df5987a (2)
logarifmy_111.pptx_9d08dc30-484f-4528-bf9f-7ed41df5987a (2) Презентация по математике "Системы уравнений" - скачать бесплатно
Презентация по математике "Системы уравнений" - скачать бесплатно Объемы. Соотношения между единицами объема
Объемы. Соотношения между единицами объема Вычислить интеграл от функции комплексного переменного по данной кривой
Вычислить интеграл от функции комплексного переменного по данной кривой Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Теорема о вписанном угле. (8 класс)
Теорема о вписанном угле. (8 класс) Множества. Операции над множествами
Множества. Операции над множествами Предел функции
Предел функции Лесная школа. Табличное умножение
Лесная школа. Табличное умножение Cálculo numérico. Resolução de equações diferenciais ordinárias de 1a ordem. (Aula 9)
Cálculo numérico. Resolução de equações diferenciais ordinárias de 1a ordem. (Aula 9) Геометрия. 7 класс. Измерение отрезков и углов
Геометрия. 7 класс. Измерение отрезков и углов Квадратичные функции
Квадратичные функции Скалярное и векторное произведения векторов
Скалярное и векторное произведения векторов Аттестационная работа. Организация познавательной деятельности школьников через систему внеклассной работы по математике
Аттестационная работа. Организация познавательной деятельности школьников через систему внеклассной работы по математике Числовая окружность
Числовая окружность Векторы. Тест. (Вариант 1)
Векторы. Тест. (Вариант 1) Таблица сложения однозначных чисел. 1 класс
Таблица сложения однозначных чисел. 1 класс Кореляція. Лінійна регресія
Кореляція. Лінійна регресія