Содержание
- 2. Точка (х0,у0) называется точкой условного экстремума (максимума или минимума), если существует такая окрестность этой точки, что
- 3. Чтобы найти условный экстремум, нужно из уравнения связи выразить одну переменную через другую: y=φ(x). Подставим это
- 4. безусловный экстремум условный экстремум
- 5. ПРИМЕР. Найти точки максимума и минимума функции при условии 3х+2у=11.
- 6. РЕШЕНИЕ.
- 7. В этом примере связь между х и у оказалась линейной, поэтому уравнение связи легко разрешилось относительно
- 8. функция Лагранжа
- 9. ТЕОРЕМА. Если точка (х0,у0) является точкой условного экстремума функции z=f(x,y) при условии g(x,y)=C, то существует значение
- 10. Следовательно, для нахождения условного экстремума функции z=f(x,y) при условии g(x,y)=C, требуется найти решение системы:
- 11. Последнее уравнение совпадает с уравнением связи. Первые два уравнения можно записать в виде: То есть в
- 13. Скачать презентацию




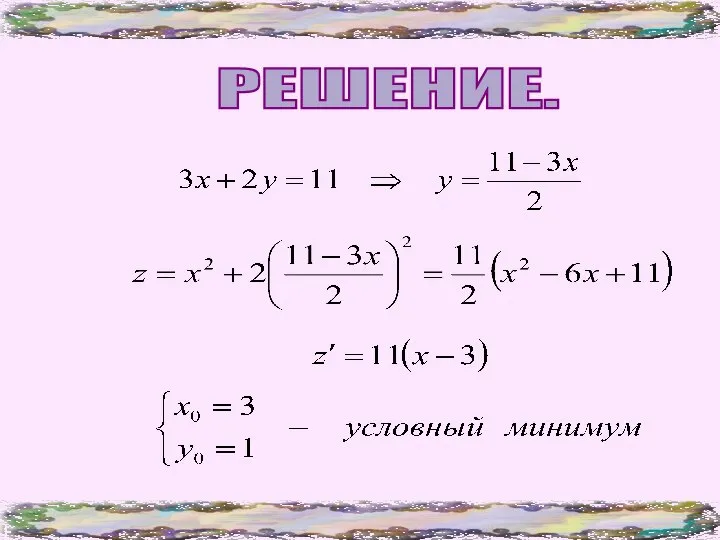





 Комплексные числа
Комплексные числа Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теория Множеств
Теория Множеств Метод анализа иерархий. Методика метода МАИ
Метод анализа иерархий. Методика метода МАИ Аттестационная работа. Элективный курс в 5 классе по математике: Проект Вологда в задачах
Аттестационная работа. Элективный курс в 5 классе по математике: Проект Вологда в задачах Производная показательной функции
Производная показательной функции Обобщающий урок по теме: «Уравнения»
Обобщающий урок по теме: «Уравнения» Морфрлогический анализ
Морфрлогический анализ Площадь и объем призмы. Задачи по теме
Площадь и объем призмы. Задачи по теме Треугольник. Определение. Виды треугольников
Треугольник. Определение. Виды треугольников Статистический анализ зависимостей между гидрологическими переменными (лекция 10)
Статистический анализ зависимостей между гидрологическими переменными (лекция 10) Сложение смешанных дробей
Сложение смешанных дробей Решение уравнений, приводимых к квадратным
Решение уравнений, приводимых к квадратным Порівняння декількох (трьох і більше) груп даних
Порівняння декількох (трьох і більше) груп даних Готфрид Вильгельм Лейбниц (1646-1716)
Готфрид Вильгельм Лейбниц (1646-1716) Осевая и центральная симметрии
Осевая и центральная симметрии Задачи на смекалку
Задачи на смекалку Сложение натуральных чисел и его свойства
Сложение натуральных чисел и его свойства Порядок действий в выражениях без скобок
Порядок действий в выражениях без скобок Число 19
Число 19 Решение задач по теме «Равнобедренный треугольник»
Решение задач по теме «Равнобедренный треугольник» Қаржы-несие шешімдерін қабылдауға қаржы-экономикалық есептеудің математикалық негіздері
Қаржы-несие шешімдерін қабылдауға қаржы-экономикалық есептеудің математикалық негіздері Символы математической логики
Символы математической логики Ум заключается не только в знании, но и в умении прилагать знание в дело Аристотель
Ум заключается не только в знании, но и в умении прилагать знание в дело Аристотель  Смешанные числа
Смешанные числа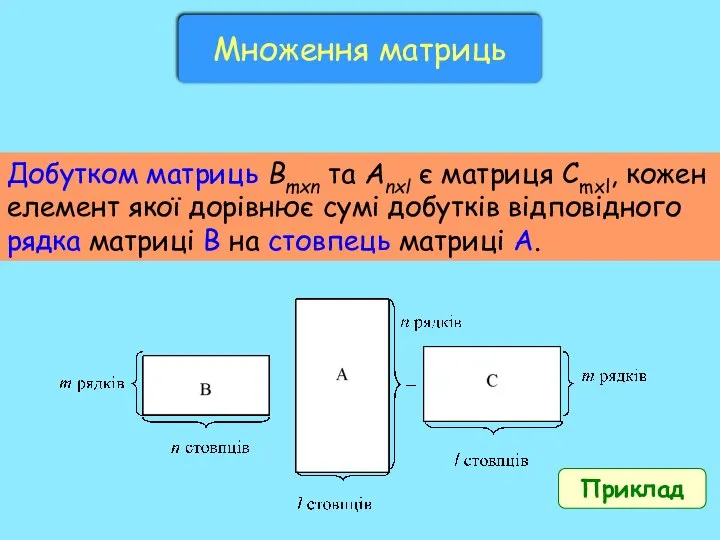 Множення матриць
Множення матриць Основные темы курса: Теория множеств, теория вероятности, элементы комбинаторики, элементы статистики
Основные темы курса: Теория множеств, теория вероятности, элементы комбинаторики, элементы статистики Тренировочный тест. Значение выражений
Тренировочный тест. Значение выражений