Непрерывно-детерминированные, дискретнодетерминированные, дискретно-вероятностные и непрерывно-вероятностные модели
Содержание
- 2. Как известно, величины могут быть двух типов — дискретные, т. е. принимающие «оторванные» друг от друга
- 4. Непрерывно-детерминированные, дискретно-детерминированные, дискретно-вероятностные и непрерывно-вероятностные модели. Вебинар № 5 Непрерывные модели. Дискретные модели. Стохастические модели
- 5. Модели — как содержательные, так и математические — могут быть либо дискретными, либо непрерывными, либо смешанными.
- 6. Будем предполагать, что возможно, хотя бы в принципе, установить и на некотором языке описания (например, средствами
- 7. Пусть М=М(X,Y,Z), где X – множество входов, Y – выходов, Z – состояний системы. Схематически можно
- 8. Непрерывность и дискретность. Все те объекты, переменные которых (включая, при необходимости, время) могут принимать несчетное множество
- 9. Свойство непрерывности и дискретности выражается в структуре множеств (совокупностей), которым принадлежат параметры состояния, параметр процесса и
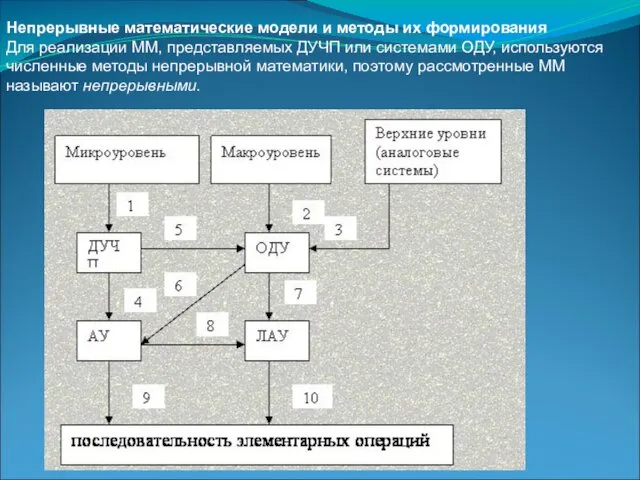
- 10. Непрерывные математические модели и методы их формирования Для реализации ММ, представляемых ДУЧП или системами ОДУ, используются
- 11. На рис. оказаны преобразования непрерывных ММ в процессе перехода от исходных формулировок задач к рабочим программам,
- 12. Непрерывные ММ и используемые для их анализа методы вычислительной математики получили широкое распространение в САПР различных
- 13. Дискретные математические модели. Дискретной математической моделью называется модель, в которой выполнена дискретизация тех или иных переменных.
- 14. На системном уровне проектирования систем преимущественно распространены модели систем массового обслуживания (СМО). Для таких моделей характерно
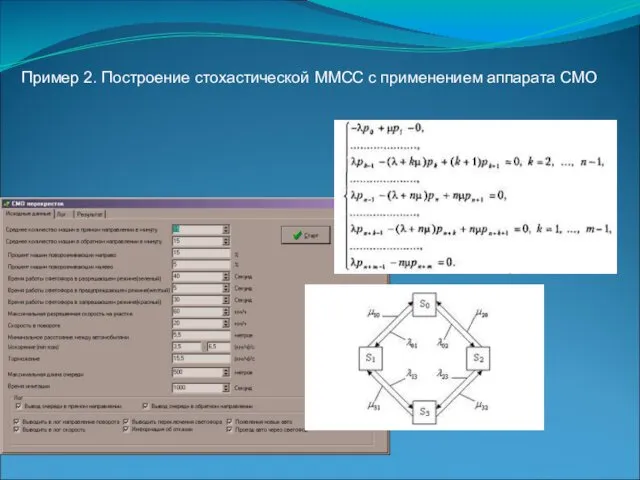
- 15. Пример 2. Построение стохастической ММСС с применением аппарата СМО
- 16. Появление параллельных и конвейерных систем, необходимость моделировать процессы функционирования не только аппаратных, но и программных средств
- 17. В комбинированных дискретно-непрерывных моделях независимые переменные могут изменяться как дискретно, так и непрерывно. В рамках методологии
- 18. СТОХАСТИЧЕСКАЯ МОДЕЛЬ [stochastic model] — такая экономико-математическая модель, в которой параметры, условия функционирования и характеристики состояния
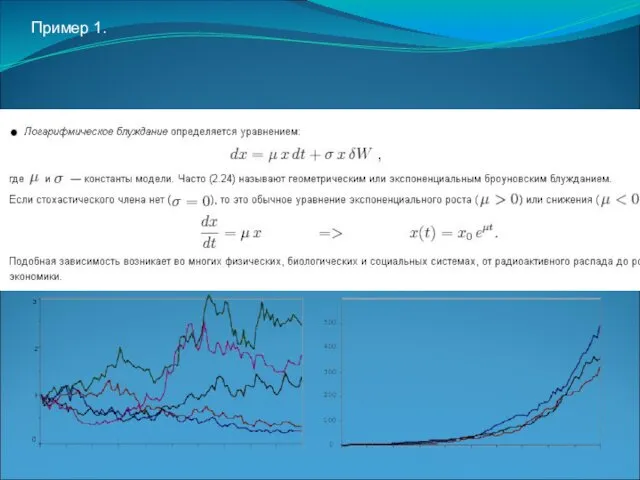
- 19. Пример 1.
- 20. Автор: Орлова И.В., Половников В.А. Издательство: Вузовский учебник Год: 2008 В.В. Васильев, Л.А. Симак, А.М. Рыбникова.
- 22. Скачать презентацию














![СТОХАСТИЧЕСКАЯ МОДЕЛЬ [stochastic model] — такая экономико-математическая модель, в которой параметры,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/447401/slide-17.jpg)

 Квадрат и куб числа
Квадрат и куб числа Презентация "Решение уравнений (6 класс)" - скачать
Презентация "Решение уравнений (6 класс)" - скачать  Презентация по математике Отношения и пропорции
Презентация по математике Отношения и пропорции  Параллельность прямых и плоскостей. Задания для устного счета. Упражнение 2
Параллельность прямых и плоскостей. Задания для устного счета. Упражнение 2 Деление обыкновенных дробей. Устная работа
Деление обыкновенных дробей. Устная работа Первый урок математики в 6 классе
Первый урок математики в 6 классе Классическая линейная регрессия
Классическая линейная регрессия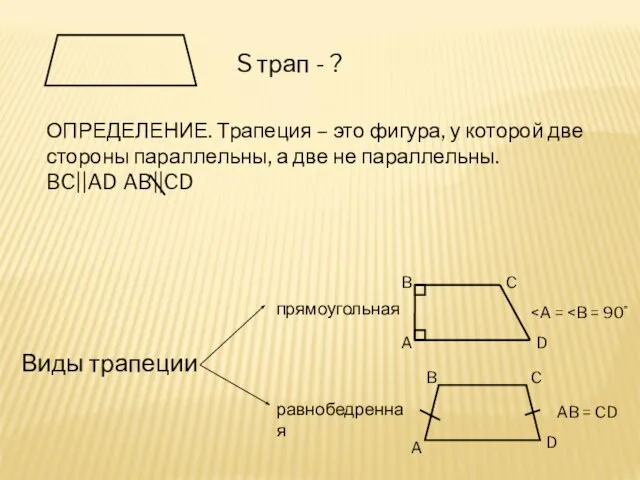 Площадь трапеции
Площадь трапеции Урок математики, 2 класс «Проверка вычитания»
Урок математики, 2 класс «Проверка вычитания» Координаты вектора
Координаты вектора Урок математики «Деление»
Урок математики «Деление»  Признаки равенства треугольников
Признаки равенства треугольников Математика 3 класс.
Математика 3 класс.  Анализируем результаты ЕГЭ 15, готовимся к ЕГЭ 16
Анализируем результаты ЕГЭ 15, готовимся к ЕГЭ 16 Презентация по математике "Состав чисел 12, 13" - скачать
Презентация по математике "Состав чисел 12, 13" - скачать  Обыкновенные дроби. 6 класс
Обыкновенные дроби. 6 класс Прямоугольный треугольник и его свойства. Единственность перпендикуляра к прямой
Прямоугольный треугольник и его свойства. Единственность перпендикуляра к прямой Теория матричных игр
Теория матричных игр Многоугольники
Многоугольники Скалярное произведение векторов. Угол между векторами
Скалярное произведение векторов. Угол между векторами Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ
Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ Логческие задачи
Логческие задачи Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки
Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки Математика. Основы школьного стандарта
Математика. Основы школьного стандарта Решение уравнений: Нахождение неизвестных делителя и делимого. 6 класс
Решение уравнений: Нахождение неизвестных делителя и делимого. 6 класс Смежные, вертикальные углы
Смежные, вертикальные углы Основы теории вероятностей
Основы теории вероятностей Выпуклый анализ. Связь между выпуклыми функциями и выпуклыми множествами. Лекция 14
Выпуклый анализ. Связь между выпуклыми функциями и выпуклыми множествами. Лекция 14