Несобственные интегралы. Функции нескольких переменных: область определения, линии уровня, частные производные
Содержание
- 2. В определении предполагается, что - конечные числа, а - непрерывная функция. Если хотя бы одно из
- 3. Мы рассмотрим интегралы по бесконечному промежутку или несобственные интегралы 1-ого рода: Если такой предел существует и
- 4. Если же указанный предел не существует или бесконечен, то говорят, что интеграл расходится. Аналогично определяется где
- 5. Пример. следовательно сходится.
- 6. На практике при вычислении несобственных интегралов можно сразу применять формулу Ньютона-Лейбница и символ « » подставлять
- 7. сходится, Теорема. расходится.
- 8. Пример. Площадь прямоугольника со сторонами находится по формуле Функция двух переменных Эта формула определяет функцию двух
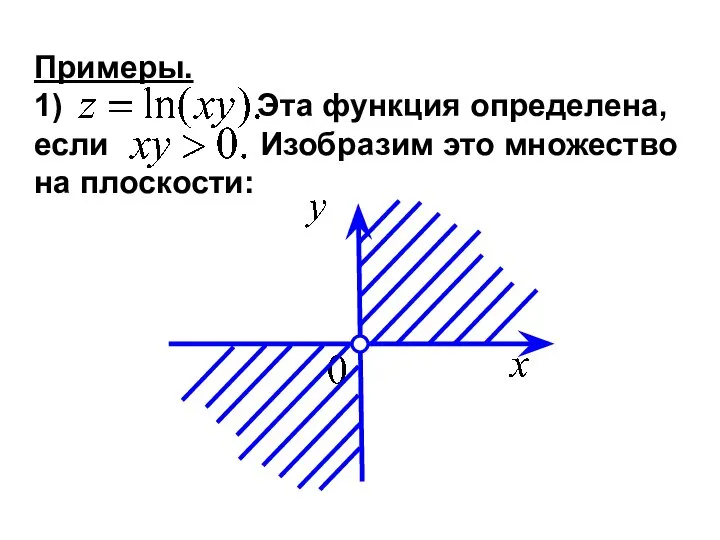
- 9. Примеры. 1) Эта функция определена, если Изобразим это множество на плоскости:
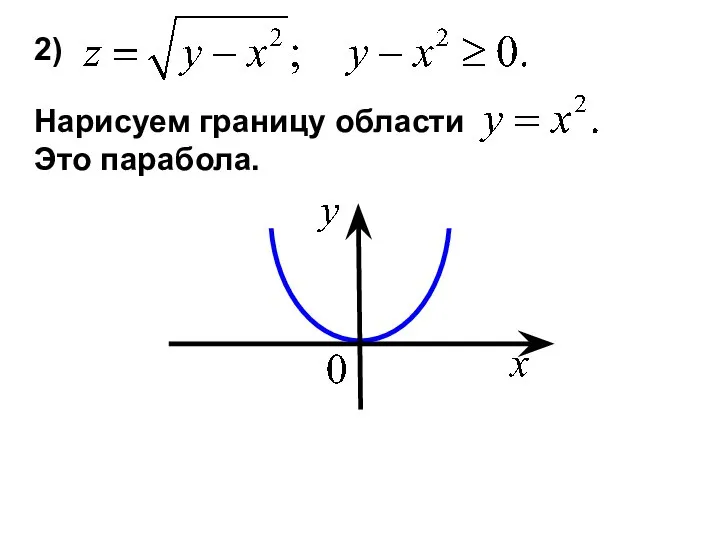
- 10. 2) Нарисуем границу области Это парабола.
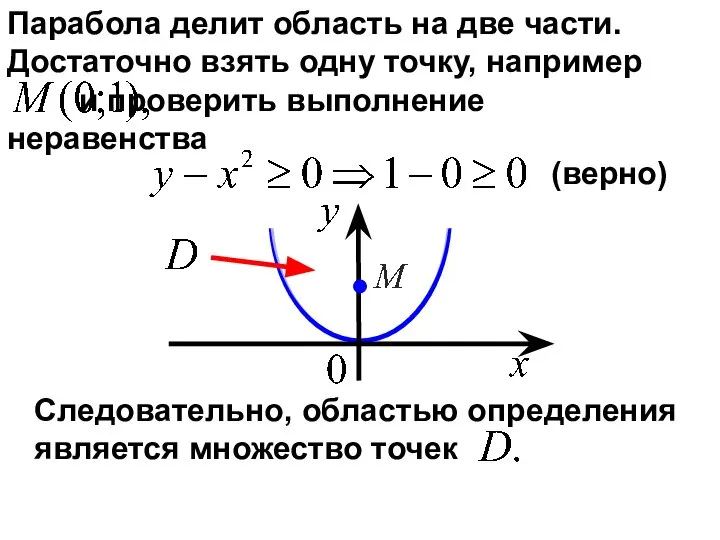
- 11. Парабола делит область на две части. Достаточно взять одну точку, например и проверить выполнение неравенства (верно)
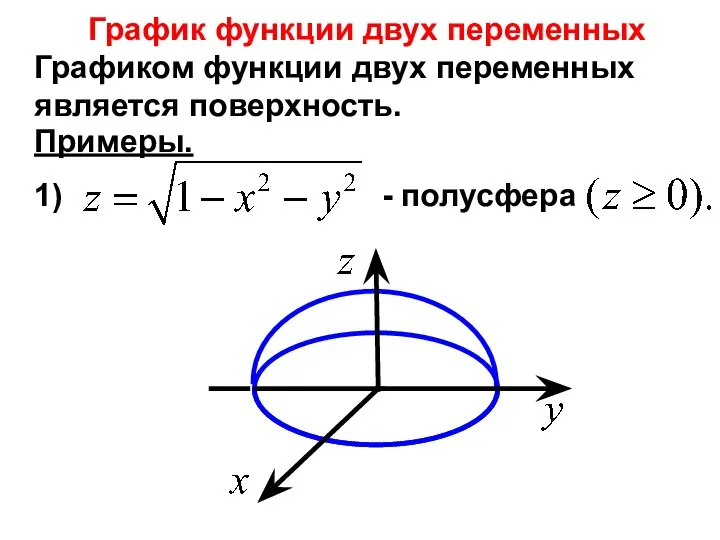
- 12. Графиком функции двух переменных является поверхность. График функции двух переменных Примеры. 1) - полусфера
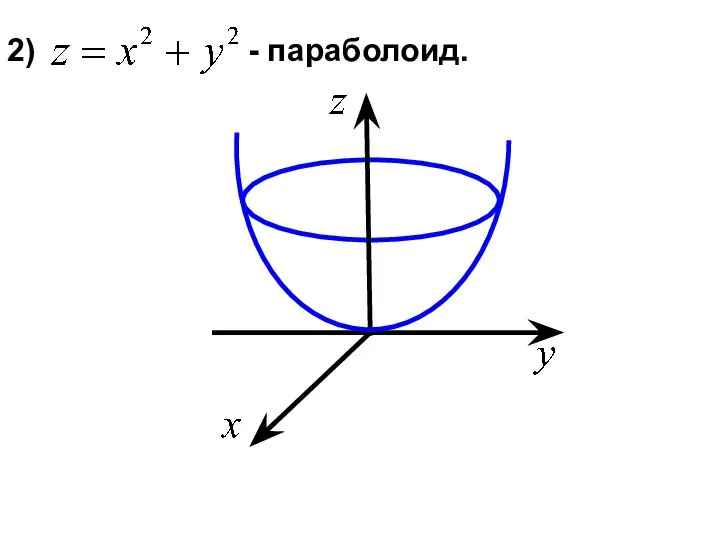
- 13. 2) - параболоид.
- 14. Построение графиков функций двух переменных представляет значительные трудности. Поэтому существует еще один способ изображения функции двух
- 15. Назовем линией уровня множество точек плоскости где - число. Термин «линии уровня» взят из картографии. Там
- 16. Пример. Построить линии уровня функции Линии уровня определяются уравнением Давая различные значения, получаем семейство концентрических окружностей.
- 17. (радиус )
- 18. Рассмотрим функцию Зафиксируем одну переменную, например, Пусть Тогда получится функция одной переменной Производная от такой функции
- 19. Пример. 1) Найти и если
- 20. Функция имеет четыре частные производные второго порядка. Частные производные 2-ого порядка и называются смешанными производными.
- 21. Теорема. Смешанные производные и равны между собой при условии их непрерывности:
- 22. Пример. 1) Найти частные производные второго порядка функции
- 23. Мы видим, что
- 24. Пусть Полный дифференциал Полный дифференциал функции Пример. Найти
- 25. Пусть причем Тогда есть сложная функция одной переменной Дифференцирование сложных функций
- 26. Рассмотрим теперь функцию при условии, что Здесь переменная есть функция одной переменной Этот случай сводится к
- 27. Но - частная производная, которая находится так, как если бы не зависел от .
- 28. - производная сложной функции одной переменной. Эту производную называют полной производной.
- 29. где Найти и Примеры. 1) Затем вместо подставим Получим
- 30. Ответ: 2)
- 32. Скачать презентацию
















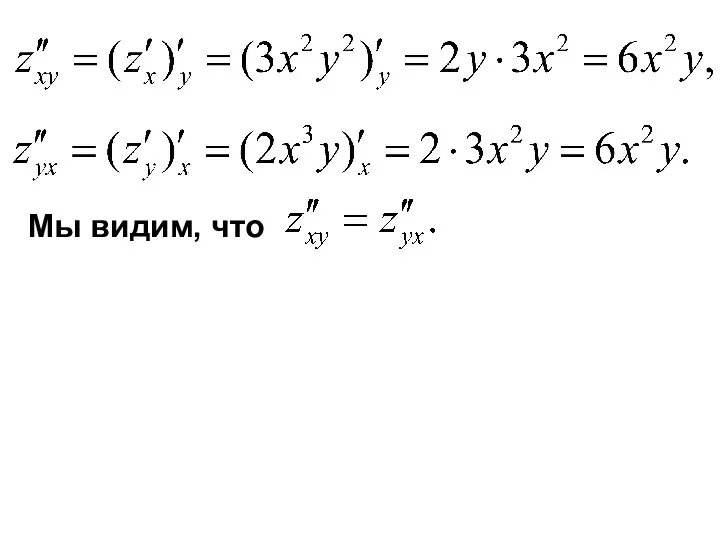






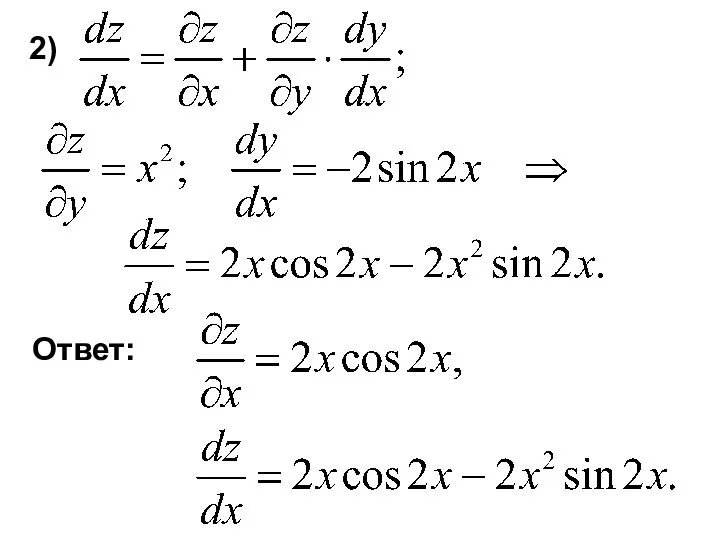
 Столбчатые диаграммы и графики
Столбчатые диаграммы и графики Сложение и вычитание многозначных чисел. Закрепление. Деловая игра. 4 класс
Сложение и вычитание многозначных чисел. Закрепление. Деловая игра. 4 класс Группировки в историческом исследовании. (Лекция 2)
Группировки в историческом исследовании. (Лекция 2) Сложение и вычитание многозначных чисел
Сложение и вычитание многозначных чисел  Inscribed and circumscribed circles of a triangle
Inscribed and circumscribed circles of a triangle Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Задачи на построение
Задачи на построение Обработка многократно измеренных величин
Обработка многократно измеренных величин Моделирование алгоритмов вейвлет-преобразования. Матрица гармонического вейвлет-преобразования
Моделирование алгоритмов вейвлет-преобразования. Матрица гармонического вейвлет-преобразования Презентация на тему Обозначение натуральных чисел 5 класс
Презентация на тему Обозначение натуральных чисел 5 класс Решение дробных рациональных уравнений. 8 класс
Решение дробных рациональных уравнений. 8 класс Первообразная и интеграл
Первообразная и интеграл Приближенное вычисление интегралов (тема 9)
Приближенное вычисление интегралов (тема 9) Построение треугольника по трем элементам
Построение треугольника по трем элементам Развитие пространственного мышления с опорой на наглядно-образное мышление. Разрезные фигуры
Развитие пространственного мышления с опорой на наглядно-образное мышление. Разрезные фигуры Презентация по математике "Метод математической индукции" - скачать бесплатно
Презентация по математике "Метод математической индукции" - скачать бесплатно Математическая викторина
Математическая викторина Урок геометрии 8 класс
Урок геометрии 8 класс Мәйданнарны үлчәү берәмлекләре
Мәйданнарны үлчәү берәмлекләре Число π (пи)
Число π (пи) Числа 1 – 5 закрепление
Числа 1 – 5 закрепление Прибавить и вычесть число 1
Прибавить и вычесть число 1 Решение практико-ориентированных задач
Решение практико-ориентированных задач Наши истинные учителя опыт и чувства. Из истории геометрии
Наши истинные учителя опыт и чувства. Из истории геометрии Математика XIX ст. Жан Батист Жозеф Фур'є
Математика XIX ст. Жан Батист Жозеф Фур'є Скорость движения
Скорость движения Числовые последовательности
Числовые последовательности Основные понятия алгебры логики
Основные понятия алгебры логики