Содержание
- 2. Обработка многократно измеренных величин Исследование на нормальность: 1. Предварительные исследования (грубость, систематика – условия Ляпунова –
- 3. Обработка многократно измеренных величин Суть критерия Пирсона: Подсчет разности практических и теоретических относительный частот, попавших в
- 4. Обработка многократно измеренных величин Случайность – параметрический подход Неслучайность -линейный тренд - систематика. Критерий коэффициентов регрессии.
- 5. Обработка многократно измеренных величин Решить нормальные уравнения относительно а и b В матричном виде Лучшая вычислительная
- 6. Обработка многократно измеренных величин Составляем матрицу нормальных уравнений N и вектор с для системы нормальных уравнений
- 7. Обработка многократно измеренных величин Случайность – непараметрический подход – мало измерений, неизвестен закон распределения измерений Лучший
- 8. Обработка многократно измеренных величин Проверка однородности результатов измерений. Общий случай - сравнение законов распределений между собой
- 9. Обработка многократно измеренных величин Параметрические и непараметрические методы. Основой проверки на грубые измерения нормальная метка (z-метка)
- 10. Обработка многократно измеренных величин Критерий Романовского – вычисление характеристик без подозреваемых: Неравенство выполняется – крайние грубые.
- 11. Обработка многократно измеренных величин Непараметрические методы оценивания грубых погрешностей – устойчивые оценки сдвига и масштаба –
- 12. Обработка многократно измеренных величин F-1(р) - квантиль нормального закона распределения для вероятности р. Взяв вероятность 0.999
- 13. Обработка многократно измеренных величин Проверка ряда измерений на однородность по главным характеристикам. Делят на 2 или
- 14. Обработка многократно измеренных величин Неравноточность дисперсий по критерию Фишера разбиением выборки на 2 подвыборки. Статистика Если
- 15. Обработка многократно измеренных величин Непараметрические критерии - закон распределения не известен, мало измерений. Основной - критерий
- 16. Обработка многократно измеренных величин Для устойчивости - ранговый коэффициент корреляции Спирмена. Реализация критерия: - получаем оценки
- 17. Обработка многократно измеренных величин Окончание критерия - оценка отличия от нуля коэффициента корреляции между номером элемента
- 18. Обработка многократно измеренных величин Исследование на независимость элементов в ряде измерений. Предполагает отсутствие значимой связи между
- 19. Обработка многократно измеренных величин – используя любой способ строят линейную модель для ряда измерений, чаще вида
- 20. Обработка многократно измеренных величин Анализ результатов тестирования (см. формулы выше): если ≈ 0 (отсутствие автокорреляции), то
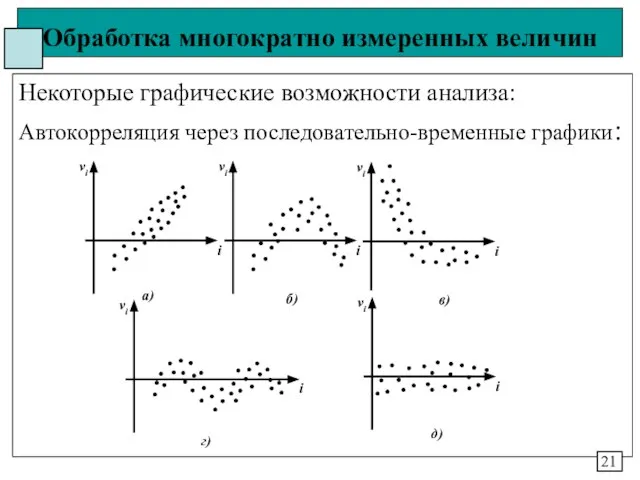
- 21. Обработка многократно измеренных величин Некоторые графические возможности анализа: Автокорреляция через последовательно-временные графики: 21
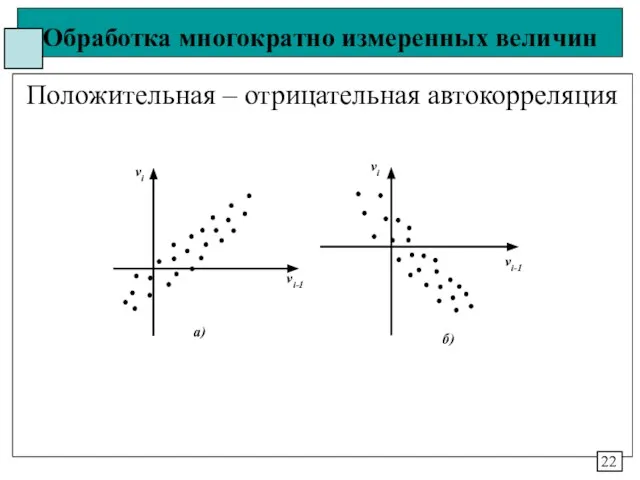
- 22. Обработка многократно измеренных величин Положительная – отрицательная автокорреляция 22
- 24. Скачать презентацию



















 Математика и спорт
Математика и спорт Системи комп’ютерної математики
Системи комп’ютерної математики Аттестационная работа. Эссе. Проектно-исследовательская деятельность на уроках математики в условиях реализации ФГОС
Аттестационная работа. Эссе. Проектно-исследовательская деятельность на уроках математики в условиях реализации ФГОС Синус, косинус и тангенс углов от 0⁰ до 180 ⁰
Синус, косинус и тангенс углов от 0⁰ до 180 ⁰ Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Аксиомы стереометрии 10 класс
Аксиомы стереометрии 10 класс Тренажёр. Таблица умножения. «Юные водители»
Тренажёр. Таблица умножения. «Юные водители» Углы. Повторение
Углы. Повторение Таблица умножения и деления на 9
Таблица умножения и деления на 9 Синус, косинус, тангенс острого угла прямоугольного треугольника
Синус, косинус, тангенс острого угла прямоугольного треугольника Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Көп айнымалылар функциясы
Көп айнымалылар функциясы П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах
П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах Презентация по математике "Знакомьтесь, уравнение" - скачать
Презентация по математике "Знакомьтесь, уравнение" - скачать  Цементы для временной фиксации
Цементы для временной фиксации  Десятичные дроби и метрическая система мер
Десятичные дроби и метрическая система мер Первообразная и интеграл
Первообразная и интеграл Комплексные числа
Комплексные числа Параллелепипед. Виды параллелепипедов
Параллелепипед. Виды параллелепипедов Непосредственное интегрирование
Непосредственное интегрирование Понятие производной функции в точке
Понятие производной функции в точке Сравнение чисел
Сравнение чисел Презентация по математике "Умножение двузначного числа на круглое число" - скачать бесплатно
Презентация по математике "Умножение двузначного числа на круглое число" - скачать бесплатно Задачи предельного типа
Задачи предельного типа Способы представления статистических данных
Способы представления статистических данных Построение сечений многогранников
Построение сечений многогранников Несобственные интегралы, зависящие от параметра
Несобственные интегралы, зависящие от параметра Элементы теории множеств
Элементы теории множеств