Операция двоичного сложения и её свойства. Многочлен Жегалкина

Диаграмма Венна для функции «Сложение по модулю 2»

Свойства операции сложение по модулю 2

Свойства операции сложение по модулю 2

Связь между дизъюнкцией
и суммой по

Многочленом Жегалкина называется альтернативная дизъюнкция конъюнкции высказываний, самих высказываний и единицы

Все функции алгебры логики можно выразить через многочленом Жегалкина.

Иван Иванович Жегалкин (1869-1947) – российский и советский математик и

Этих шести формул достаточно, чтобы преобразовывать формулы алгебры логики в многочлен

Пример.

Избавляемся от импликации применяя формулу 4.

Раскрываем скобки и избавляемся от

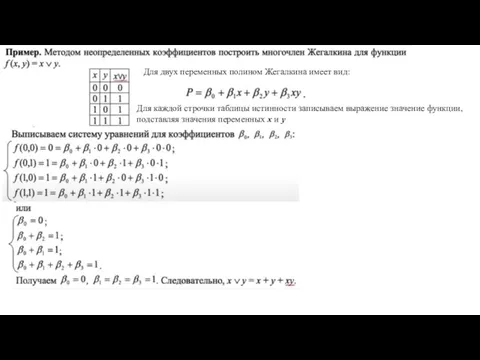
Для каждой строчки таблицы истинности записываем выражение значение функции, подставляя значения

Пример 2. Построить полином Жегалкина для функции
Используя метод неопределённых коэффициентов.

Решение.

Последовательно подставляем наборы значений переменных и находим коэффициенты

Подставляя найденные коэффициенты,

Метод неопределенных коэффициентов (по таблице истинности или вектору значений функции)

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Дополнительное задание.
Пусть функция задана вектором значений
f = (11001011).
Найти