Содержание
- 2. ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ Пермский национальный исследовательский политехнический университет Кафедра математического моделирования систем и процессов
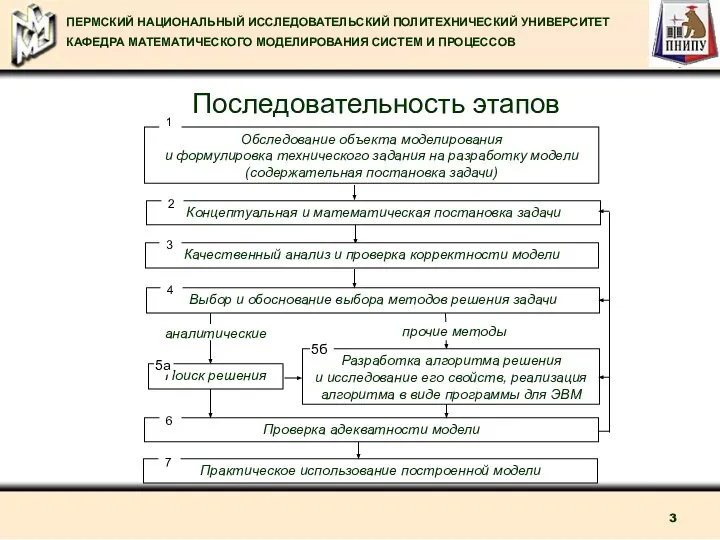
- 3. Последовательность этапов
- 4. 1. Содержательная постановка Заказчик - человек или организация, заинтересованные в создании новой математической модели; Исполнитель -
- 5. 1. Содержательная постановка Этап обследования проводится членами рабочей группы под руководством постановщиков задач и включает следующие
- 6. 1. Содержательная постановка
- 7. 2. Концептуальная постановка задачи Формулируется совокупность гипотез о поведении объекта, его взаимодействии с окружающей средой, изменении
- 8. 2. Математическая постановка задачи Возможные виды задач, появляющиеся при математической постановке: Линейное или нелинейное уравнение; Система
- 9. 2. Математическая постановка задачи Можно выделить несколько наиболее распространенных типов задач, возникающих для систем ОДУ или
- 10. 3. Математическая постановка задачи Проверка корректности математической постановки: Контроль размерностей, включающий правило, согласно которому приравниваться и
- 11. 3. Математическая постановка задачи
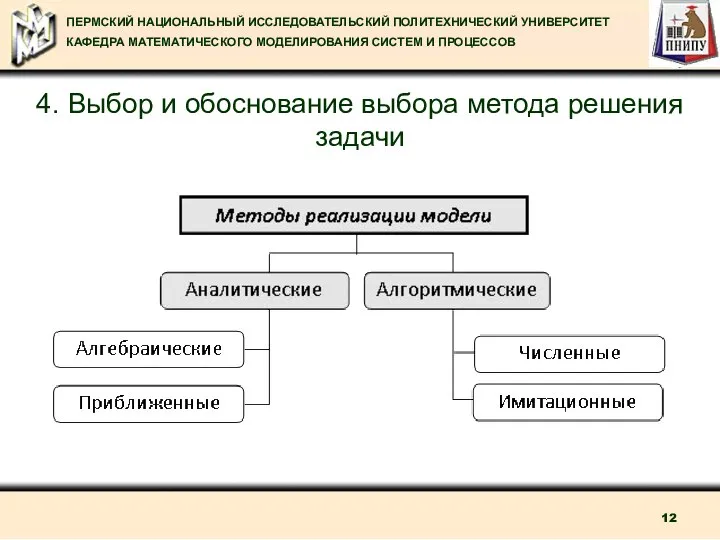
- 12. 4. Выбор и обоснование выбора метода решения задачи
- 13. 4. Выбор и обоснование выбора метода решения задачи Метод реализации модели относят к аналитическим, если он
- 14. 4. Выбор и обоснование выбора метода решения задачи Применение любого численного метода приводит к погрешности результатов
- 15. 4. Выбор и обоснование выбора метода решения задачи Можно выделить следующие группы численных методов по объектам,
- 16. 5. Реализация математической модели в виде программы для ЭВМ Процесс создания программного обеспечения можно разбить на
- 17. Спецификация программы 1) Название задачи Дается краткое определение решаемой задачи, название программного комплекса, указывается система программирования
- 18. Спецификация программы 5) Выходные данные Описываются выходные данные, указывается, в каком виде они должны быть представлены
- 19. 6. Проверка адекватности модели Под адекватностью математической модели будет пониматься степень соответствия результатов, полученных по разработанной
- 20. 6. Проверка адекватности модели Неадекватность результатов моделирования возможна, по крайней мере, по трем причинам: а) Значения
- 21. 7. Практическое использование построенной модели Математические модели могут использоваться: для изучения свойств и особенностей поведения исследуемого
- 22. ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Пермский национальный исследовательский политехнический университет Кафедра математического моделирования систем и процессов
- 23. Пример 1. О баскетболисте Разработать математическую модель, позволяющую описать полет баскетбольного мяча, брошенного игроком в баскетбольную
- 24. Пример 1. О баскетболисте Гипотезы: объектом моделирования является баскетбольный мяч радиуса R; мяч будем считать материальной
- 25. Пример 1. О баскетболисте Математическая постановка: В проекциях на оси координат: Точность броска: Δ = x(tk)
- 27. Скачать презентацию






















 Современные методы обработки статистических данных в области спорта. Корреляция
Современные методы обработки статистических данных в области спорта. Корреляция Наибольший общий делитель и наименьшее общее кратное
Наибольший общий делитель и наименьшее общее кратное Векторы. Понятие вектора
Векторы. Понятие вектора Методы математической статистики в психологопедагогических исследованиях
Методы математической статистики в психологопедагогических исследованиях Игра-зачет Четырехугольники
Игра-зачет Четырехугольники Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Дискретные случайные величины
Дискретные случайные величины Первый признак равенства треугольников
Первый признак равенства треугольников Построение графика квадратичной функции у=ах2+bx+c, a не равно 0
Построение графика квадратичной функции у=ах2+bx+c, a не равно 0 Формулы тригонометрии
Формулы тригонометрии Методы оптимизации
Методы оптимизации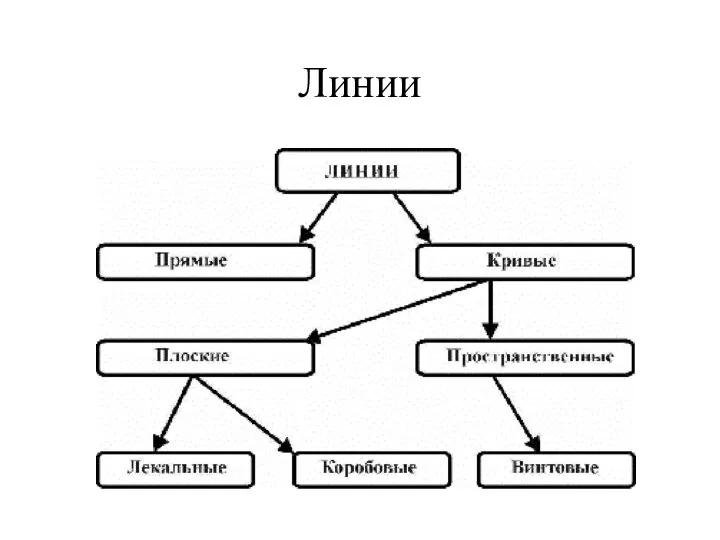 Линии. Плоские кривые. Лекальные кривые
Линии. Плоские кривые. Лекальные кривые Действия с обыкновенными дробями
Действия с обыкновенными дробями Проценты. 5 класс. Урок № 2
Проценты. 5 класс. Урок № 2 Вычисление площадей плоских фигур с помощью определенного интеграла (3)
Вычисление площадей плоских фигур с помощью определенного интеграла (3) Палочки Кюизнера. Мастер-класс. Задание 19 ЕГЭ по математике
Палочки Кюизнера. Мастер-класс. Задание 19 ЕГЭ по математике Смешанные числа
Смешанные числа Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла Аттестационная работа. Образовательная программа элективного курса для 9 класса Решение задач с параметром
Аттестационная работа. Образовательная программа элективного курса для 9 класса Решение задач с параметром Расстояние от точки до прямой. Перпендикулярные прямые
Расстояние от точки до прямой. Перпендикулярные прямые История возникновения дробей
История возникновения дробей Медианы, биссектрисы и высота треугольника
Медианы, биссектрисы и высота треугольника Множества. Основные понятия
Множества. Основные понятия Сложение обыкновенных дробей с одинаковым знаменателем
Сложение обыкновенных дробей с одинаковым знаменателем Среднее арифметическое
Среднее арифметическое Общие темы в математическом искусстве
Общие темы в математическом искусстве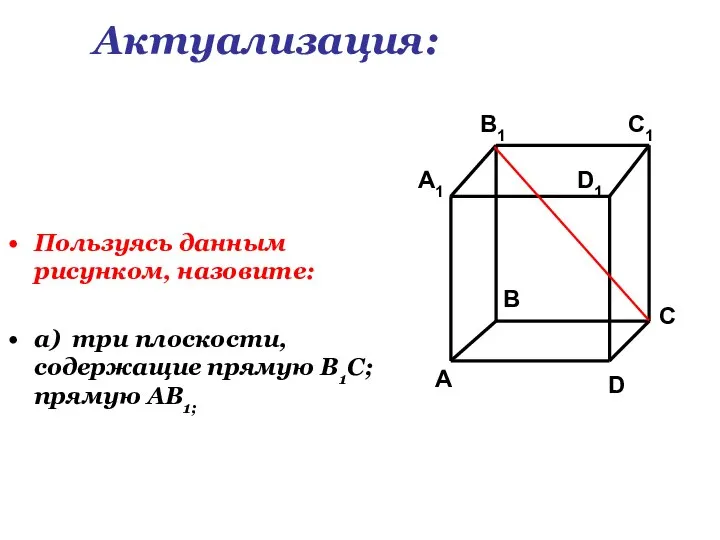 Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую
Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую Решение задач по теме «Векторы». 9 класс
Решение задач по теме «Векторы». 9 класс