Содержание
- 2. 12-ая лекция курса 2021-22: Определения структуры и двух наборов операций, постановка задач Преобразования и Реконструкции. Перевод
- 3. Основные статьи по этим двум Задачам: K.Yu. Gorbunov, V.A. Lyubetsky. Linear time additively exact algorithm for
- 4. Ещё ссылки по задаче преобразования: Горбунов К.Ю., Любецкий В.А. Почти точный линейный алгоритм преобразования графов из
- 5. Определение. Структура a (или b, с, …) – ориентированный граф, состоящий из циклов (включая петли) и
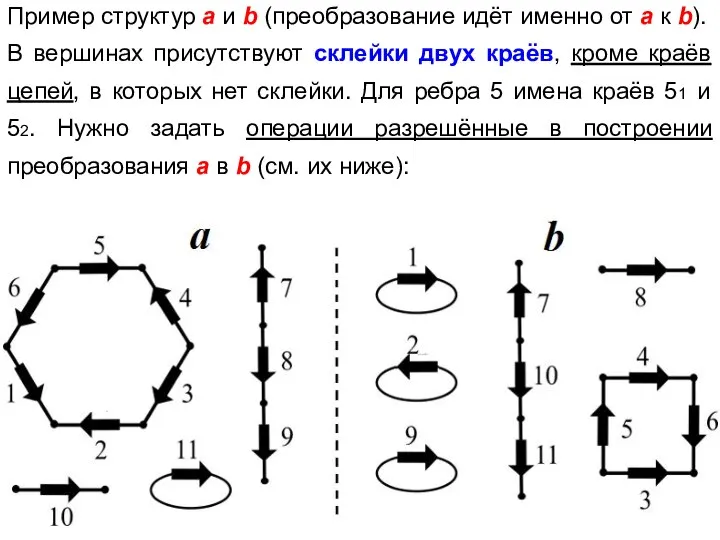
- 6. Пример структур a и b (преобразование идёт именно от a к b). В вершинах присутствуют склейки
- 7. Первый набор операций, SCJ, в Задаче преобразования: расклеить склейку или, обратная операция, склеить два свободных края
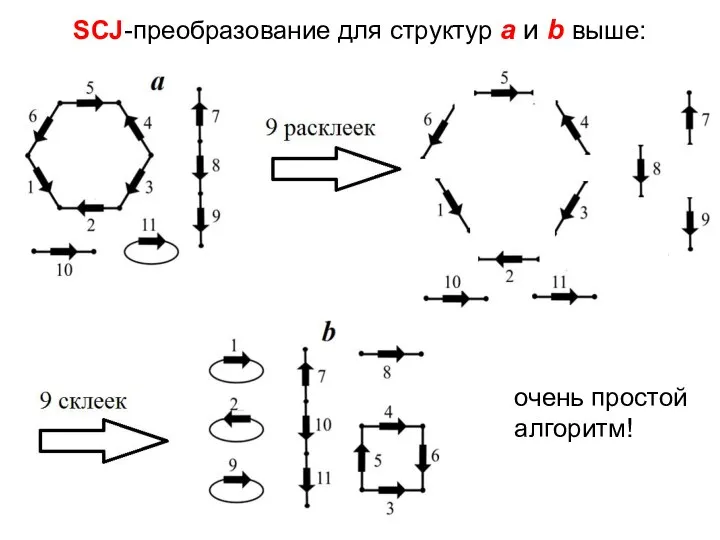
- 8. SCJ-преобразование для структур a и b выше: очень простой алгоритм!
- 9. Алгоритм SCJ-преобразования и SCJ-расстояние : SCJ-кратчайшее преобразование a в b состоит в расклейке всех склеек в
- 10. Структуры a в b называются с равным составом, если множества их имён (=их рёбер с их
- 11. Второй набор операций, DCJ, в Задаче преобразования: расклеить две склейки и склеить четыре образовавшиеся свободных (т.е.
- 12. Итак, 4 операции (будут ещё две): расклеить какую-либо вершину (Cut), как было; склеить два свободных (т.е.
- 13. К этим четырём операциям добавляются ещё две операции: удалить (Rem) связный участок рёбер с именами из
- 14. Примеры этих операций над структурой a, которые цепочкой преобразуют a в b: 1) удалить связный (не
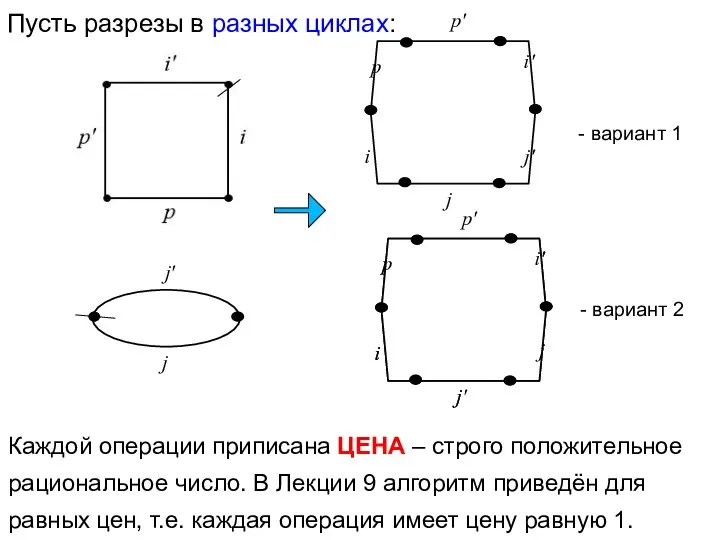
- 15. Каждой операции приписана ЦЕНА – строго положительное рациональное число. В Лекции 9 алгоритм приведён для равных
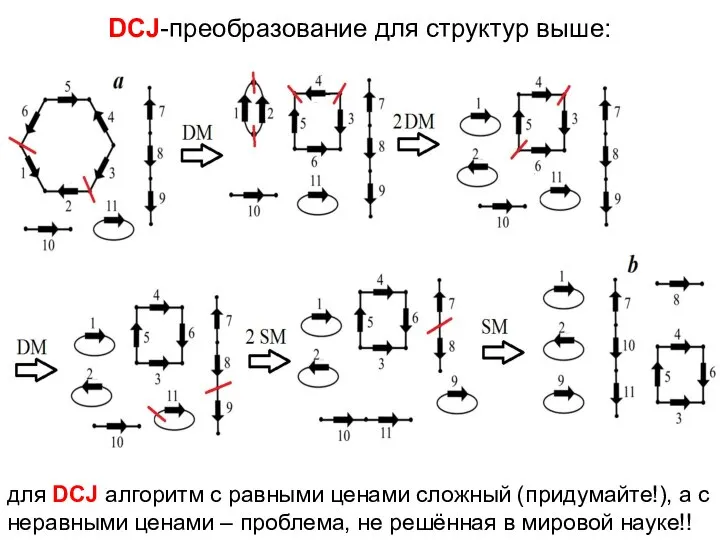
- 16. DCJ-преобразование для структур выше: для DCJ алгоритм с равными ценами сложный (придумайте!), а с неравными ценами
- 17. Понятие дерева с данными в листьях:
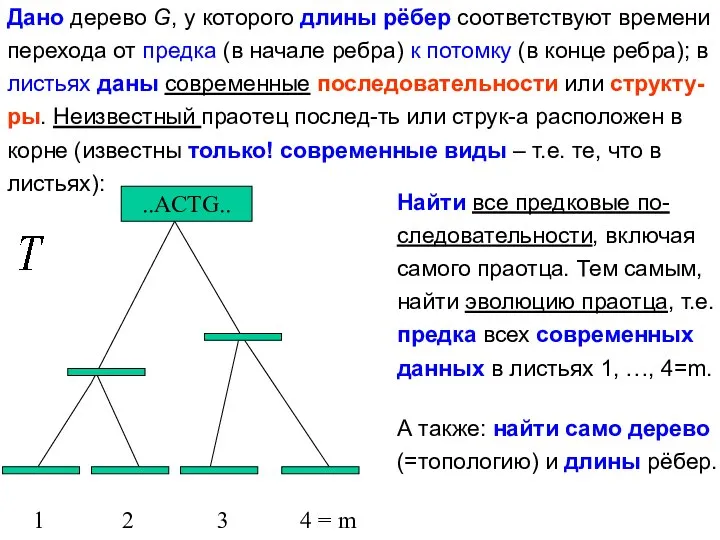
- 18. Дано дерево G, у которого длины рёбер соответствуют времени перехода от предка (в начале ребра) к
- 19. Мы рассматриваем деревья с корнем. При наличии корня подразумевается ориентация рёбер: на каждом ребре задаётся направление
- 20. Приведём всё это как Математические определения. Неукоренённое дерево – связный ациклический граф любые две вершины
- 21. Теория ЭВОЛЮЦИИ ( ФИЛОГЕНЕТИКА) – это: происхождение и развитие Живого в физическом или дискретном времени, его
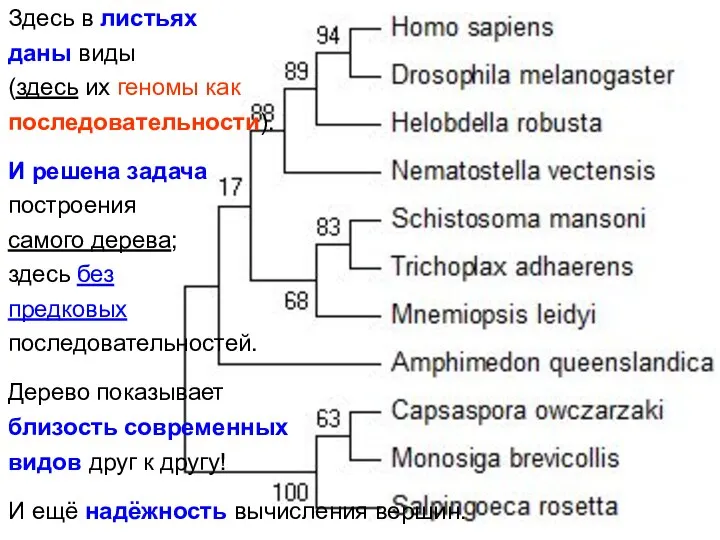
- 22. Здесь в листьях даны виды (здесь их геномы как последовательности). И решена задача построения самого дерева;
- 23. задача РЕКОНСТРУКЦИИ – продолжить последовательности или структуры, заданные в листьях данного дерева, на его внутренние вершины
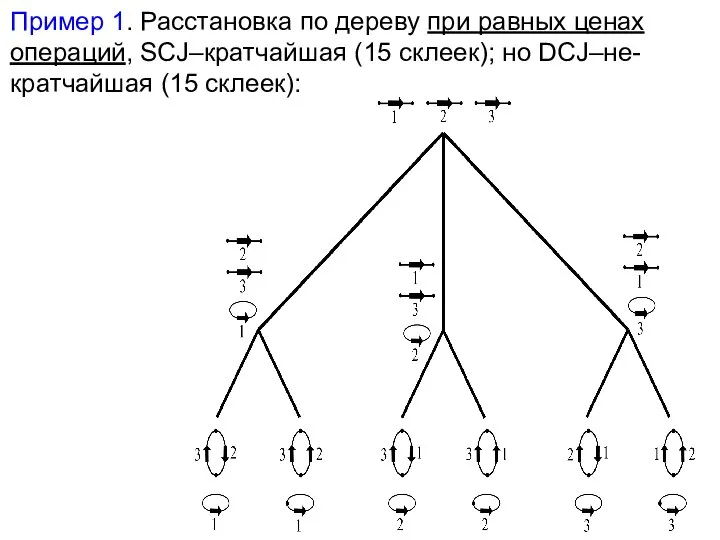
- 24. Пример 1. Расстановка по дереву при равных ценах операций, SCJ–кратчайшая (15 склеек); но DCJ–не-кратчайшая (15 склеек):
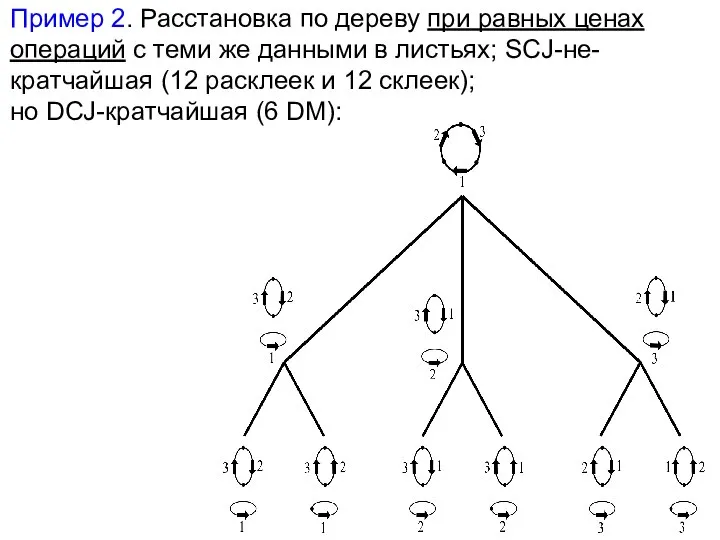
- 25. Пример 2. Расстановка по дереву при равных ценах операций с теми же данными в листьях; SCJ-не-кратчайшая
- 26. Варианты постановки задачи Реконструкции: в листовых структурах разрешены повторения имён (= т.е. там возможны паралоги) или
- 27. Итак, даны дерево и в каждом его листе структура. (Удобно считать, что она беспетлевая ,т.е. не
- 28. Переход к равенству составов в листьях выполняется так: в каждый лист (=в структуру листа) добавим k-петлю
- 29. Для данной структуры a обозначим М множество краёв рёбер из a, т.е. М состоит из имён
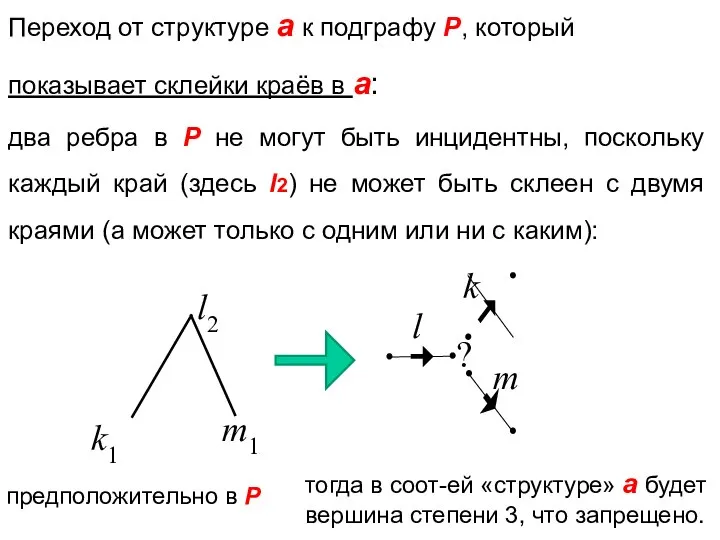
- 30. k1 Переход от структуре a к подграфу Р, который показывает склейки краёв в a: два ребра
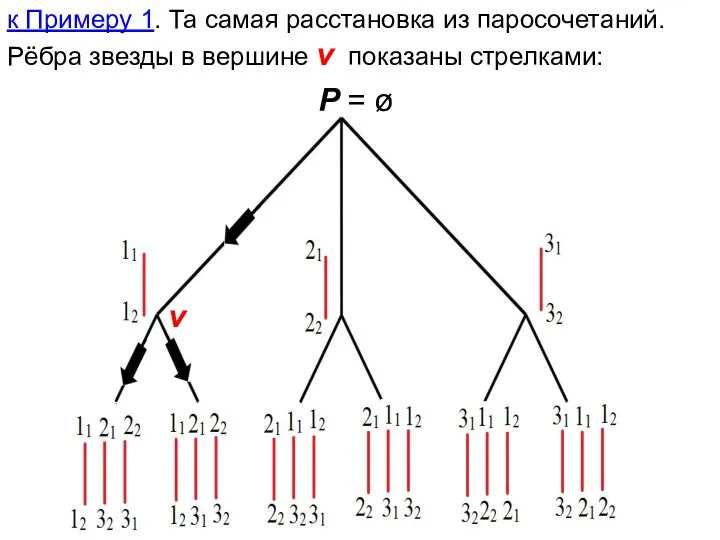
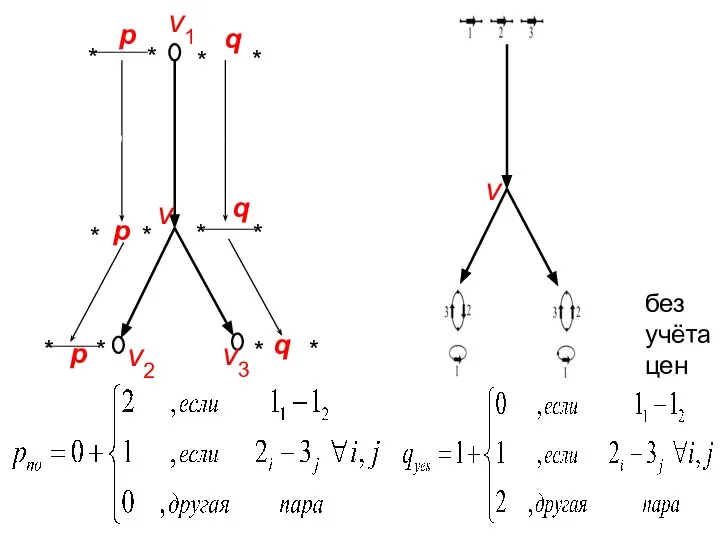
- 31. к Примеру 1. Та самая расстановка из паросочетаний. Рёбра звезды в вершине v показаны стрелками: P
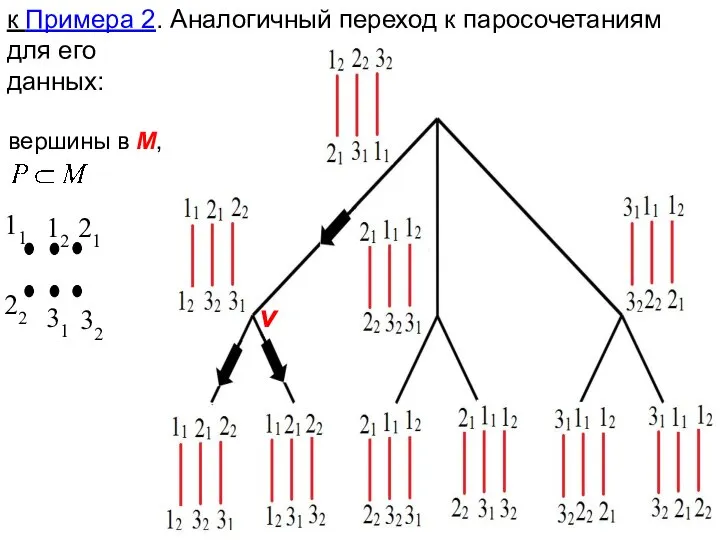
- 32. к Примера 2. Аналогичный переход к паросочетаниям для его данных: v 11 22 вершины в М,
- 33. Локально минимальной назовём расстановку по дереву, для которой в любой одной вершине замена структуры на любую
- 34. Итак, дан неориентированный без петель полный граф М, в нём каждому ребру в дальнейшем приписано натуральное
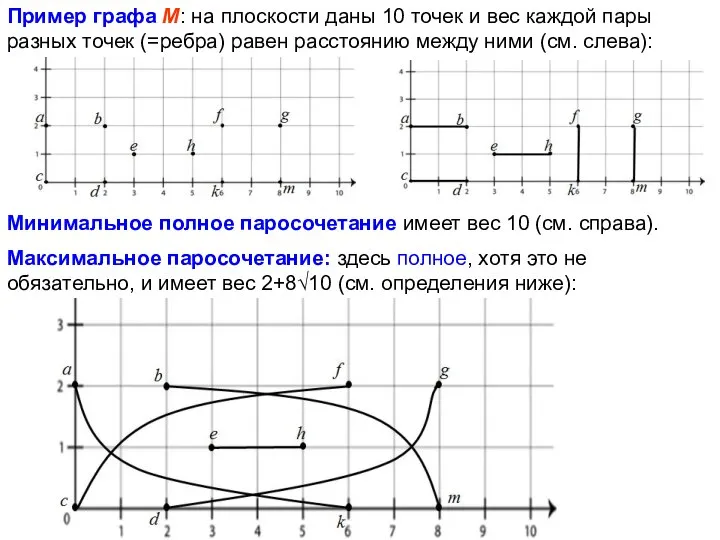
- 35. Пример графа М: на плоскости даны 10 точек и вес каждой пары разных точек (=ребра) равен
- 36. Минимальным называется полное паросочетание, на котором достигает минимума сумма длин его рёбер. Минимальное (автоматически: полное) паросочетание
- 37. Даны дерево Т и расстановка по Т. Звездой называется подграф, состоящий из какой-то вершины v в
- 38. без учёта цен
- 39. Пусть p пара разных краёв (=ребро) в Мv (см. сл. 31-32): в предположении p не склеена
- 40. Задача. Для примеров 1-2 и звезд в в них вычислите значения pno и pyes (все без
- 41. Лемма 1. Для звезды в v (как отдельного дерева Т) S равна где = суммарная цена
- 42. Алгоритм для звезды в v : Припишем каждому ребру q в Мv вес , и ищем
- 43. Итак, наша задача: найти низкой сложности алгоритм, который строит локально минимальную расстановку – по дереву и
- 44. Иначе среди всех вершин найдём v1 с наибольшим (v1). В v1 подставим максимальное паросочетание P1 для
- 45. Каждой (неупорядоченной) паре p различных краёв рёб-ер в вершине v исходного дерева сопоставим вероятно-сть xvp :
- 47. Скачать презентацию































 Формулы сокращенного умножения. (Найди ошибку) 7 класс
Формулы сокращенного умножения. (Найди ошибку) 7 класс Параболалық теңдеуге қойылған бастапқы-шеттік есепті Галеркин әдісімен шешу
Параболалық теңдеуге қойылған бастапқы-шеттік есепті Галеркин әдісімен шешу Решение комбинаторных задач (2)
Решение комбинаторных задач (2) Анализ качественных переменных
Анализ качественных переменных Как люди научились считать Выполнили учащиеся 5 класса. Руководитель: учитель математики Худакова Г.Н.
Как люди научились считать Выполнили учащиеся 5 класса. Руководитель: учитель математики Худакова Г.Н.  Геометрическая вероятность
Геометрическая вероятность Презентация по математике "Математику уже затем учить надо, что она ум в порядок приводит" - скачать
Презентация по математике "Математику уже затем учить надо, что она ум в порядок приводит" - скачать  Вводное повторение.Геометрия 8 класс
Вводное повторение.Геометрия 8 класс Ряды. Лекция
Ряды. Лекция Повторение (1 урок алгебра) 7 класс
Повторение (1 урок алгебра) 7 класс Типы случайных событий и действия над ними. Теория вероятностей
Типы случайных событий и действия над ними. Теория вероятностей Система задач на тему двугранный угол
Система задач на тему двугранный угол Жінки-математики
Жінки-математики Математические основы компьютерной графики. Лекция 2
Математические основы компьютерной графики. Лекция 2 Разнообразные подходы к решению текстовых задач
Разнообразные подходы к решению текстовых задач Прямоугольный треугольник
Прямоугольный треугольник МПМ-матрица посадочных лист
МПМ-матрица посадочных лист Функция у=ах²+вх+с
Функция у=ах²+вх+с Презентация на тему число 8
Презентация на тему число 8 Первый и второй замечательные пределы и способы их вычисления. (Семинар 6)
Первый и второй замечательные пределы и способы их вычисления. (Семинар 6) Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Признаки делимости. 5 класс
Признаки делимости. 5 класс Осевая и центральная симметрии
Осевая и центральная симметрии Применение средств ЭВМ при обработке данных активного эксперимента
Применение средств ЭВМ при обработке данных активного эксперимента Презентация на тему Задачи на взвешивание
Презентация на тему Задачи на взвешивание Упращение выражений
Упращение выражений Математика в мире животных
Математика в мире животных Результаты изучения квадратичной функции в основной и старшей школе
Результаты изучения квадратичной функции в основной и старшей школе