Содержание
- 2. ДЛЯ ЧЕГО БЫЛИ ПРИДУМАНЫ ЛОГАРИФМЫ ? КАК СКАЗАЛ ФРАНЦУЗСКИЙ МАТЕМАТИК П. ЛАПЛАС, «ИЗОБРЕТЕНИЕ ЛОГАРИФМОВ, СОКРАТИВ РАБОТУ
- 3. ДЛЯ ЧЕГО БЫЛИ ПРИДУМАНЫ ЛОГАРИФМЫ ? …Если необходимость совершать обратную операцию к операции возведения в n-ую
- 4. Джон Непер (1550-1617) – английский математик. Изобретатель логарифмов, составитель первой таблицы логарифмов, облегчавшей работу вычислителей многих
- 5. Решите уравнения: x = 3 x = ? ?
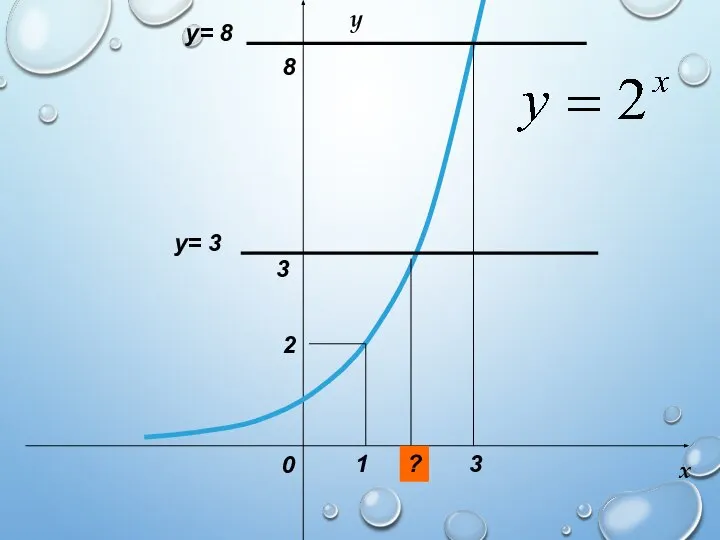
- 6. 0 3 8 3 y= 3 1 2 y= 8 x y ?
- 7. Решите уравнения: x = 3 ?
- 8. ВОЗВЕДЕНИЕ В СТЕПЕНЬ ИМЕЕТ ДВА ОБРАТНЫХ ДЕЙСТВИЯ ОТЫСКАНИЕ A – ИЗВЛЕЧЕНИЕ КОРНЯ; НАХОЖДЕНИЕ В – ЛОГАРИФМИРОВАНИЕ.
- 9. ОПРЕДЕЛЕНИЕ ЛОГАРИФМОМ ПОЛОЖИТЕЛЬНОГО ЧИСЛА В ПО ОСНОВАНИЮ А, ГДЕ А>0,A=1,НАЗЫВАЕТСЯ ПОКАЗАТЕЛЬ СТЕПЕНИ, В КОТОРУЮ НУЖНО ВОЗВЕСТИ
- 10. ВСПОМНИТЕ УРАВНЕНИЕ ИЗ ПЕРВОГО СЛАЙДА: МЫ ГОВОРИЛИ, ЧТО НАХОЖДЕНИЕ B – ЛОГАРИФМИРОВАНИЕ. МАТЕМАТИКИ ДОГОВОРИЛИСЬ ЗАПИСЫВАТЬ ЭТО
- 11. НАПРИМЕР: так как так как так как так как
- 12. НАЙТИ ЗНАЧЕНИЕ ЛОГАРИФМОВ:
- 13. НАЙТИ ЗНАЧЕНИЕ ЛОГАРИФМОВ:
- 14. Не имеет смысла НАЙТИ ЗНАЧЕНИЕ ЛОГАРИФМОВ:
- 15. Определение логарифма можно записать так: a log a b = b Это равенство справедливо при b>0,
- 16. Log 2 16; log 2 64; log 2 2; Log 2 1 ; log 2 (1/2);
- 17. Сравните со своими ответами ! Log 2 16; log 2 64; log 2 2; Log 2
- 19. Скачать презентацию







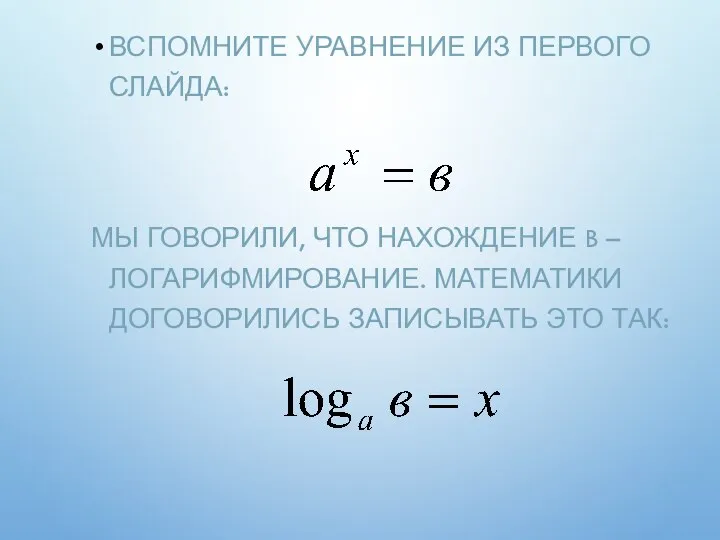







 Основы маневрирования. Тема 12
Основы маневрирования. Тема 12 Градиентные методы решения ЗНЛП
Градиентные методы решения ЗНЛП Куб та його властивості
Куб та його властивості Непрерывность функции
Непрерывность функции Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Probabilities. Week 5 (2)
Probabilities. Week 5 (2) Все о треугольниках
Все о треугольниках Взаимно простые числа. Признак делимости
Взаимно простые числа. Признак делимости Алгоритм принятия решения о выборе критерия оценки измерений
Алгоритм принятия решения о выборе критерия оценки измерений Нахождение корней уравнения методом деления отрезка пополам
Нахождение корней уравнения методом деления отрезка пополам Машинная арифметика в рациональных числах (лекция 8)
Машинная арифметика в рациональных числах (лекция 8) Делители и кратные
Делители и кратные Теорема Чевы
Теорема Чевы Моделирование многогранников. Правильные многогранники
Моделирование многогранников. Правильные многогранники Тренировочная работа № 30
Тренировочная работа № 30 Уравнения-следствия
Уравнения-следствия Алгебра логики. Понятие высказывания
Алгебра логики. Понятие высказывания Математический диктант. Решите уравнения
Математический диктант. Решите уравнения Научный проект по математике
Научный проект по математике Цилиндр. История возникновения
Цилиндр. История возникновения Рационал сандарды қорытындылау
Рационал сандарды қорытындылау Целые и рациональные числа. Действительные числа
Целые и рациональные числа. Действительные числа Принцип неопределенности Гейзенберга
Принцип неопределенности Гейзенберга Погрешность и точность приближения. Абсолютная и относительная погрешности
Погрешность и точность приближения. Абсолютная и относительная погрешности Отношения между понятиями 6 класс
Отношения между понятиями 6 класс  Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии урок алгебры в 8 классе
урок алгебры в 8 классе  Число и цифра 2
Число и цифра 2