Содержание
- 2. 1. МНОЖЕСТВА 1.1. ПОНЯТИЕ МНОЖЕСТВА. ЛОГИЧЕСКИЕ СИМВОЛЫ.
- 3. Логические символы. ∈- знак принадлежности ∀- квантор всеобщности ∃- квантор существования ⇒- знак логического следования ⇔-
- 4. Множества. Способы задания. {a} - одноэлементное множество; ∅- пустое множество Действительные корни уравнения ∃ множества конечные
- 5. Отношения между множествами. Определение 1.1. Множества A и B называются равными, если каждый элемент множества A
- 6. Пример:
- 7. Свойства равенства: A=A (рефлексивность); A=B, B=C ⇒ A=C (транзитивность); A=B ⇒ B=A (симметричность). Неравенство множеств обозначают
- 8. Определение 1.2. Множество A (A ≠ ∅) называется подмножеством множества B (B ≠ ∅), если каждый
- 9. 1.2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ. V – основное или универсальное множество. 1) В планиметрии V = 2)
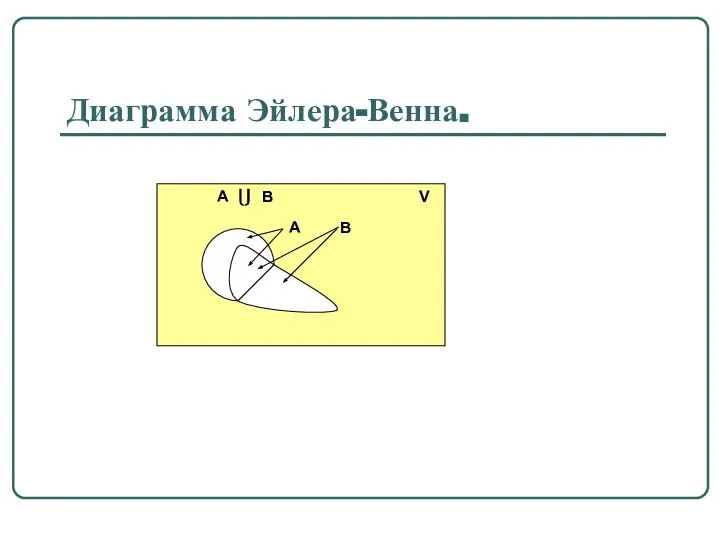
- 10. Диаграмма Эйлера-Венна.
- 11. Свойства объединения множеств. 1) A ⎩⎭ B = B ⎩⎭ A (коммутативность), 2) A ⎩⎭ (
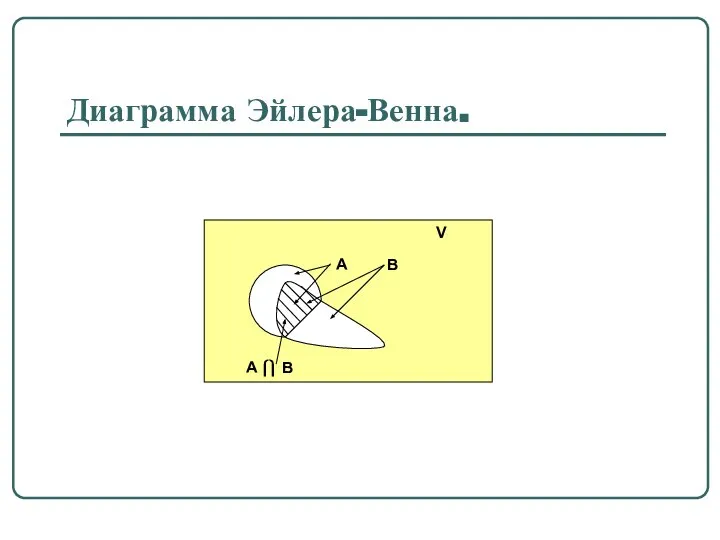
- 12. Определение 1.4. Пересечением множеств A и B называется множество A ⎧⎫ B, состоящее из всех тех
- 13. Диаграмма Эйлера-Венна.
- 14. Свойства пересечения множеств. 1) A ⎧⎫ B = B ⎧⎫ A (коммутативность), 2) A ⎧⎫ (
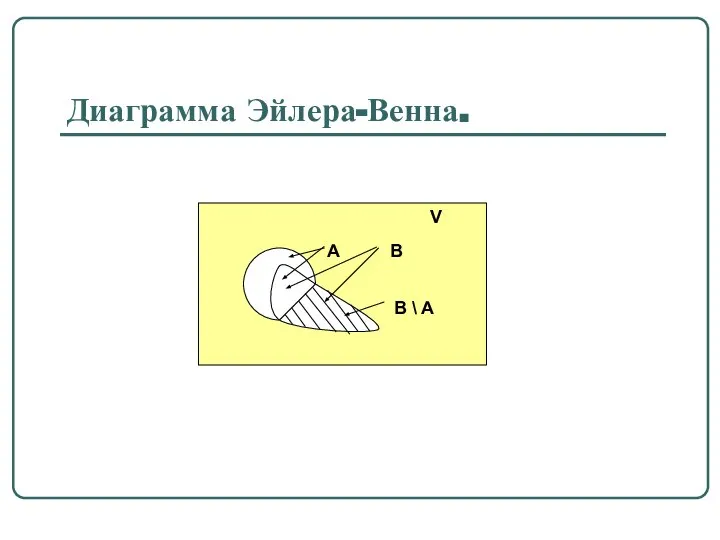
- 15. Определение 1.5. Разностью двух множеств B и A называется множество B \ A, состоящее из всех
- 16. Диаграмма Эйлера-Венна.
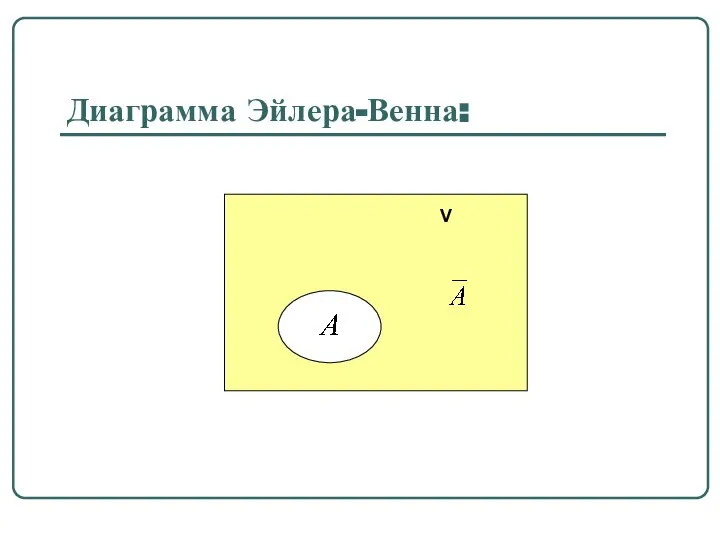
- 17. Определение 1.6. Разность V \ A называется дополнением множества A до универсального множества V и обозначается
- 18. Диаграмма Эйлера-Венна:
- 19. Пара элементов ( x ; y ), x ∈ A, y ∈ B называется упорядоченной, если
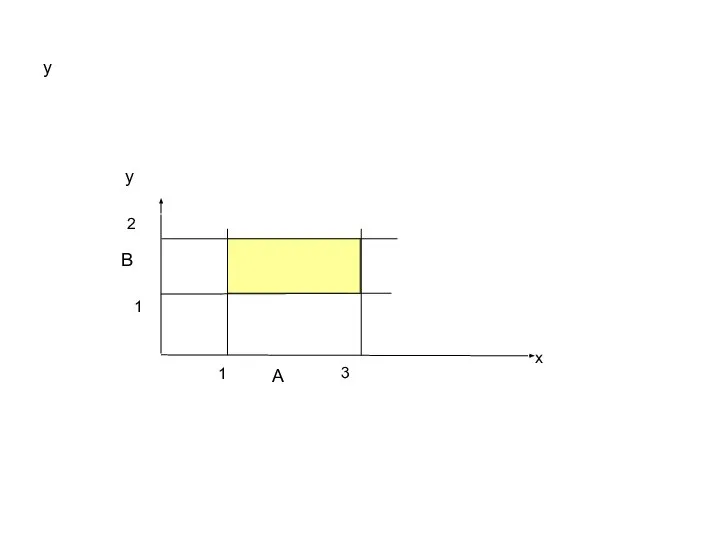
- 20. Определение 1.7. Декартовым произведением двух множеств A и B называется множество, обозначаемое A × B, состоящее
- 21. y
- 22. 1.3. ОТОБРАЖЕНИЕ МНОЖЕСТВ. ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ. Пусть A и B - произвольные множества. Пусть f - закон
- 23. Определение отображения: f : A → B ⇔ ∀ a ∈ A ∃ b ∈ B
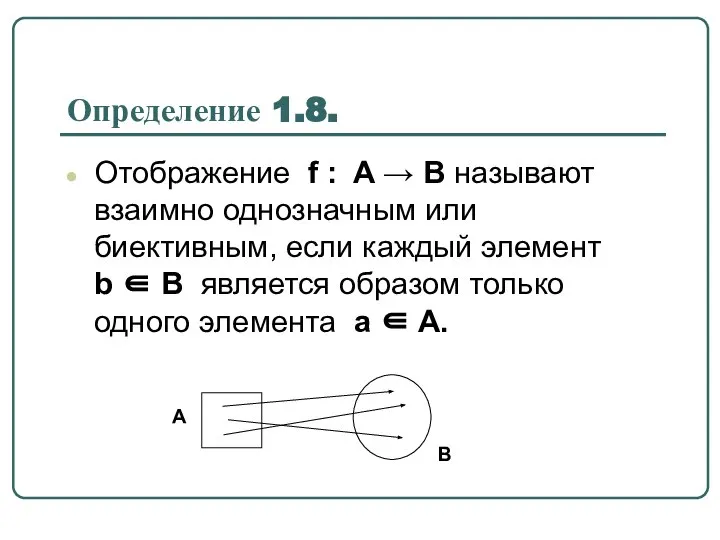
- 24. Определение 1.8. Отображение f : A → B называют взаимно однозначным или биективным, если каждый элемент
- 25. ЛЕКЦИЯ 2 2. ЧИСЛОВЫЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ.
- 26. f – взаимно однозначное отображение ⇔ ∀ b ∈ B ∃ a ∈ A : b
- 27. Пример:
- 28. Определение 1.10. Два множества A и B называются эквивалентными (равномощными), если ∃ хотя бы одно взаимно
- 29. 1.4. ЧИСЛОВЫЕ МНОЖЕСТВА. Множество натуральных чисел N. N = {1, 2, 3, …}. Свойства: 1) выполняются:
- 30. Множество целых чисел Z. Z = { …, -2, -1, 0, 1, 2, …}. Свойства: Определены
- 31. Множество рациональных чисел Q. Q = { q = p / n | p ∈ Z
- 32. Множество действительных чисел R. Свойства: R – упорядоченно; R –бесконечно; N ⊂ Z ⊂ Q ⊂
- 33. 2.1 ПОНЯТИЕ ФУНКЦИИ. СПОСОБЫ ЗАДАНИЯ. Пусть D – произвольное подмножество действительных чисел (D⊆R). Если каждому числу
- 34. Термины функция, отображение, преобразование – синонимы. Обозначения: y=f(x); f: D→E; В данной главе рассматриваются функции одной
- 35. Аналитический способ задания функций. С помощью формул Частное значение функции: Область определения либо указывают D(f)=[1;2], либо
- 36. Пример:
- 37. Составные функции:
- 38. Неявно заданные функции: F(x,y)=0 Если уравнение можно разрешить относительно y, то приходим к явно заданной функции.
- 39. Табличный способ задания функций. Примеры: таблицы ln, sin и т. д. + Точное значение при .
- 40. Графический способ задания функций.
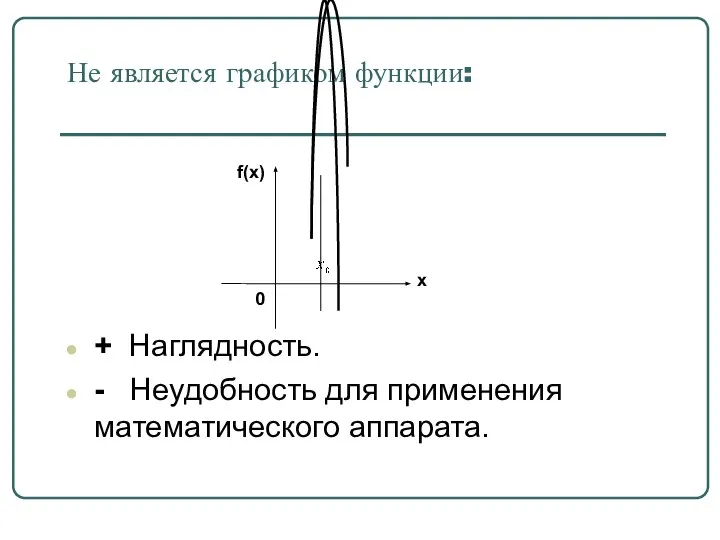
- 41. Не является графиком функции: + Наглядность. - Неудобность для применения математического аппарата.
- 42. 2.2 ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПОВЕДЕНИЯ ФУНКЦИЙ. Начальный этап исследования функции. 1) Нули f(x)=0 и знак функции на
- 43. 4) Монотонность: монотонно возрастающая, если монотонно убывающая, если 5) Ограниченность: ограниченная сверху ⇔ ∃ M∈R: ∀
- 44. 2.3 СЛОЖНАЯ ФУНКЦИЯ. ОБРАТНАЯ ФУНКЦИЯ. Сложная функция. На D определена функция u=ϕ(x) → E(u) – множество
- 45. Обратная функция. Функция y=f(x) отображает D(f) → E(f). Рассмотрим взаимно однозначное отображение Тогда можно говорить об
- 46. Теорема 2.1. Если числовая функция монотонна, то ∃ обратная функция Это достаточное условие обратимости.
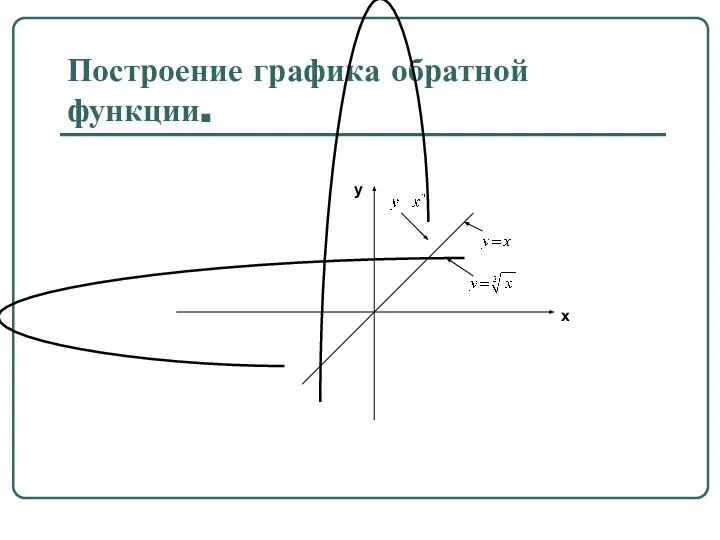
- 47. Построение графика обратной функции.
- 48. 2.4. ОСНОВНЫЕ ЧИСЛОВЫЕ ФУНКЦИИ И ИХ ГРАФИКИ. 1) Линейная: y=ax+b (a,b∈R), D(f)=R.
- 49. 2) Квадратичная функция.
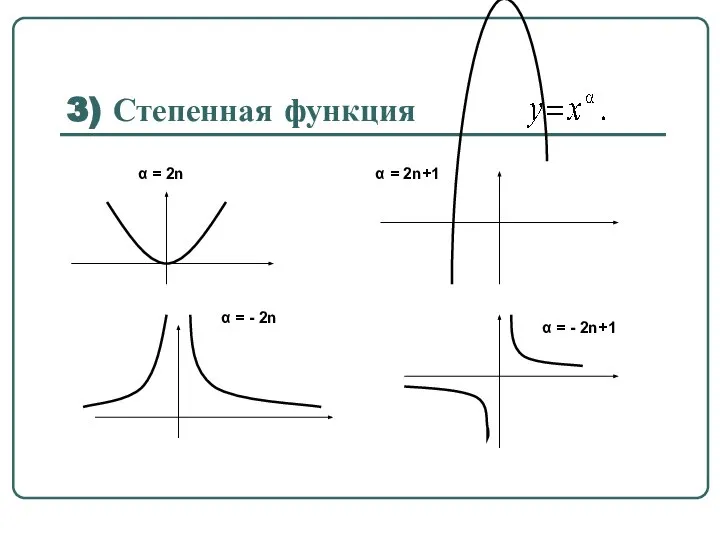
- 50. 3) Степенная функция
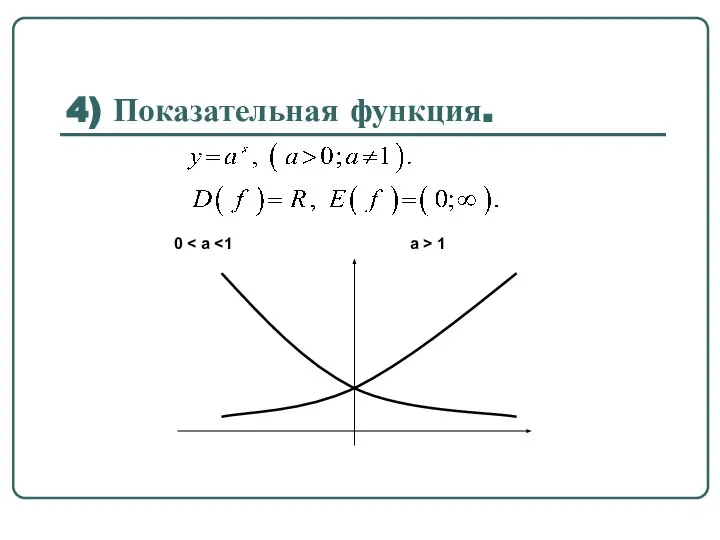
- 51. 4) Показательная функция.
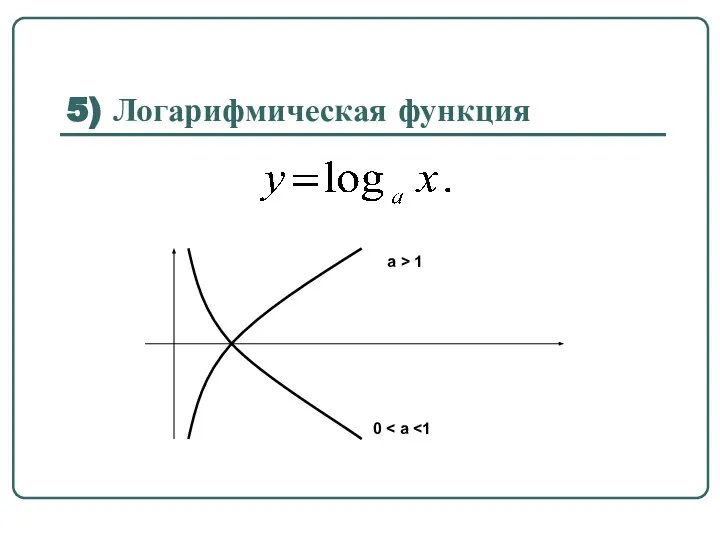
- 52. 5) Логарифмическая функция
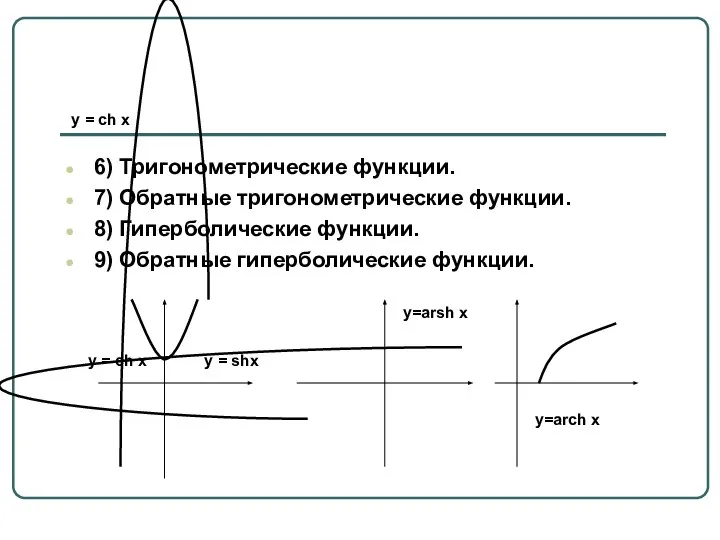
- 53. y = ch x 6) Тригонометрические функции. 7) Обратные тригонометрические функции. 8) Гиперболические функции. 9) Обратные
- 54. ЛЕКЦИЯ 3 2. ЧИСЛОВЫЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ.
- 55. 2.5. КЛАССИФИКАЦИЯ ФУНКЦИЙ. 1) Целые рациональные функции: 2) Дробно-рациональные функции: Совокупность 1) и 2) – класс
- 56. 2.6. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ. t – называется параметром. Если ϕ - монотонна, то ∃ Тогда Всякую
- 57. Пример: а) Введем Тогда б) а) Введем Тогда
- 58. Параметрическое задание линий на плоскости. Множество точек M(x,y) плоскости координаты которых удовлетворяют x=x(t), y=y(t), t∈T, параметрически
- 59. Окружность с центром в начале координат.
- 60. Парабола. Гипербола.
- 61. Астроида.
- 63. Скачать презентацию
















































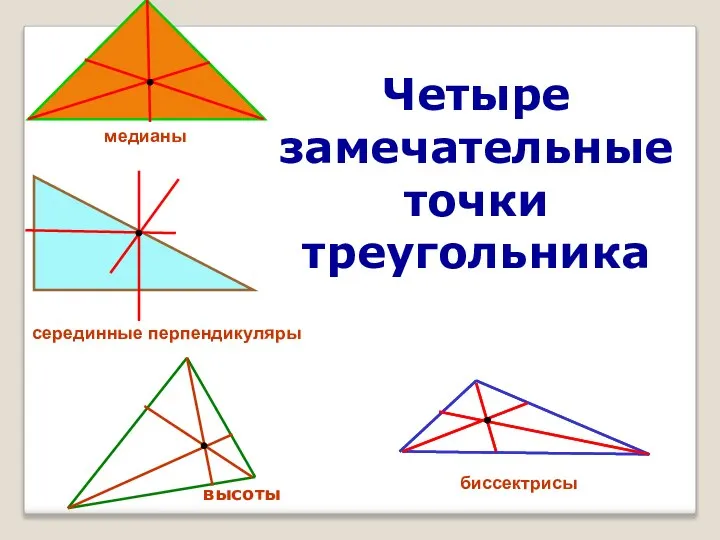 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Признаки делимости
Признаки делимости Интерактивный тест по математике. Решаем задачи с Буратино (3 класс)
Интерактивный тест по математике. Решаем задачи с Буратино (3 класс) Decision trees. Деревья решений
Decision trees. Деревья решений Геометрия 7 класс Основные темы
Геометрия 7 класс Основные темы Работу выполнила Артамонова Лариса Владимировна - учитель математики первой квалификационной категории, МОУ «Москаленский
Работу выполнила Артамонова Лариса Владимировна - учитель математики первой квалификационной категории, МОУ «Москаленский  Первый признак подобия треугольников, применение его при решении задач
Первый признак подобия треугольников, применение его при решении задач Интерактивный тренажёр Осенний. Математика 1 класс. Сложение и вычитание в пределах 5
Интерактивный тренажёр Осенний. Математика 1 класс. Сложение и вычитание в пределах 5 Арифметический диктант
Арифметический диктант Методы геометрии
Методы геометрии Глубина озера. Теорема Пифагора
Глубина озера. Теорема Пифагора Точность и качество измерений: понятия погрешности, точности, достоверности, сходимости, правильности
Точность и качество измерений: понятия погрешности, точности, достоверности, сходимости, правильности Инфиксная. Постфиксная. Префиксная
Инфиксная. Постфиксная. Префиксная Задания по математике. (Вариант 7)
Задания по математике. (Вариант 7) Измерение отрезков и углов
Измерение отрезков и углов Главные направления линии второго порядка
Главные направления линии второго порядка Степень с целым показателем и ее свойства
Степень с целым показателем и ее свойства 1 признак подобия треугольников
1 признак подобия треугольников Артамонова Л.В. Учитель математики МКОУ «Москаленский лицей»
Артамонова Л.В. Учитель математики МКОУ «Москаленский лицей» Линейные ДУ
Линейные ДУ Презентация по математике "Загадочное число П" - скачать бесплатно
Презентация по математике "Загадочное число П" - скачать бесплатно Производная. Тест по алгебре
Производная. Тест по алгебре Понятие одночлена. Стандартный вид одночлена
Понятие одночлена. Стандартный вид одночлена Задача дробово-лінійного програмування. Методи оптимізації та дослідження операцій. (Лекция 5)
Задача дробово-лінійного програмування. Методи оптимізації та дослідження операцій. (Лекция 5) Сходимость знакопеременных рядов
Сходимость знакопеременных рядов Прямое сложение и вычитание
Прямое сложение и вычитание История числа Пи
История числа Пи Теория оптимизации
Теория оптимизации