Содержание
- 2. Определение Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники, и в каждой вершине
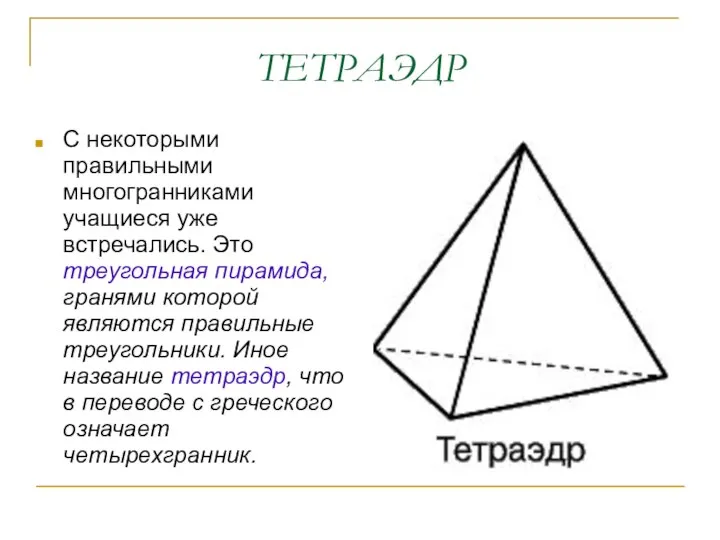
- 3. ТЕТРАЭДР С некоторыми правильными многогранниками учащиеся уже встречались. Это треугольная пирамида, гранями которой являются правильные треугольники.
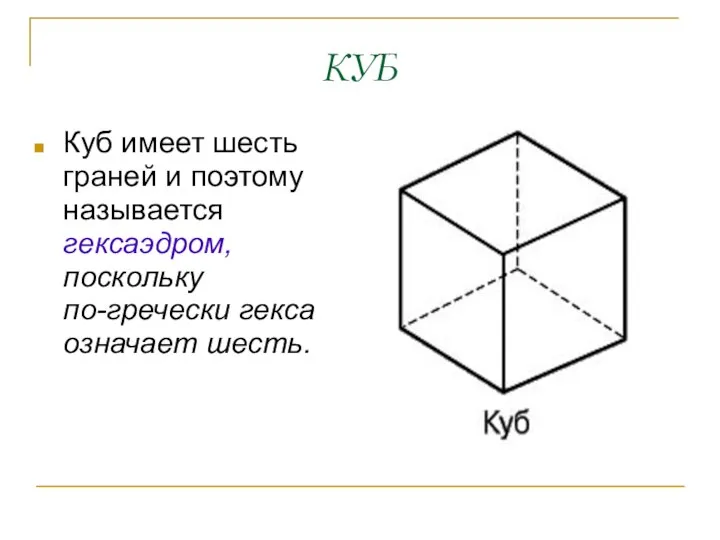
- 4. КУБ Куб имеет шесть граней и поэтому называется гексаэдром, поскольку по-гречески гекса означает шесть. Добавьте графияческий
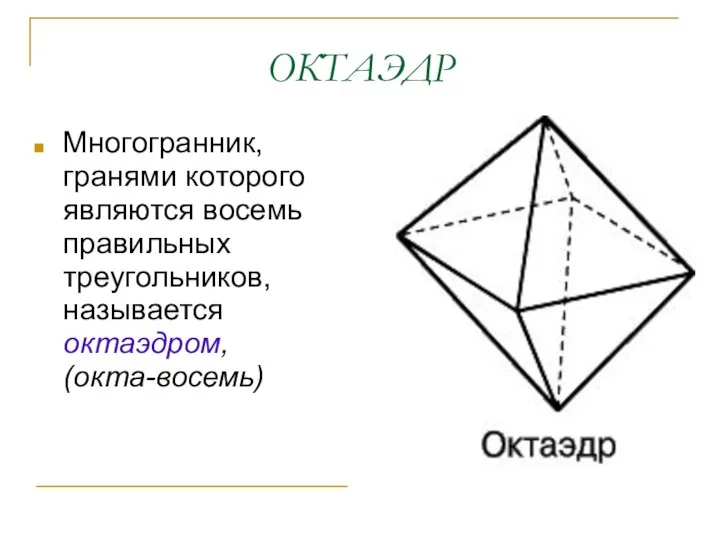
- 5. ОКТАЭДР Многогранник, гранями которого являются восемь правильных треугольников, называется октаэдром, (окта-восемь)
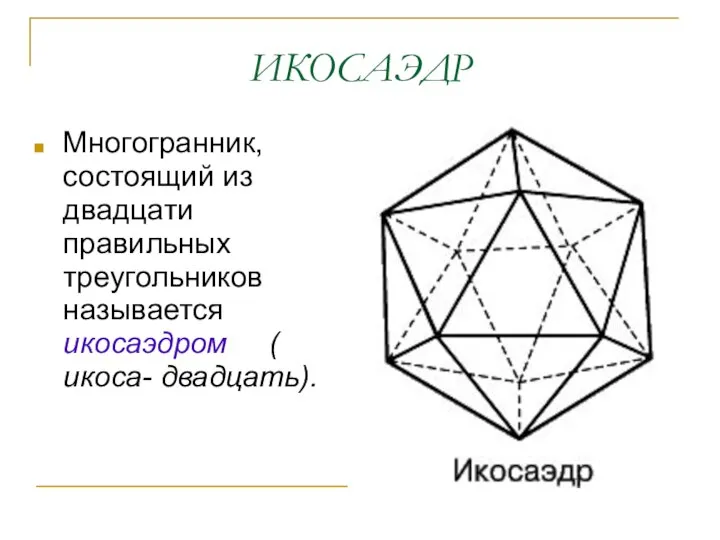
- 6. ИКОСАЭДР Многогранник, состоящий из двадцати правильных треугольников называется икосаэдром ( икоса- двадцать).
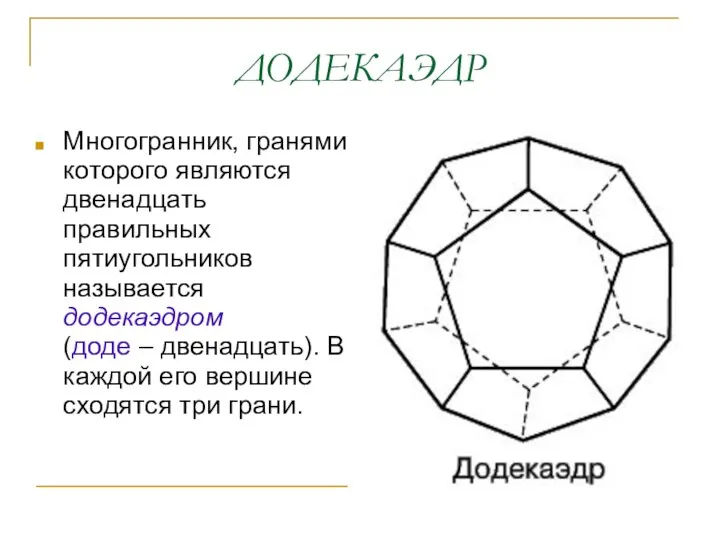
- 7. ДОДЕКАЭДР Многогранник, гранями которого являются двенадцать правильных пятиугольников называется додекаэдром (доде – двенадцать). В каждой его
- 8. ПРИМЕЧАНИЕ В вершинах выпуклого многогранника не могут сходиться правильные многоугольники, у которых число сторон больше пяти,
- 9. ЗАДАЧИ Почему гранями правильного многогранника не могут быть правильные шестиугольники? Представьте многогранник – бипирамиду, сложенную из
- 10. ЗАДАЧИ Нарисуйте правильные многогранники. Покажите, что центры граней куба являются вершинами октаэдра и, наоборот, центры граней
- 11. ЗАДАЧИ Ребро октаэдра равно а. Определите расстояние между его противоположными вершинами (ось октаэдра). Ребро куба равно
- 12. ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ Полуправильным называется выпуклый многогранник, гранями которого являются правильные многоугольники( возможно и с разным числом
- 13. ПРИЗМА К полуправильным многогранникам относятся правильные n-угольные призмы, все ребра которых равны. Например правильная шестиугольная призма
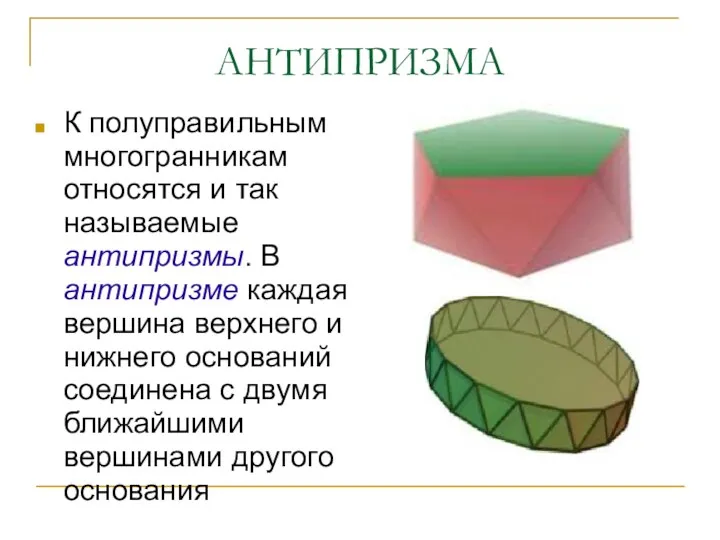
- 14. АНТИПРИЗМА К полуправильным многогранникам относятся и так называемые антипризмы. В антипризме каждая вершина верхнего и нижнего
- 15. Тела Архимеда Кроме бесконечных серий призм и антипризм имеется еще только 14 полуправильных многогранников, 13 из
- 16. «УСЕЧЕНИЯ» Самые простые из них получаются из правильных многогранников операцией «усечения», состоящей в отсечении плоскостями углов
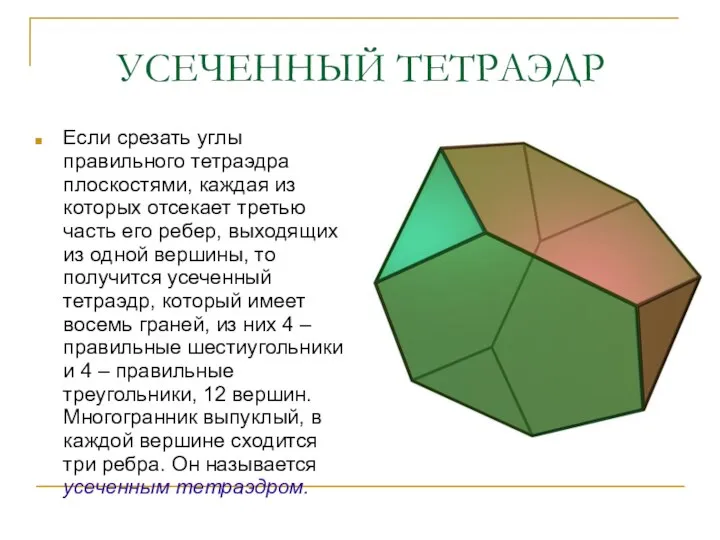
- 17. УСЕЧЕННЫЙ ТЕТРАЭДР Если срезать углы правильного тетраэдра плоскостями, каждая из которых отсекает третью часть его ребер,
- 18. УСЕЧЕННЫЙ ОКТАЭДР Если указанным образом срезать вершины октаэдра,то получим усеченный октаэдр.
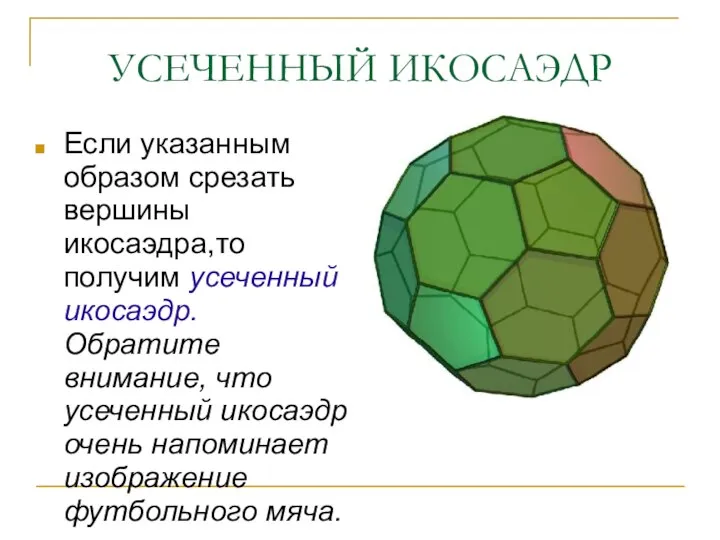
- 19. УСЕЧЕННЫЙ ИКОСАЭДР Если указанным образом срезать вершины икосаэдра,то получим усеченный икосаэдр. Обратите внимание, что усеченный икосаэдр
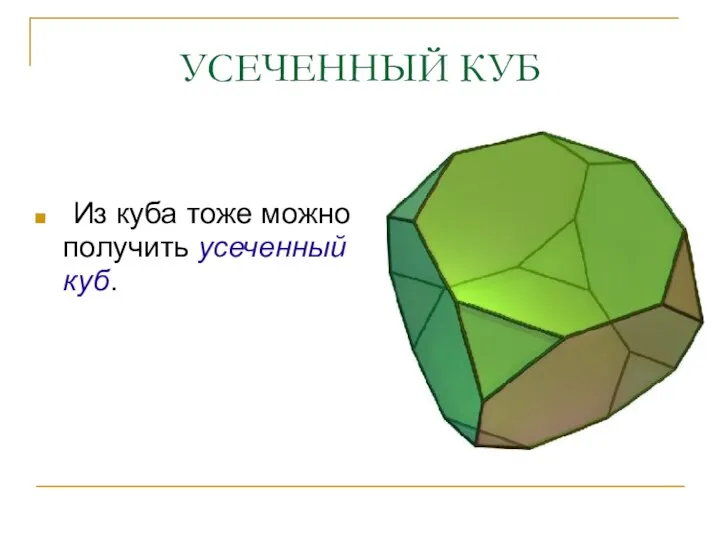
- 20. УСЕЧЕННЫЙ КУБ Из куба тоже можно получить усеченный куб.
- 21. УСЕЧЕННЫЙ ДОДЕКАЭДР Из додекаэдра тоже можно получить усеченный додекаэдр.
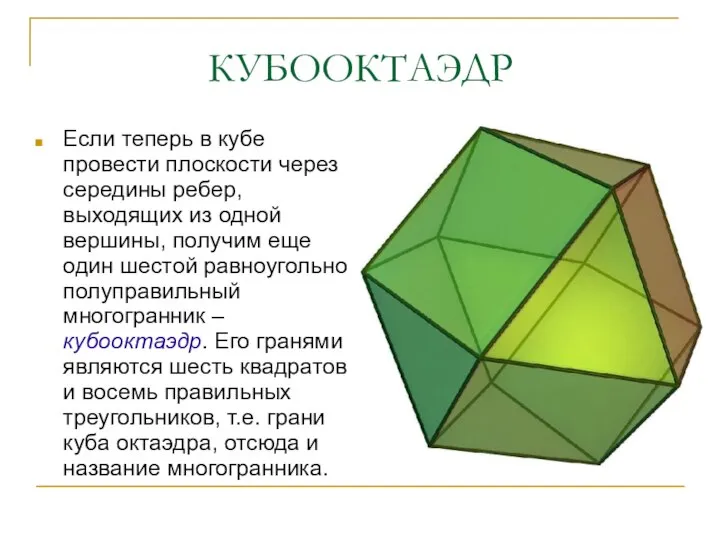
- 22. КУБООКТАЭДР Если теперь в кубе провести плоскости через середины ребер, выходящих из одной вершины, получим еще
- 23. ИКОСАДОДЕКАЭДР Аналогично, если в додекаэдре провести плоскости через середины его ребер, выходящих из одной вершины, получим
- 24. УСЕЧЕННЫЙ ИКОСАДОДЕКАЭДР К этим двум последним многогранникам также можно применять операцию «усечения» вершин. Получим усеченный кубооктаэдр
- 26. Скачать презентацию













 Правило умножения
Правило умножения Стохастические процессы
Стохастические процессы Закрепление знаний, умений и навыков решения задач на проценты
Закрепление знаний, умений и навыков решения задач на проценты Методические аспекты использования координатно – векторного метода при решении стереометрических задач
Методические аспекты использования координатно – векторного метода при решении стереометрических задач Виды многогранников
Виды многогранников Симметрия (9 класс) - презентация_
Симметрия (9 класс) - презентация_ Решение ГИА. (Задание 3)
Решение ГИА. (Задание 3) Использование эйдетики. (1 класс)
Использование эйдетики. (1 класс) Задачи по теме: «Смеси и сплавы». Подготовка к ЕГЭ. Профильный уровень. №11
Задачи по теме: «Смеси и сплавы». Подготовка к ЕГЭ. Профильный уровень. №11 Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Математика здоровья. Урок-игра для 8 класса
Математика здоровья. Урок-игра для 8 класса Презентация по математике "Задачи на проценты" - скачать бесплатно
Презентация по математике "Задачи на проценты" - скачать бесплатно Решение уравнений. ГИА 2014 Модуль «Алгебра» №4
Решение уравнений. ГИА 2014 Модуль «Алгебра» №4 Вписанная и описанная окружности
Вписанная и описанная окружности Центральные и вписанные углы. 8 класс
Центральные и вписанные углы. 8 класс Задачи о земледелии в горных районах
Задачи о земледелии в горных районах Часть II. Случайные величины
Часть II. Случайные величины Решение логарифмических уравнений
Решение логарифмических уравнений Метод подстановки
Метод подстановки По страницам учебника математики (8 класс)
По страницам учебника математики (8 класс) Графическое представление выборочного (эмпирического) распределения
Графическое представление выборочного (эмпирического) распределения Системы счисления
Системы счисления Коррекция СУ
Коррекция СУ Презентация к уроку математики в 4 классе. Тема: Закрепление по теме «Нумерация чисел больше 1000»
Презентация к уроку математики в 4 классе. Тема: Закрепление по теме «Нумерация чисел больше 1000» Интерактивная раскраска. Математическая игра для детей
Интерактивная раскраска. Математическая игра для детей Определители 2,3,n порядка. Тема 1
Определители 2,3,n порядка. Тема 1 Подготовка к ОГЭ. Методы, способствующие решению геометрических задач
Подготовка к ОГЭ. Методы, способствующие решению геометрических задач Элементы комбинаторики. 11 класс
Элементы комбинаторики. 11 класс