Содержание
- 2. Возрастание и убывание функции. Теорема (достаточные условия возрастания и убывания функции). Если то f(x) возрастает на
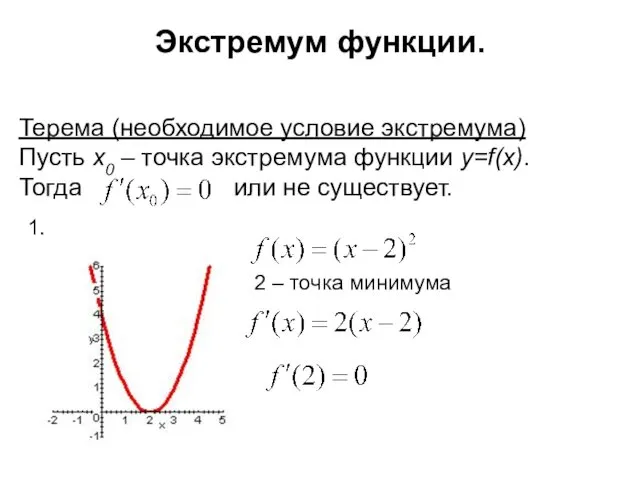
- 3. Экстремум функции. Терема (необходимое условие экстремума) Пусть x0 – точка экстремума функции y=f(x). Тогда или не
- 4. Экстремум функции. 0 – точка минимума 3. не существует
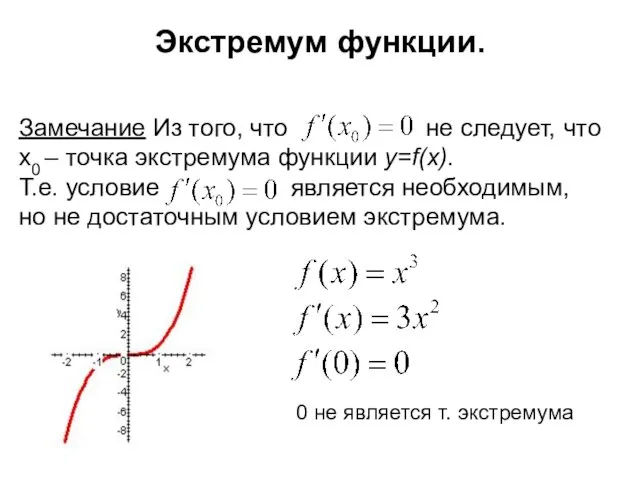
- 5. Экстремум функции. Замечание Из того, что не следует, что x0 – точка экстремума функции y=f(x). Т.е.
- 6. Экстремум функции. Опр. Точки, в которых производная равна 0 или не существует, называются критическими точками.
- 7. Экстремум функции. 1-е достаточное условие экстремума. Пусть - критическая точка функции y=f(x). Если при переходе через
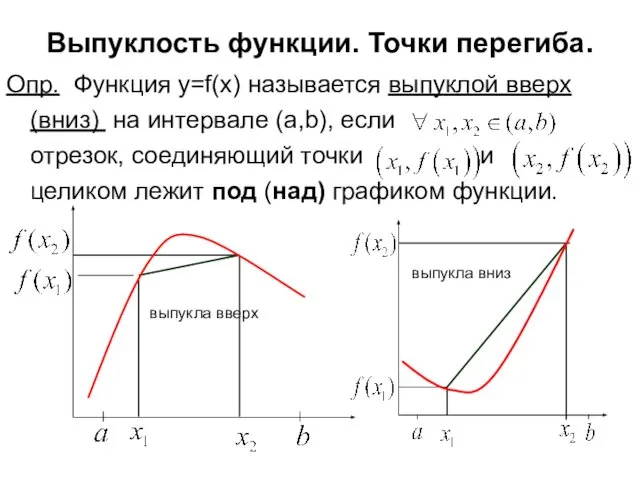
- 8. Опр. Функция y=f(x) называется выпуклой вверх (вниз) на интервале (a,b), если отрезок, соединяющий точки и целиком
- 9. Выпуклость функции. Точки перегиба. Теорема. Если то f(x) выпукла вниз на (a,b). Если то f(x) выпукла
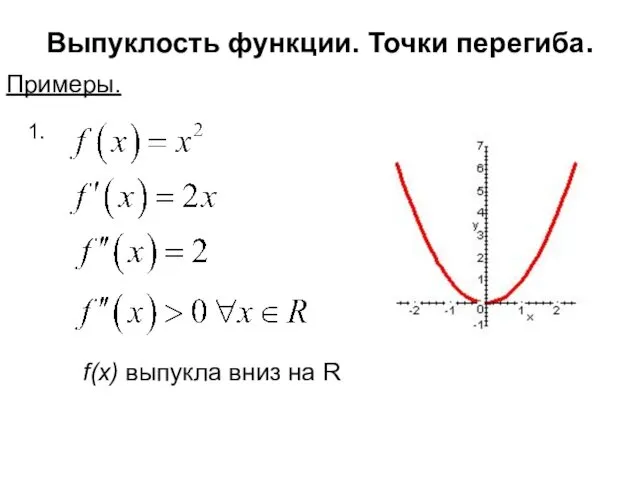
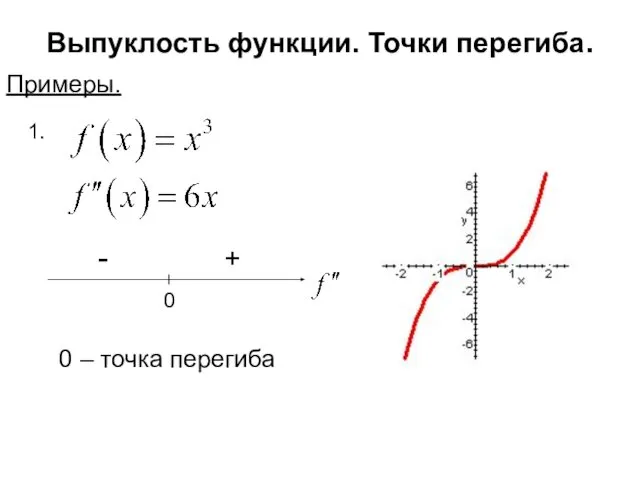
- 10. Выпуклость функции. Точки перегиба. Примеры. 1. f(x) выпукла вниз на R
- 11. Выпуклость функции. Точки перегиба. Примеры. 2. f(x) выпукла вверх на R
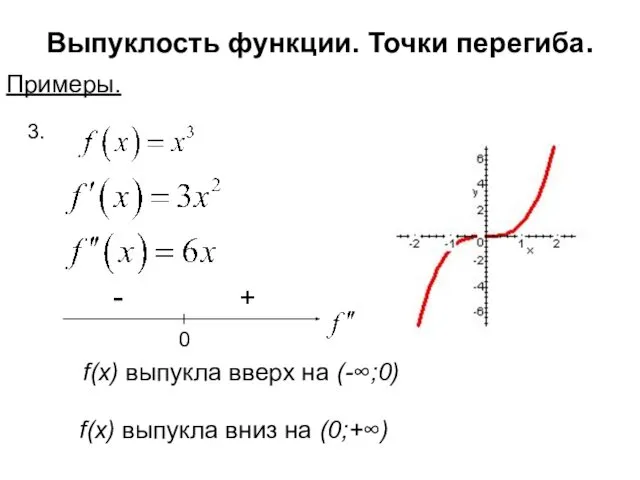
- 12. Выпуклость функции. Точки перегиба. Примеры. 3. f(x) выпукла вверх на (-∞;0) 0 + - f(x) выпукла
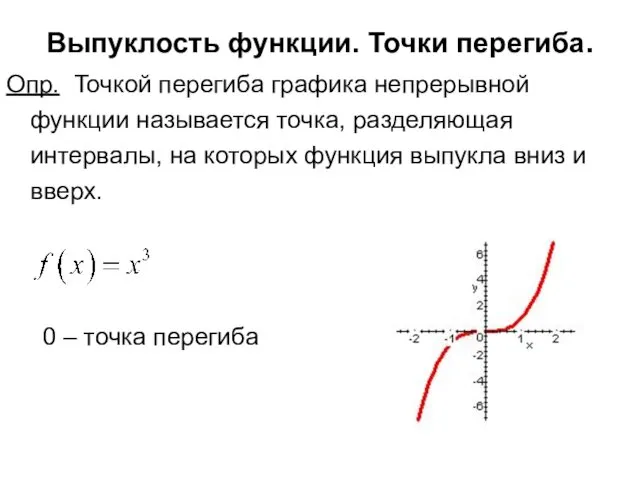
- 13. Выпуклость функции. Точки перегиба. Опр. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, на которых
- 14. Выпуклость функции. Точки перегиба. Теорема (необходимое условие перегиба) Если x0 – точка перегиба функции y=f(x), то
- 15. Выпуклость функции. Точки перегиба. Примеры. 1. 0 + - 0 – точка перегиба
- 17. Скачать презентацию







 Призначення й використання математичних і статистичних функцій табличного процесора
Призначення й використання математичних і статистичних функцій табличного процесора Итоговый тест по математике. 5 класс
Итоговый тест по математике. 5 класс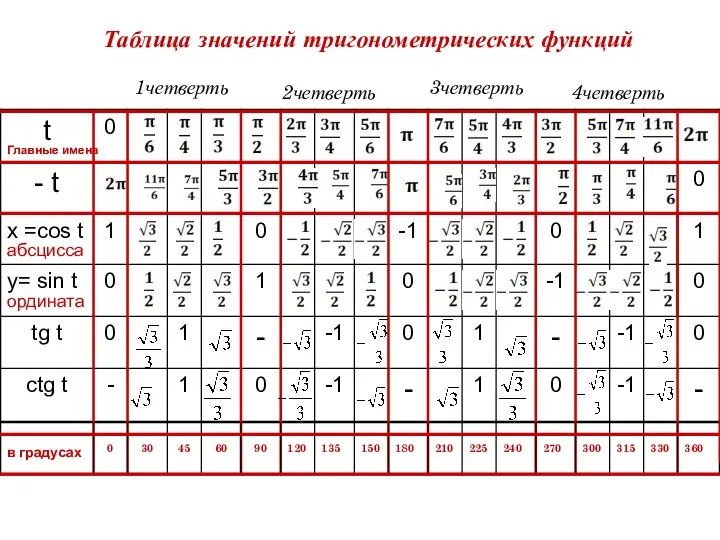 Таблица значений тригонометрических функций
Таблица значений тригонометрических функций 7 класста алгебра курсы буенча кабатлау дәресе
7 класста алгебра курсы буенча кабатлау дәресе Занимательные задачи по математике Автор проекта: Сё Александр Дмитриевич учащийся 4 класса Научный руководите
Занимательные задачи по математике Автор проекта: Сё Александр Дмитриевич учащийся 4 класса Научный руководите Аттестационная работа. Занимательная математика
Аттестационная работа. Занимательная математика Теорема Пифагора и различные способы её доказательства
Теорема Пифагора и различные способы её доказательства Презентация по математике "Решение простейших логарифмических неравенств" - скачать бесплатно
Презентация по математике "Решение простейших логарифмических неравенств" - скачать бесплатно Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом.
Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом.  ПРИЗНАКИ ДЕЛИМОСТИ 6 класс Сагайдакова Т.С. МОУ МСОШ №1
ПРИЗНАКИ ДЕЛИМОСТИ 6 класс Сагайдакова Т.С. МОУ МСОШ №1 Аттестационная работа. Числа великаны
Аттестационная работа. Числа великаны Поворот и параллельным перенос
Поворот и параллельным перенос Занимательная математика (средняя группа)
Занимательная математика (средняя группа) Определение окружности, ее основных элементов. Свойство касательной
Определение окружности, ее основных элементов. Свойство касательной Тригонометрические уравнения. Два основных метода решения тригонометрических уравнений
Тригонометрические уравнения. Два основных метода решения тригонометрических уравнений Интегрирование неотрицательніх измериміх функций
Интегрирование неотрицательніх измериміх функций Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Сравнение отрезков. Длина отрезка
Сравнение отрезков. Длина отрезка Сумма углов треугольника Решение задач
Сумма углов треугольника Решение задач  Презентация на тему ОСНОВНОЕ СВОЙСТВО ДРОБИ(математика 5 класс)
Презентация на тему ОСНОВНОЕ СВОЙСТВО ДРОБИ(математика 5 класс) Организация подготовки учащихся 5 класса к математическим олимпиадам с помощью решения задач. 5 класс
Организация подготовки учащихся 5 класса к математическим олимпиадам с помощью решения задач. 5 класс Элементы теории вероятностей
Элементы теории вероятностей Применение производной для исследования функций на монотонность
Применение производной для исследования функций на монотонность Линейные уравнения с одной переменной. Контрольная работа №2
Линейные уравнения с одной переменной. Контрольная работа №2 Многогранники. Решение задач
Многогранники. Решение задач Многогранники
Многогранники Оптимизация деятельности авторемонтного предприятия с помощью теории массового обслуживания
Оптимизация деятельности авторемонтного предприятия с помощью теории массового обслуживания Индивидуальный проект на тему “Построение сечений”
Индивидуальный проект на тему “Построение сечений”