Содержание
- 2. Метод введения новой переменной Метод сводится к замене тригонометрической функции новой переменной. Полученное уравнение решается известными
- 3. Пример 1. Решите уравнение:
- 4. Пример 1. Решение Введем новую переменную: Уравнение примет вид: отсюда находим ,
- 5. Пример 1. Решение Значит, либо , либо Первое уравнение не имеет корней, а из второго находим:
- 6. Пример 2. Решите уравнение:
- 7. Пример 2. Решение По основному тригонометрическому тождеству Получим: Введем новую переменную: Уравнение примет вид:
- 8. Пример 2. Решение Находим корни: , Отсюда: и Из первого уравнения Их второго находим Ответ: ,
- 9. Метод разложения на множители Если уравнение f(x)=0 удается преобразовать к виду f1(x)∙ f2(x)=0, то либо f1(x)=0
- 10. Пример 3. Решите уравнение:
- 11. Пример 3. Решение Вынесем общий множитель за скобку и получим: Приходим к совокупности двух уравнений:
- 12. Пример 3. Решение Решаем первое уравнение:
- 14. Скачать презентацию











 Аксиомы стереометрии и следствия из них. Математический диктант
Аксиомы стереометрии и следствия из них. Математический диктант Задачи по математике
Задачи по математике Многогранник пирамида
Многогранник пирамида Сложение и вычитание десятичных дробей. Обобщающий урок
Сложение и вычитание десятичных дробей. Обобщающий урок Векторы
Векторы Аттестационная работа. Рабочая программа элективного курса Начальные сведения из теории вероятностей
Аттестационная работа. Рабочая программа элективного курса Начальные сведения из теории вероятностей Презентация по математике "Первый признак равенства треугольников" - скачать бесплатно_
Презентация по математике "Первый признак равенства треугольников" - скачать бесплатно_ Организация и развитие внимания учащихся на уроках математики и во внеурочной деятельности
Организация и развитие внимания учащихся на уроках математики и во внеурочной деятельности Уравнения n-ой степени
Уравнения n-ой степени Временные ряды в эконометрических исследованиях
Временные ряды в эконометрических исследованиях Параллельные прямые. Решение задач
Параллельные прямые. Решение задач Простые и сложные проценты
Простые и сложные проценты Умножение и деление натуральных чисел
Умножение и деление натуральных чисел Факторный анализ
Факторный анализ Координатная плоскость (задачи)
Координатная плоскость (задачи) Относительные показатели: динамики, плана, координации
Относительные показатели: динамики, плана, координации Дифференцирование обратной функции
Дифференцирование обратной функции Решение задач на тему «Сумма углов треугольника»
Решение задач на тему «Сумма углов треугольника» Понятие производной. Сферы применения производной
Понятие производной. Сферы применения производной Тренажёр. Таблица умножения
Тренажёр. Таблица умножения Все действия с натуральными числами. Урок-путешествие к острову натуральных чисел
Все действия с натуральными числами. Урок-путешествие к острову натуральных чисел Глава 9. Элементы математической статистики, комбинаторики и теории вероятностей §53. Формула бинома Ньютона
Глава 9. Элементы математической статистики, комбинаторики и теории вероятностей §53. Формула бинома Ньютона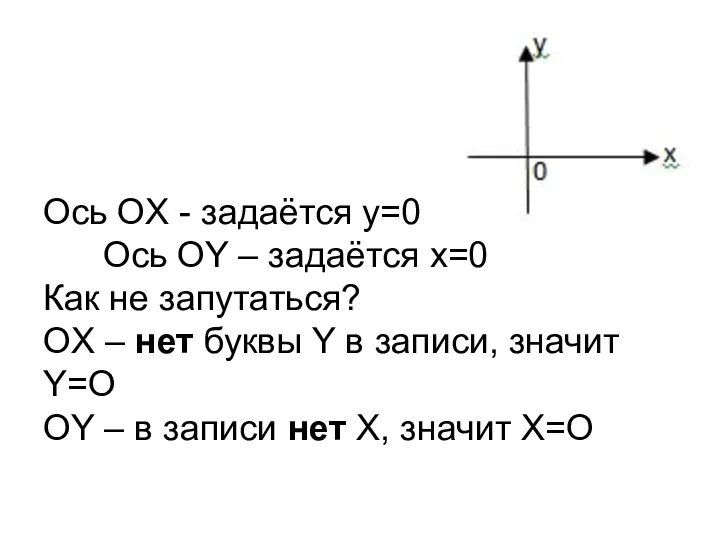 Построение оси координат
Построение оси координат Статистичні помилки. Статистичні гіпотези та їх перевірка. Параметричні і непараметричні критерії перевірки
Статистичні помилки. Статистичні гіпотези та їх перевірка. Параметричні і непараметричні критерії перевірки Подобные треугольники
Подобные треугольники ОГЭ математика вариант 14
ОГЭ математика вариант 14 Из истории отрицательных чисел
Из истории отрицательных чисел Презентация по математике "Счёт в 1 классе" - скачать бесплатно
Презентация по математике "Счёт в 1 классе" - скачать бесплатно