Содержание
- 2. Применение дифференциала для приближенных вычислений. Из определения производной функции: Можно записать: , или . Величина -
- 3. Пример: вычислить без таблицы Sin29 ͦ Sin29 ͦ=Sin(30 ͦ-1 ͦ), поэтому примем x=30 ͦ, а Δx=-1
- 4. Частные производные функций
- 5. Частные и полный дифференциал функции
- 6. Задача: найдите абсолютную погрешность в определении объема цилиндра, если при измерениях были получены радиуса r= (6±0,1)
- 7. Интегральное исчисление. Первообразная функция. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если
- 8. Неопределенный интеграл. Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) +
- 10. Свойства: где u, v, w – некоторые функции от х. Пример:
- 11. Методы интегрирования А) Непосредственное интегрирование.
- 12. Б) Способ подстановки (замены переменных).
- 13. В) Интегрирование по частям.
- 14. Пример. Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному
- 16. Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)
- 17. Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x)
- 18. Свойства определенного интеграла. 4. Если f(x) ≤ ϕ(x) на отрезке [a, b] a
- 19. 5.Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b],
- 20. 8. Для произвольных чисел a, b, c справедливо равенство: Теорема: (Теорема Ньютона – Лейбница) Если функция
- 21. Пример.
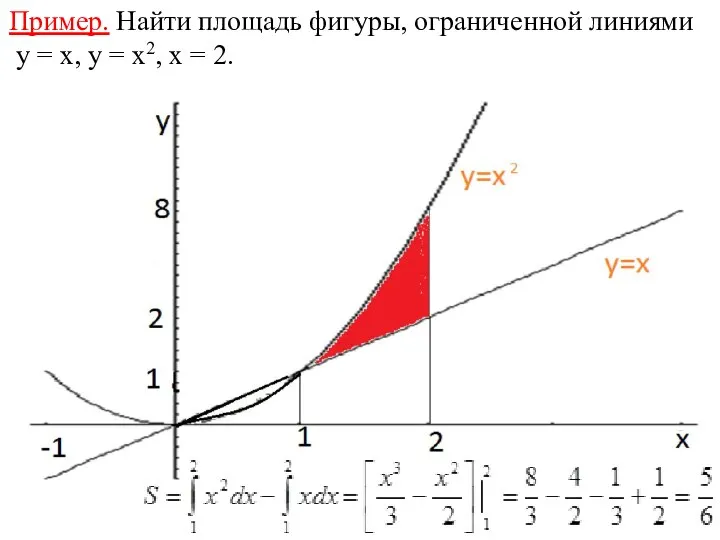
- 22. Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
- 23. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 26. Скачать презентацию







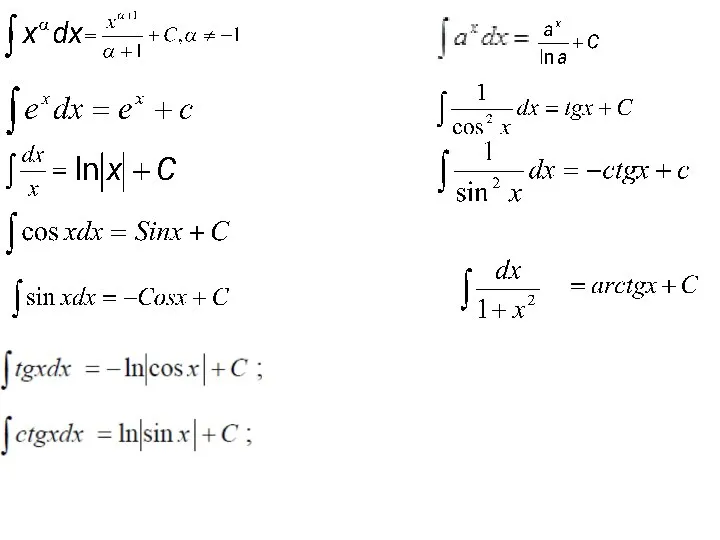





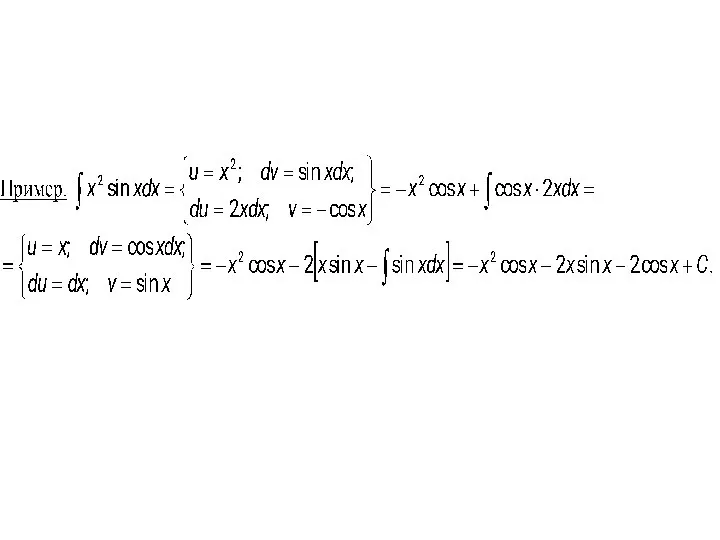
![Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1469931/slide-15.jpg)

![Свойства определенного интеграла. 4. Если f(x) ≤ ϕ(x) на отрезке [a, b] a](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1469931/slide-17.jpg)





 Сумма углов треугольника
Сумма углов треугольника Figures of matching
Figures of matching Аттестационная работа. Подготовка к итоговой аттестации по математике в новой форме. (9 класс)
Аттестационная работа. Подготовка к итоговой аттестации по математике в новой форме. (9 класс) Великая теорема Ферма
Великая теорема Ферма Построение графика функци y= x
Построение графика функци y= x Формы графического изображения. (Лекция 3)
Формы графического изображения. (Лекция 3) Косинус угла
Косинус угла Поворот и параллельный перенос
Поворот и параллельный перенос Дифференциальные уравнения 2-го порядка Лекция 5
Дифференциальные уравнения 2-го порядка Лекция 5  Основы теории логических преобразований
Основы теории логических преобразований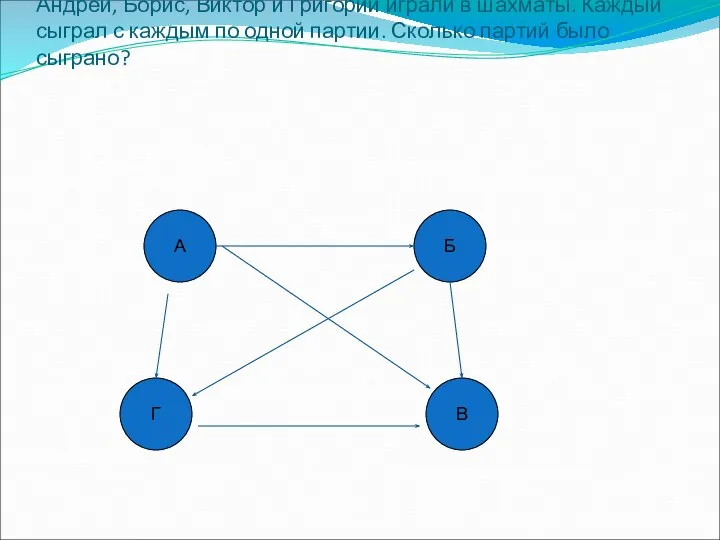 Решение задач с помощью графов
Решение задач с помощью графов Раскрытие скобок
Раскрытие скобок Иррациональные уравнения
Иррациональные уравнения Математика «Четырехзначные числа» «Величины» «Умножение в пределах 100» 3 класс Н.Б.Истомина тесты
Математика «Четырехзначные числа» «Величины» «Умножение в пределах 100» 3 класс Н.Б.Истомина тесты Математический ералаш
Математический ералаш Проценты в жизни человека. 5 класс
Проценты в жизни человека. 5 класс Применение производной к исследованию функции
Применение производной к исследованию функции Кроссворд по геометрии
Кроссворд по геометрии Частные производные функции
Частные производные функции Вписанные и описанные окружности
Вписанные и описанные окружности Мастер-класс Решение задач по геометрии при подготовке к ОГЭ
Мастер-класс Решение задач по геометрии при подготовке к ОГЭ Графики. График движения
Графики. График движения Вынесение множителя из-под знака корня. Внесение множителя под знак корня
Вынесение множителя из-под знака корня. Внесение множителя под знак корня Нахождение свойств производной по графику функции (№7 ЕГЭ)
Нахождение свойств производной по графику функции (№7 ЕГЭ) Линейные дифференциальные уравнения 1-ого порядка
Линейные дифференциальные уравнения 1-ого порядка Задачи. Ломаная линия
Задачи. Ломаная линия Математический вечер Ох, уж эта математика
Математический вечер Ох, уж эта математика Нахождение числа по значению его дроби
Нахождение числа по значению его дроби