Содержание
- 2. 1 задача Плоскость разделена прямыми на несколько частей. Какое наименьшее количество цветов нужно для раскраски получившихся
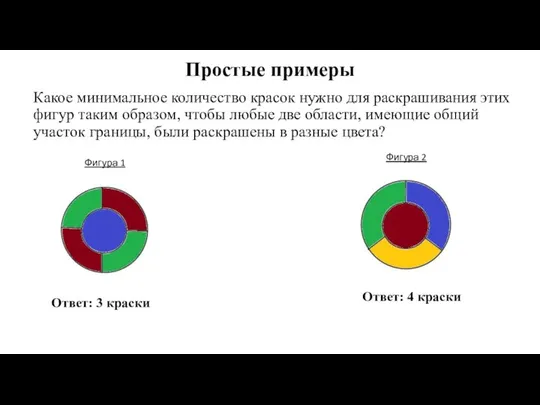
- 3. Простые примеры Какое минимальное количество красок нужно для раскрашивания этих фигур таким образом, чтобы любые две
- 4. Можно ли всякую расположенную на плоскости карту раскрасить 4 красками так, чтобы любые две области, имеющие
- 5. Немного истории Теорему о четырех красках открыл в 1852 году Френсис Гутри, составляя карту графств Англии.
- 6. Задача-обобщение Ответ: если х нечетно, то 4, если х четно, то 3. Рассмотрим фигуру с неизвестным
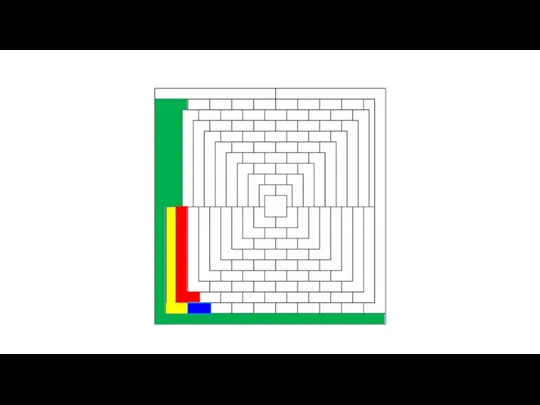
- 7. Попробуйте раскрасить фигуру, используя наименьшее возможное количество цветов таким образом, чтобы любые две области, имеющие общий
- 10. 2 задача То что вы использовали в предыдущих задачах, применимо и для объемных фигур. Например, сколько
- 11. Игра «4 краски» Пример законченной игры Игра "Четыре краски" придумана по мотивам этой теоремы. Игровое поле
- 12. Спасибо за внимание!
- 13. Раздаточный материал
- 14. 1 задача Плоскость разделена прямыми на несколько частей. Какое наименьшее количество цветов нужно для раскраски получившихся
- 15. Простые примеры Фигура 1 Фигура 2 Какое минимальное количество красок нужно для раскрашивания этих фигур таким
- 16. Задача-обобщение Рассмотрим фигуру с неизвестным количеством «перегородок» - Х. Определите зависимость количества необходимых цветов при изменении
- 17. Задача с многоугольниками Попробуйте раскрасить фигуру, используя наименьшее возможное количество цветов таким образом, чтобы любые две
- 19. Скачать презентацию














 Пример решения задачи по оценке эффективности использования основных средств. Задание 9.4
Пример решения задачи по оценке эффективности использования основных средств. Задание 9.4 В поисках клада! Интерактивное занятие по математике в средней группе
В поисках клада! Интерактивное занятие по математике в средней группе Игра. Математический бой
Игра. Математический бой Квадратичная функция. Её свойства и график
Квадратичная функция. Её свойства и график Сложение и вычитание векторов
Сложение и вычитание векторов Что такое функции
Что такое функции Центральная симметрия. Осевая симметрия
Центральная симметрия. Осевая симметрия Методика решения текстовых задач
Методика решения текстовых задач Одночлены 7 класс Бралгина Наталья Михайловна МАОУ СОШ п.Демянск 2011-2012 уч.год
Одночлены 7 класс Бралгина Наталья Михайловна МАОУ СОШ п.Демянск 2011-2012 уч.год  Повышение качества обучения математики с учетом результатов ГИА (ЕГЭ) в 2021 году
Повышение качества обучения математики с учетом результатов ГИА (ЕГЭ) в 2021 году Здоровье. Задачи по математике. 5-9 класс
Здоровье. Задачи по математике. 5-9 класс Призма
Призма  Проверка деления с остатком
Проверка деления с остатком Виды показательных уравнений и способы их решения
Виды показательных уравнений и способы их решения Формулы двойного угла
Формулы двойного угла Экстремумы функции. Применение производной к исследованию функций
Экстремумы функции. Применение производной к исследованию функций Производная функции
Производная функции Объемы. Объем прямоугольного параллелепипеда
Объемы. Объем прямоугольного параллелепипеда Построение графика квадратичной функции у(х)= ах2 + вх + с
Построение графика квадратичной функции у(х)= ах2 + вх + с Бенефис линейной функции. 7 класс
Бенефис линейной функции. 7 класс Презентация по математике "Разность и сумма" - скачать бесплатно
Презентация по математике "Разность и сумма" - скачать бесплатно Презентация по математике "Вычисления с многозначными числами" - скачать
Презентация по математике "Вычисления с многозначными числами" - скачать  Сравнение бесконечно малых и бесконечно больших величин
Сравнение бесконечно малых и бесконечно больших величин Тіла обертання
Тіла обертання Диаграммы в Excel
Диаграммы в Excel Прямая и обратная пропорциональность. Определение, примеры, задачи
Прямая и обратная пропорциональность. Определение, примеры, задачи Классическое определение вероятности события
Классическое определение вероятности события Тригонометрические формулы. 10 класс
Тригонометрические формулы. 10 класс