Содержание
- 2. Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос,
- 3. Производная — это скорость изменения функции.
- 4. На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
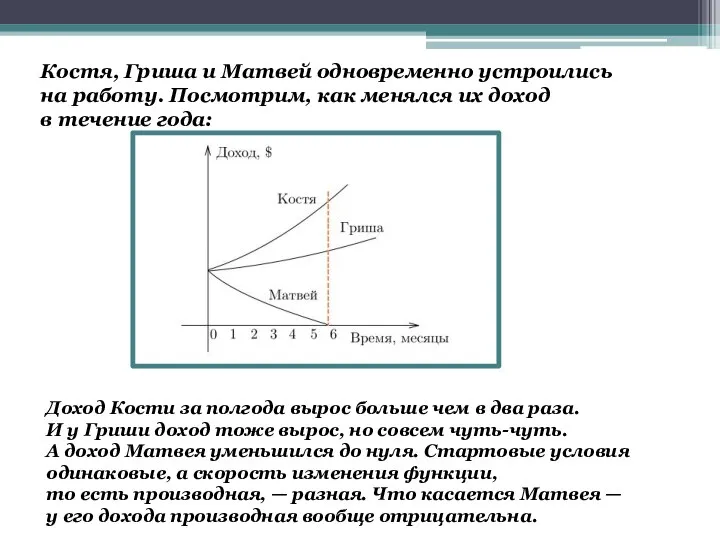
- 5. Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
- 6. Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем? На самом деле
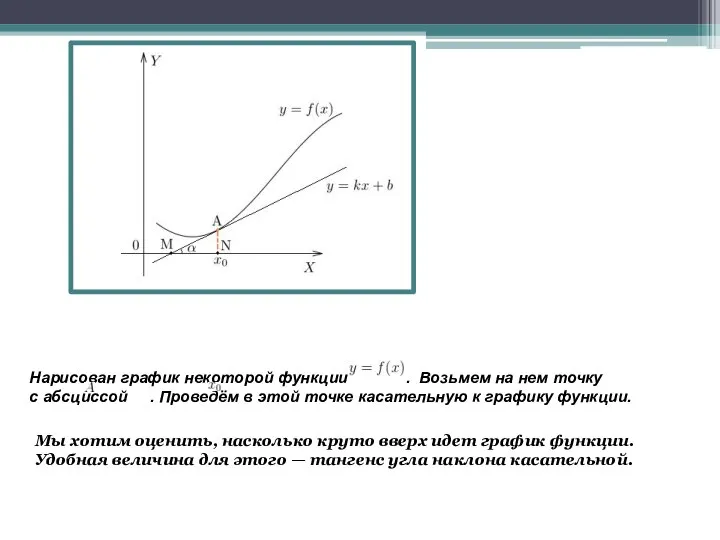
- 7. Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке
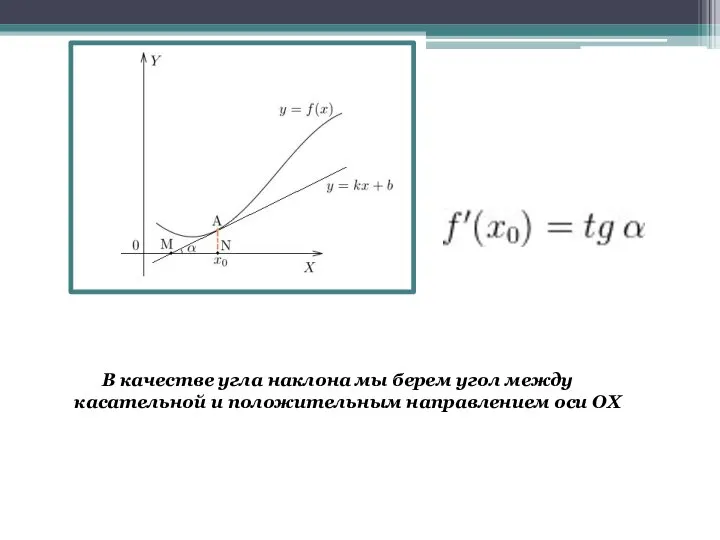
- 8. В качестве угла наклона мы берем угол между касательной и положительным направлением оси OX
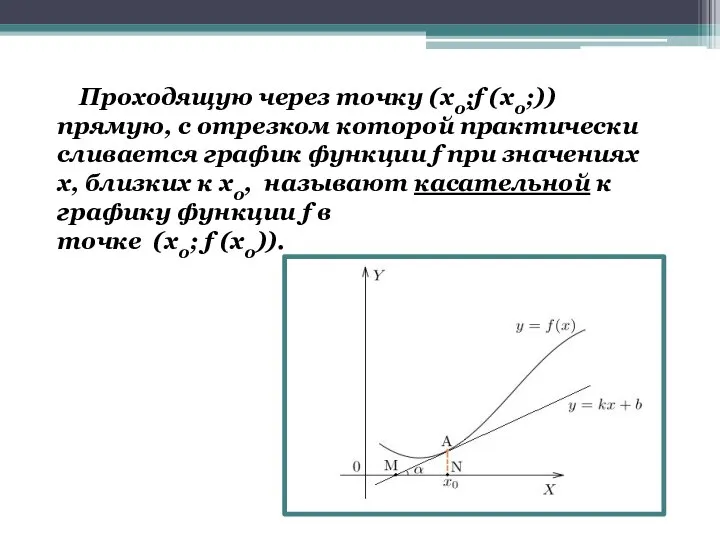
- 9. Проходящую через точку (x0;f (x0;)) прямую, с отрезком которой практически сливается график функции f при значениях
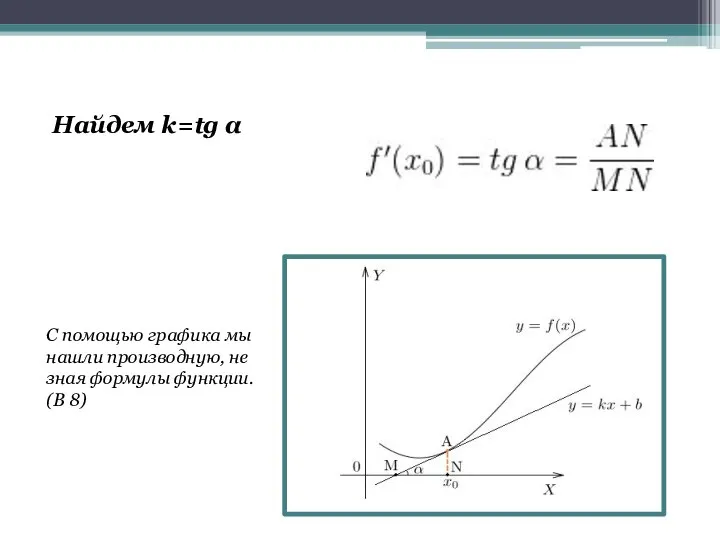
- 10. Найдем k=tg α С помощью графика мы нашли производную, не зная формулы функции. (В 8)
- 11. Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная
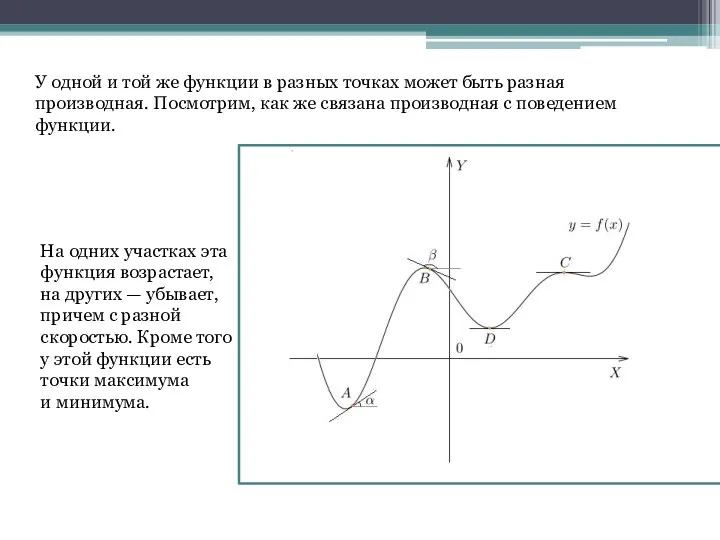
- 12. У одной и той же функции в разных точках может быть разная производная. Посмотрим, как же
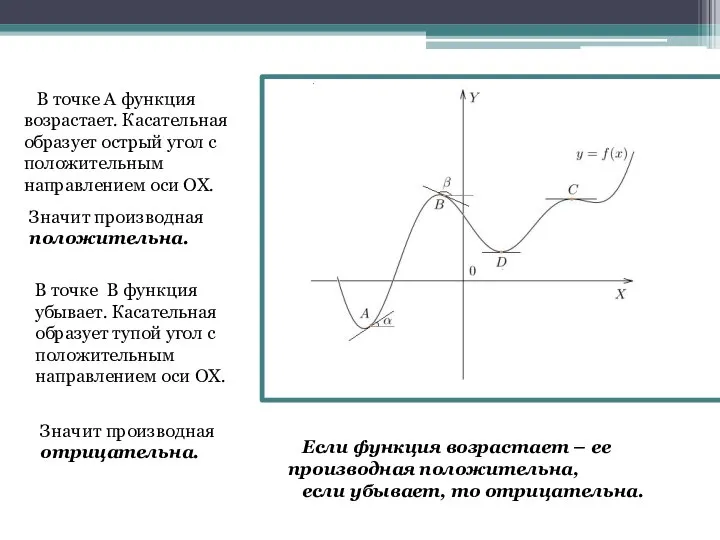
- 13. В точке А функция возрастает. Касательная образует острый угол с положительным направлением оси ОХ. Значит производная
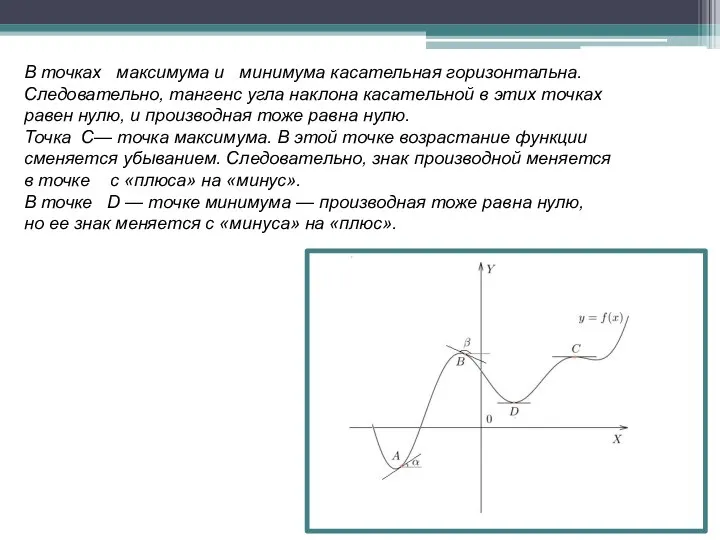
- 14. В точках максимума и минимума касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен
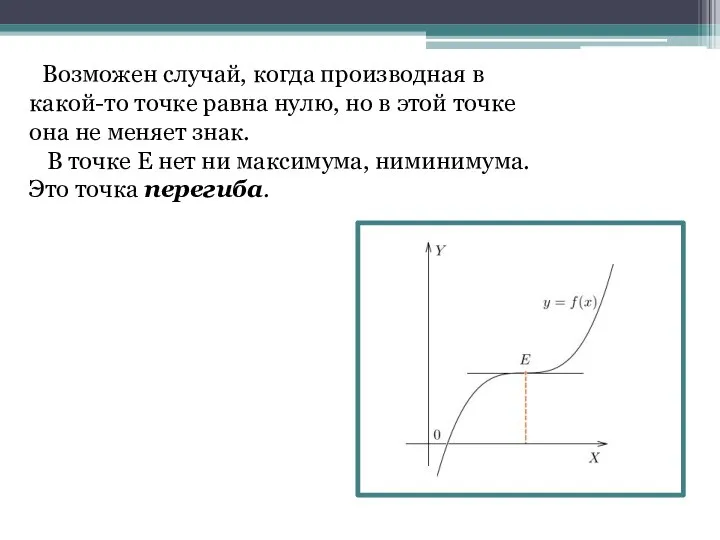
- 16. Возможен случай, когда производная в какой-то точке равна нулю, но в этой точке она не меняет
- 18. Скачать презентацию






 «В здоровом теле- здоровый ум» _
«В здоровом теле- здоровый ум» _ Арифметический диктант. Математика
Арифметический диктант. Математика Спираль Архимеда
Спираль Архимеда Графический способ решения систем уравнений
Графический способ решения систем уравнений Прямоугольник и квадрат
Прямоугольник и квадрат Презентация по математике "Замысловатые маршруты Эйлера" - скачать
Презентация по математике "Замысловатые маршруты Эйлера" - скачать  Задачи с параметрами
Задачи с параметрами Тела вращения
Тела вращения Презентация по математике "Самостоятельная работа" - скачать бесплатно
Презентация по математике "Самостоятельная работа" - скачать бесплатно Геометрическая и арифметическая прогрессии
Геометрическая и арифметическая прогрессии Простейшие вероятностные задачи
Простейшие вероятностные задачи Примеры решения неравенств
Примеры решения неравенств Линейная функция и её график
Линейная функция и её график Коэффициент корреляции и корреляционный анализ
Коэффициент корреляции и корреляционный анализ ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ
ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ Понятие смешанной дроби. 5 класс
Понятие смешанной дроби. 5 класс Конкурс Веселых, Умных, Находчивых
Конкурс Веселых, Умных, Находчивых Презентация по математике "Применение производной в физике, математике, биологии и жизни" - скачать
Презентация по математике "Применение производной в физике, математике, биологии и жизни" - скачать  Формула квадрат суммы двух выражений:
Формула квадрат суммы двух выражений: Использование теории подобных треугольников при решении разнообразных задач
Использование теории подобных треугольников при решении разнообразных задач Смешанные числа
Смешанные числа Обобщенный эвристический алгоритм
Обобщенный эвристический алгоритм Понятие арифметического квадратного корня
Понятие арифметического квадратного корня Определение арифметического корня п-ой степени
Определение арифметического корня п-ой степени Задачи экономического содержания на ЕГЭ
Задачи экономического содержания на ЕГЭ Повторение по теме: «Натуральные числа»
Повторение по теме: «Натуральные числа» Корреляционно-регрессионный анализ в экономическом прогнозировании
Корреляционно-регрессионный анализ в экономическом прогнозировании Предел функции
Предел функции