Содержание
- 2. Принцип 80/20 20% ассортимента продукции - 80% от общего объема продаж 20% покупателей и клиентов -
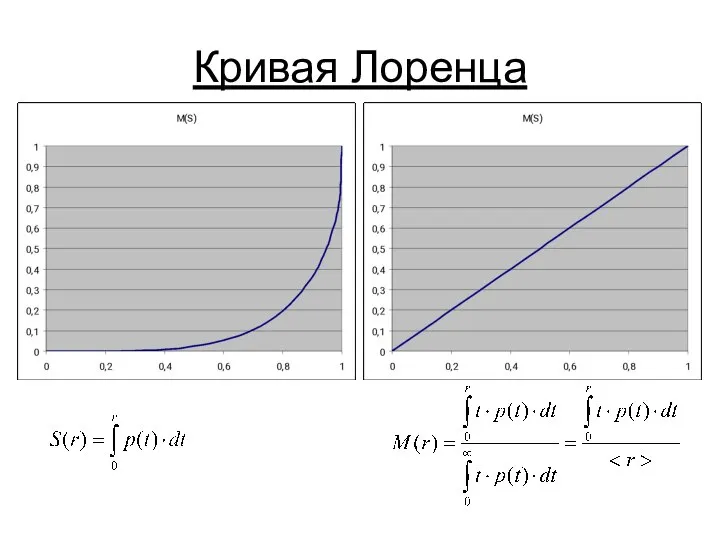
- 3. Кривая Лоренца
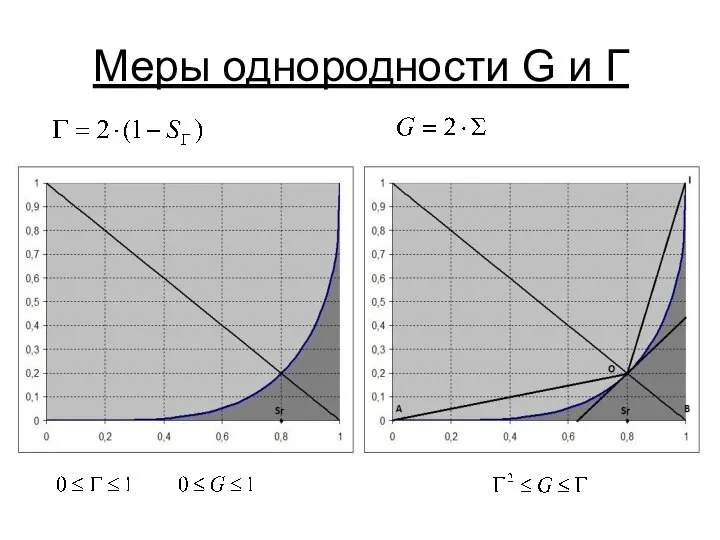
- 4. Меры однородности G и Г
- 5. Три меры неоднородности Меры Г и G "работают" только для неотрицательных "r" - мера Ф работает
- 6. Свойства меры однородности G
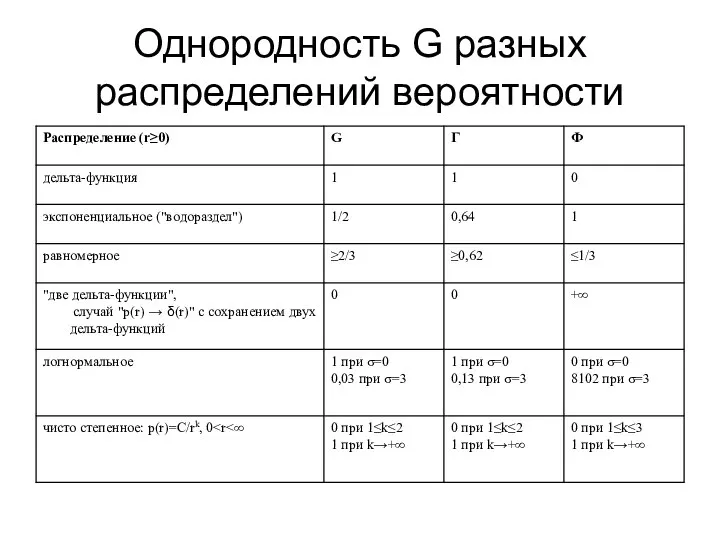
- 7. Однородность G разных распределений вероятности
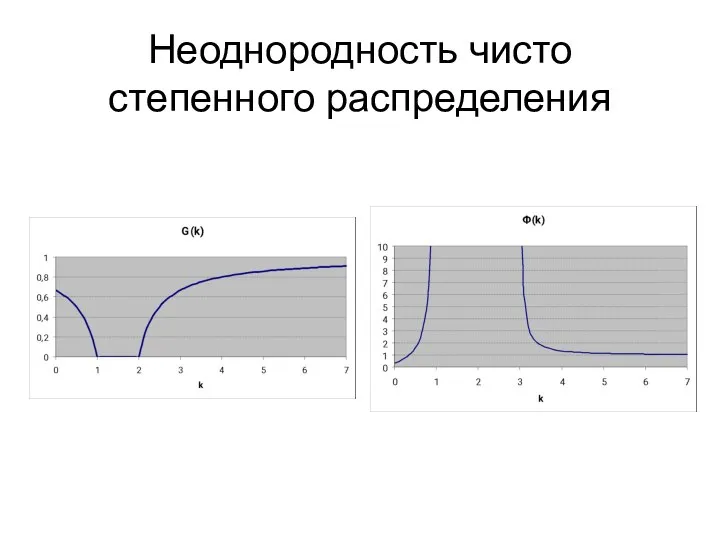
- 8. Неоднородность чисто степенного распределения
- 9. Модель эффекта случайных смещений результата Можно условно считать, что: добавление нового параметра "у" увеличивает дисперсию и
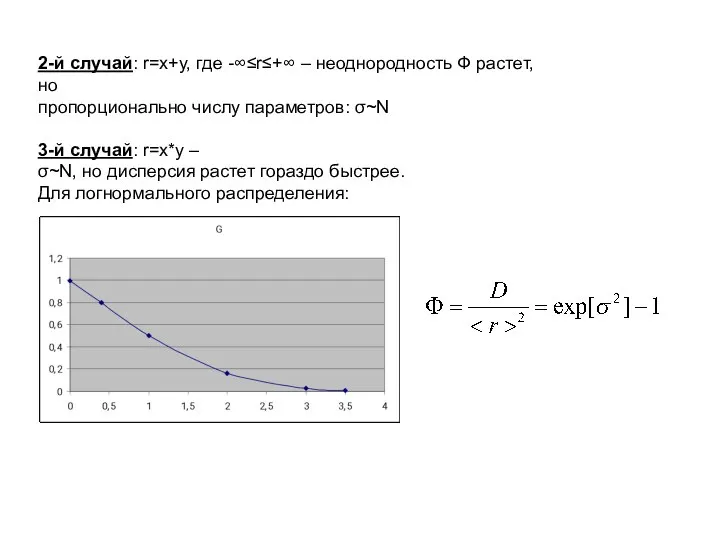
- 10. 2-й случай: r=x+y, где -∞≤r≤+∞ – неоднородность Ф растет, но пропорционально числу параметров: σ~N 3-й случай:
- 11. Эффект естественного отбора "Побеждают сильнейшие": G = результат усреднения однородности Gi "гармоник" с весовым коэффициентом ki~(
- 12. ЭЕО: Большая неоднородность Скалярное произведение порождает сепарабельное гильбертово пространство:
- 13. Поведение меры однородности G при суммировании гармоник Сумма гармоник: - "длина вектора" То есть побеждают наибольшие
- 14. ЭЕО: Появление "степенных хвостов" распределений Эффективный показатель степени: "Степенное усреднение": В дискретном случае:
- 15. Дрейф показателя суммы гармоник вниз вплоть до наименьшего из показателей "Степенная дисперсия":
- 16. Отклонение эфф-го показателя степени от минимального
- 17. Эффективный показатель степени для конечных результатов
- 18. "Чистые" законы распределения не объясняются эффектом естественного отбора объясняются эффектом случайных смещений параметра только для некоторых
- 19. Условие сокрытия параметров для марковских процессов - произвольная функция
- 20. Чисто степенные распределения для марковских процессов Разумно предположить, что если в результате эволюции получается чисто степенное
- 22. Скачать презентацию














 Показательные уравнения и способы их решения
Показательные уравнения и способы их решения Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы решения систем линейных уравнений Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Муниципальное бюджетное общеобразовательное учреждение «Дрезненская гимназия» ШУТКА ГЕНИЕВ: ФЛЕКСАГОН Выполнила: Маркина Диа
Муниципальное бюджетное общеобразовательное учреждение «Дрезненская гимназия» ШУТКА ГЕНИЕВ: ФЛЕКСАГОН Выполнила: Маркина Диа Урок математики 3 класс Умножение числа 8, умножение на 8
Урок математики 3 класс Умножение числа 8, умножение на 8 Применение подобия для решения задач
Применение подобия для решения задач Көп Факторлы дисперсиялық талдау. Көп факторлы дисперсиялық талдаудың бір факторлы дисперсиялық талдаудан айырмашылығы
Көп Факторлы дисперсиялық талдау. Көп факторлы дисперсиялық талдаудың бір факторлы дисперсиялық талдаудан айырмашылығы Решение уравнений
Решение уравнений АНАЛИЗ СОДЕРЖАНИЯ ЗАДАНИЙ ПО МАТЕМАТИКЕ ЕГЭ
АНАЛИЗ СОДЕРЖАНИЯ ЗАДАНИЙ ПО МАТЕМАТИКЕ ЕГЭ  Геометрические фигуры
Геометрические фигуры Треугольник. Правило треугольника
Треугольник. Правило треугольника Решение уравнений
Решение уравнений Приближенное значение величины. Абсолютная и относительная погрешность
Приближенное значение величины. Абсолютная и относительная погрешность Геометрические задачи С4, по материалам ЕГЭ. Подобие треугольников
Геометрические задачи С4, по материалам ЕГЭ. Подобие треугольников Трофеи от Аничкова
Трофеи от Аничкова Решение задач на применение признаков равенства треугольников
Решение задач на применение признаков равенства треугольников Двогранний кут
Двогранний кут Умножение двузначного числа на однозначное
Умножение двузначного числа на однозначное Математический диктант. Решите уравнения
Математический диктант. Решите уравнения Планирование эксперимента. Анализ результатов. Планирование 2-го порядка
Планирование эксперимента. Анализ результатов. Планирование 2-го порядка Презентация по математике "Дробь как одна или несколько равных долей" - скачать
Презентация по математике "Дробь как одна или несколько равных долей" - скачать  решение неравенств с одной переменной
решение неравенств с одной переменной Готовимся к ГИА, 9 класс. Тест 4, часть 1
Готовимся к ГИА, 9 класс. Тест 4, часть 1 Контрольная работа. Вариант №0
Контрольная работа. Вариант №0 Измерение площади и объёма
Измерение площади и объёма Решение квадратных уравнений
Решение квадратных уравнений Тригонометрические функции угла (00 – 1800)
Тригонометрические функции угла (00 – 1800) Формулы сокращенного умножения
Формулы сокращенного умножения