Содержание
- 2. При решении логарифмических неравенств можно использовать условия равносильности. Преимущество использования условий равносильности по сравнению с обычным
- 3. Для неравенств вида loga f(x)> 0( Правило 1: Знак loga f(x) совпадает со знаком произведения в
- 4. Используя это правило, можно записать условие равносильности, включающее ОДЗ для строгих логарифмических неравенств: loga f(x)> 0(
- 5. для нестрогих логарифмических неравенств:
- 6. Для логарифмических неравенств вида loga f(x) > loga g(x) и более сложных существует Правило 2. Знак
- 7. Используя Правило 2, можно записать условие равносильности, включающее ОДЗ для неравенств вида:
- 8. Также можно очень просто решить более сложные неравенства, используя Правило 2, например: в ОДЗ.
- 9. Очень важно, что освобождение от всех логарифмов происходит за один шаг. Использование данных правил сводит решение
- 10. Рассмотрим применение Правила 1 на примере. Решим логарифмическое неравенство:
- 12. Найдем ОДЗ: Применяя метод интервалов, найдем общее решение данной системы:
- 13. По Правилу 1 знак совпадает со знаком произведения а знак со знаком Поэтому в ОДЗ имеем:
- 15. Применяя метод интервалов, получим решение данного неравенства: Найдем общее решение исходного неравенства с учетом ОДЗ. Ответ:
- 16. Таким образом, использование данных правил, позволяет просто справиться с логарифмическими неравенствами, решение которых обычным способом потребует
- 18. Скачать презентацию









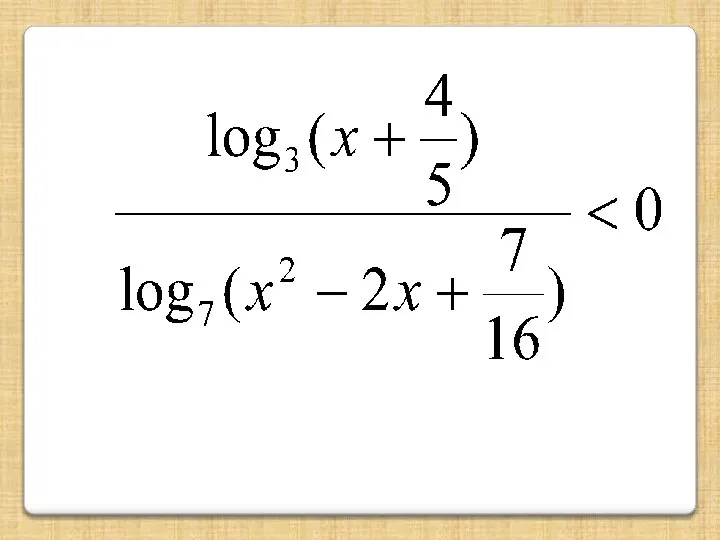





 Алгебраические выражения
Алгебраические выражения Аттестационная работа. Нестандартные методы решения квадратных уравнений
Аттестационная работа. Нестандартные методы решения квадратных уравнений Аттестационная работа. Образовательная программа элективного курса по математике «Решение типовых задач»
Аттестационная работа. Образовательная программа элективного курса по математике «Решение типовых задач» Расстояние от точки до прямой. Расстояние между параллельными прямыми
Расстояние от точки до прямой. Расстояние между параллельными прямыми Сложение обыкновенных дробей. Устно для 6 кл
Сложение обыкновенных дробей. Устно для 6 кл Классическое определение теории вероятности. Основные понятия теории вероятности.
Классическое определение теории вероятности. Основные понятия теории вероятности.  Урок 105. Признаки делимости на 2, 5, 10, 4 и 25. Урок 105
Урок 105. Признаки делимости на 2, 5, 10, 4 и 25. Урок 105 Равносильность неравенств
Равносильность неравенств Натуральные числа и нуль. Ряд натуральных чисел. Десятичная система записи натуральных чисел
Натуральные числа и нуль. Ряд натуральных чисел. Десятичная система записи натуральных чисел Презентация по математике "Старинные единицы измерения" - скачать бесплатно
Презентация по математике "Старинные единицы измерения" - скачать бесплатно Прототипы В 14. Исследование сложной функции, содержащей показательную, логарифмическую функции и функцию квадратный корень
Прототипы В 14. Исследование сложной функции, содержащей показательную, логарифмическую функции и функцию квадратный корень Тест. Задания В13, ЕГЭ по математике
Тест. Задания В13, ЕГЭ по математике Первообразная функции и неопределенный интеграл
Первообразная функции и неопределенный интеграл Презентация по математике "Устный счет" - скачать бесплатно_
Презентация по математике "Устный счет" - скачать бесплатно_ Разложение чисел на простые множители
Разложение чисел на простые множители Повторение курса геометрии (часть 1)
Повторение курса геометрии (часть 1) Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Кривые 2-го порядка: эллипс, гипербола, парабола
Кривые 2-го порядка: эллипс, гипербола, парабола Паралельність прямих і площин у простор
Паралельність прямих і площин у простор История возникновения чисел
История возникновения чисел Пирамида. Правильная пирамида
Пирамида. Правильная пирамида Десятичные и обыкновенные дроби
Десятичные и обыкновенные дроби Аттестационная работа. Образовательная программа курса внеурочной деятельности для 6-х классов «Занимательная математика»
Аттестационная работа. Образовательная программа курса внеурочной деятельности для 6-х классов «Занимательная математика» Длина окружности
Длина окружности Математика 4 класс Добрый день, дорогие ребята!
Математика 4 класс Добрый день, дорогие ребята! Математический квест. Путешествие в замке П
Математический квест. Путешествие в замке П Экстремум функции нескольких переменных. Наибольшее и наименьшее значения функции в замкнутой области. Лeкция №6-7
Экстремум функции нескольких переменных. Наибольшее и наименьшее значения функции в замкнутой области. Лeкция №6-7 Особенности преподавания математики в 5 классе в современных условиях развития образования
Особенности преподавания математики в 5 классе в современных условиях развития образования