Содержание
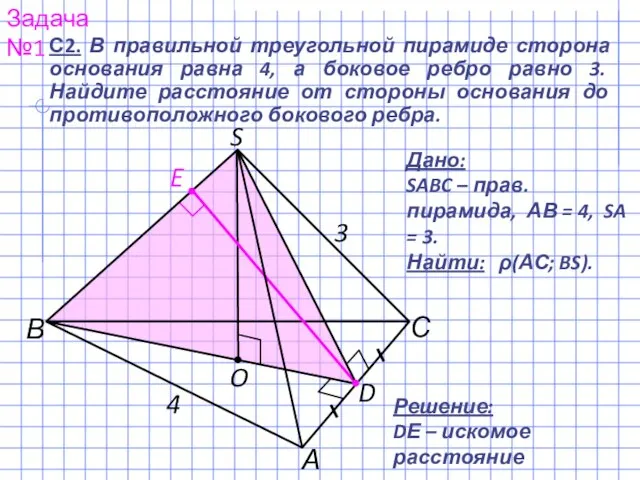
- 2. С2. В правильной треугольной пирамиде сторона основания равна 4, а боковое ребро равно 3. Найдите расстояние
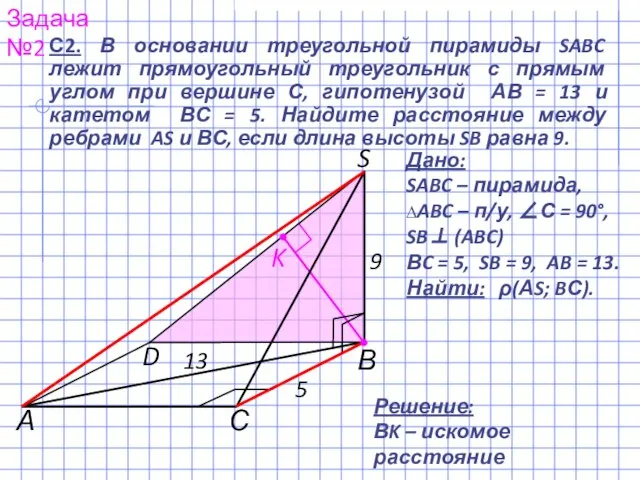
- 3. S В С А D 13 5 9 K С2. В основании треугольной пирамиды SABC лежит
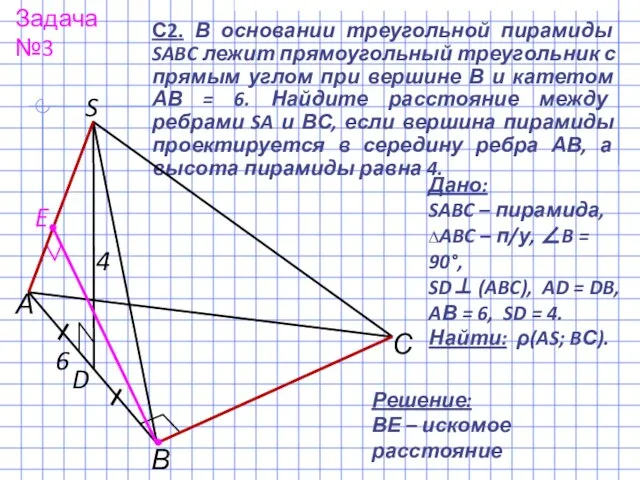
- 4. С2. В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине В и
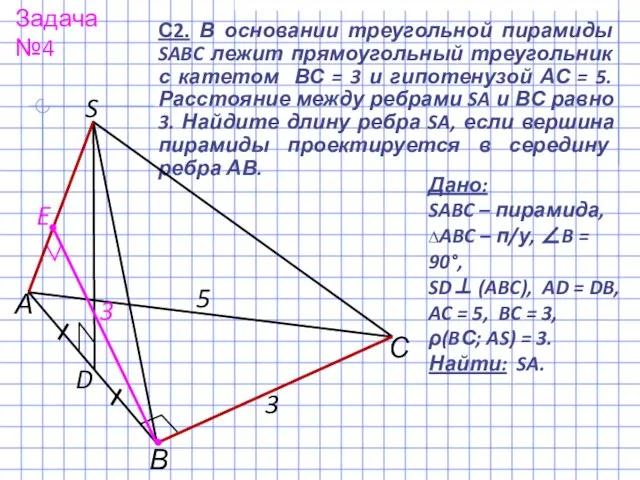
- 5. С2. В основании треугольной пирамиды SABC лежит прямоугольный треугольник с катетом ВС = 3 и гипотенузой
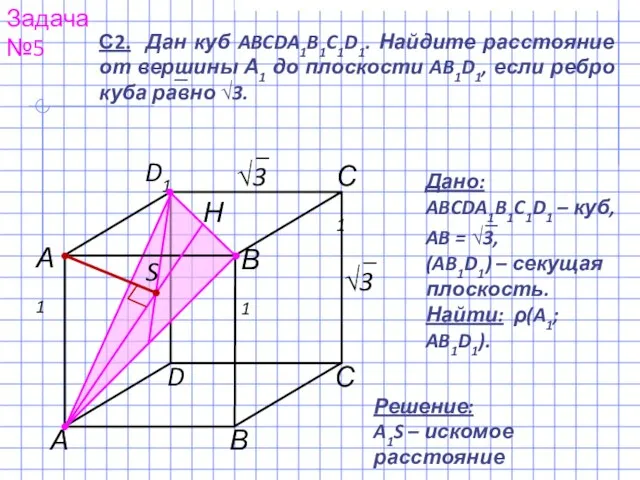
- 6. Задача №5 А С В D А1 С1 В1 D1 S Решение: A1S – искомое расстояние
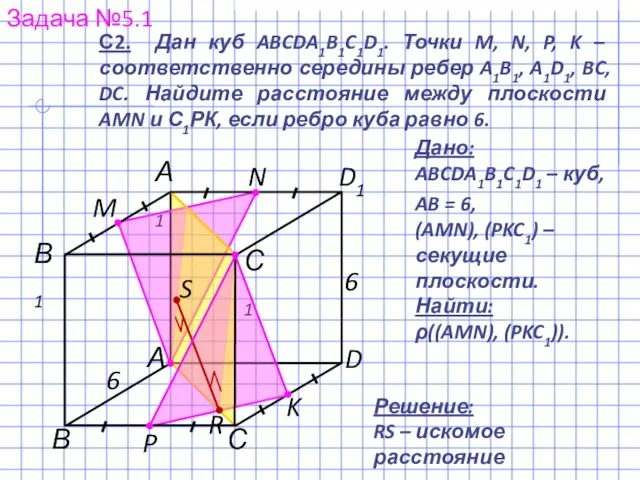
- 7. Задача №5.1 С В А1 С1 D1 С2. Дан куб ABCDA1B1C1D1. Точки M, N, P, K
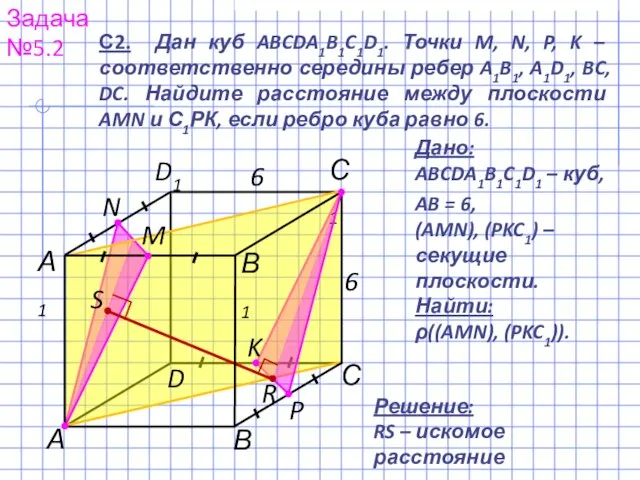
- 8. Задача №5.2 А С В А1 С1 D1 С2. Дан куб ABCDA1B1C1D1. Точки M, N, P,
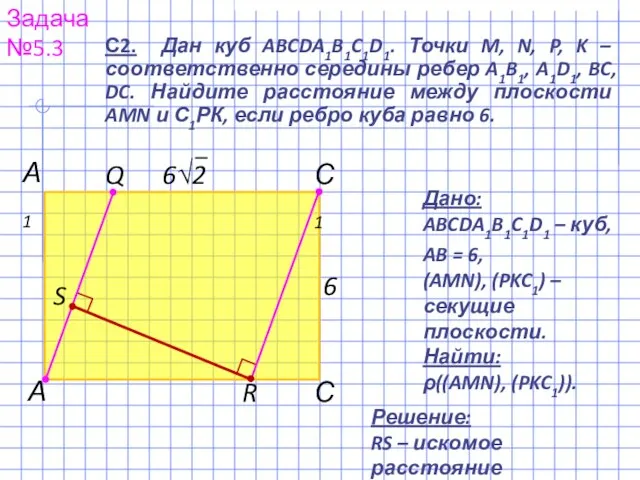
- 9. R Задача №5.3 А С А1 С1 С2. Дан куб ABCDA1B1C1D1. Точки M, N, P, K
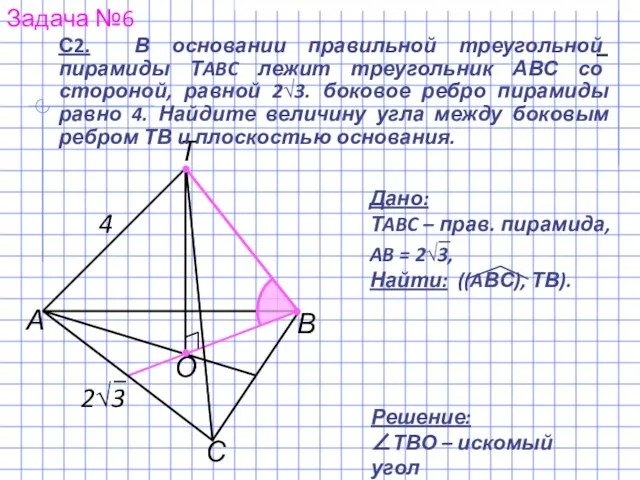
- 10. В Задача №6 А С Т Решение: ∠ТВО – искомый угол О 4
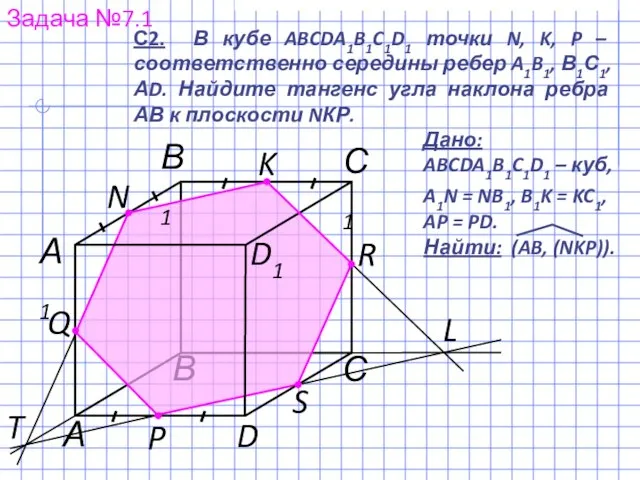
- 11. В S Задача №7.1 С А1 С1 D1 N P D В1 K А Q R
- 13. Скачать презентацию
 Числовые промежутки
Числовые промежутки  5 класс _
5 класс _ Масштаб
Масштаб Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Координатная плоскость
Координатная плоскость Функции комплексного переменного
Функции комплексного переменного Основные алгебраические структуры. (Глава 3)
Основные алгебраические структуры. (Глава 3) Определение производной от функции
Определение производной от функции Свойства логарифмов
Свойства логарифмов Треугольник
Треугольник Использование производной для исследования функций и построения графиков. 11 класс
Использование производной для исследования функций и построения графиков. 11 класс Измерение отрезков и углов
Измерение отрезков и углов Понятие булева вектора (двоичного вектора)
Понятие булева вектора (двоичного вектора) Координатная плоскость. Основные понятия
Координатная плоскость. Основные понятия Математика профильный уровень. Тест №11
Математика профильный уровень. Тест №11 Сложение и вычитание положительных и отрицательных чисел. (6 класс)
Сложение и вычитание положительных и отрицательных чисел. (6 класс) Сравнение арифметической и геометрической прогрессий (Алгебра 9 класс)
Сравнение арифметической и геометрической прогрессий (Алгебра 9 класс) Измерение высоты здания при помощи подобных треугольников
Измерение высоты здания при помощи подобных треугольников Интерактивный тренажёр. Состав чисел в пределах 10
Интерактивный тренажёр. Состав чисел в пределах 10 Площадь трапеции
Площадь трапеции Теория вероятностей
Теория вероятностей Десятичная система счисления
Десятичная система счисления Статистические наблюдения
Статистические наблюдения Основы комбинаторики. Размещения, перестановки, сочетания
Основы комбинаторики. Размещения, перестановки, сочетания Чтение свойств производной функции по графику этой функции
Чтение свойств производной функции по графику этой функции Координаты Подготовила и провела в 7 классе: Учитель математики и информатики Яковлева Н.С.
Координаты Подготовила и провела в 7 классе: Учитель математики и информатики Яковлева Н.С. Готовимся к Всероссийским проверочным работам по математике
Готовимся к Всероссийским проверочным работам по математике Вычитание дроби из целого числа
Вычитание дроби из целого числа