Содержание
- 2. Оглавление: 1) Общие сведения 2) Симметрия куба 3) Симметрия прямоугольного параллелепипеда 4) Симметрия параллелепипеда 5) Симметрия
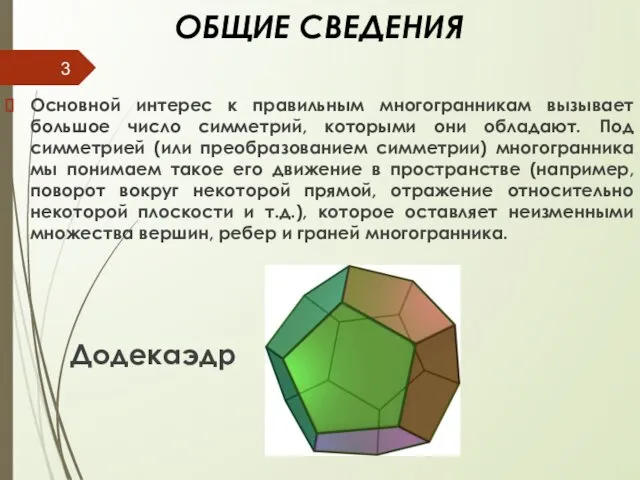
- 3. ОБЩИЕ СВЕДЕНИЯ Основной интерес к правильным многогранникам вызывает большое число симметрий, которыми они обладают. Под симметрией
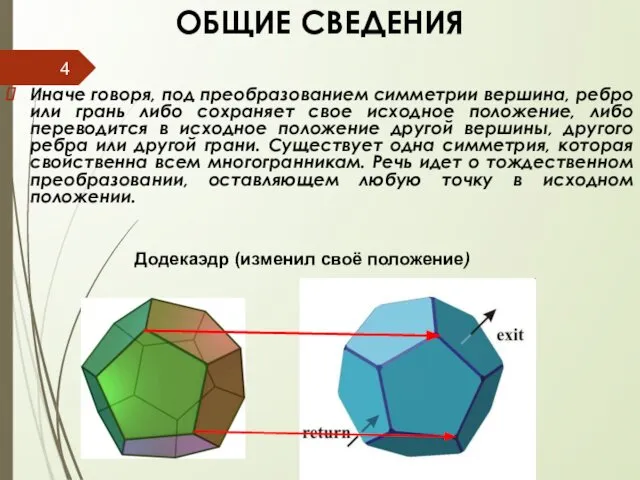
- 4. ОБЩИЕ CВЕДЕНИЯ Иначе говоря, под преобразованием симметрии вершина, ребро или грань либо сохраняет свое исходное положение,
- 5. ОБЩИЕ CВЕДЕНИЯ ПЛАТОНОВЫ ТЕЛА, или правильные многогранники, имеют в качестве граней правильные многоугольники, причем число граней,
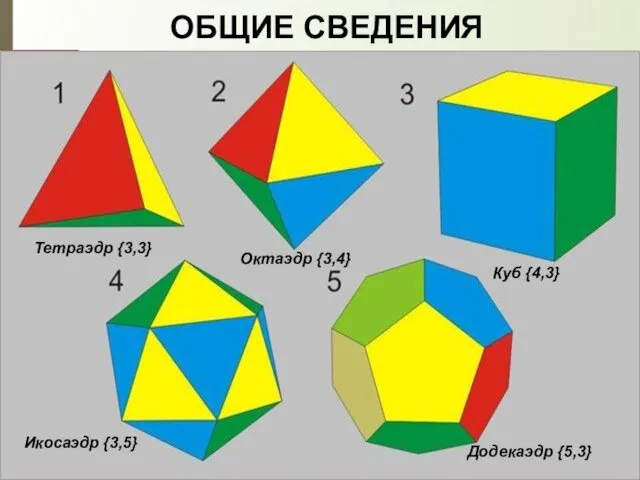
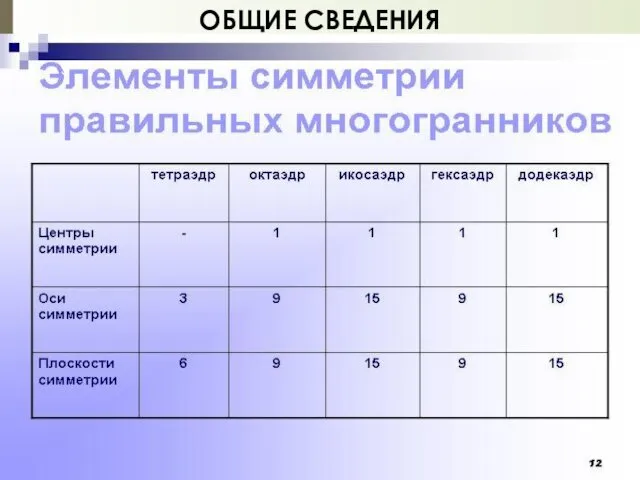
- 6. ОБЩИЕ СВЕДЕНИЯ Тетраэдр {3,3} Куб {4,3} Октаэдр {3,4} Икосаэдр {3,5} Додекаэдр {5,3}
- 7. ОБЩИЕ СВЕДЕНИЯ С самым распространенным примером симметрии мы встречаемся в случае прямой правильной n-угольной призмы. Пусть
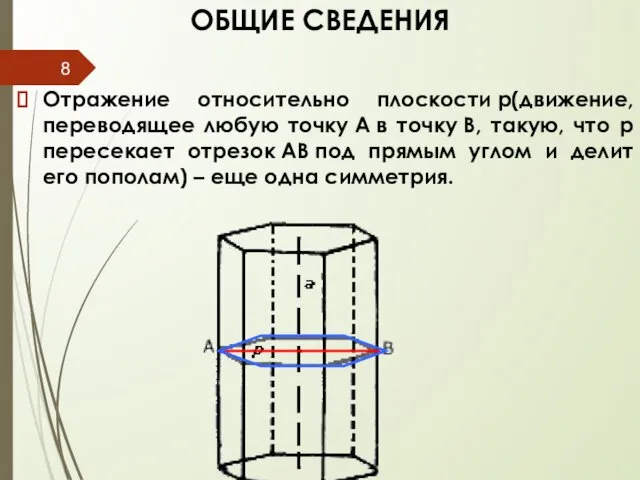
- 8. ОБЩИЕ СВЕДЕНИЯ Отражение относительно плоскости p(движение, переводящее любую точку A в точку B, такую, что p
- 9. ОБЩИЕ СВЕДЕНИЯ
- 10. ОБЩИЕ СВЕДЕНИЯ Любую симметрию многогранника можно представить в виде произведения отражений. Под произведением нескольких движений многогранника
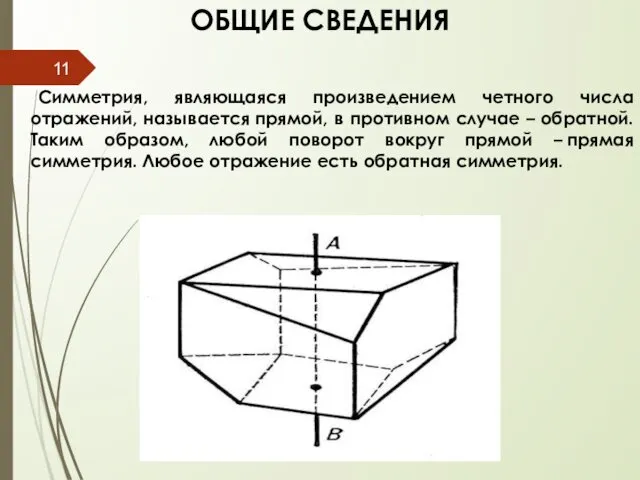
- 11. ОБЩИЕ СВЕДЕНИЯ Симметрия, являющаяся произведением четного числа отражений, называется прямой, в противном случае – обратной. Таким
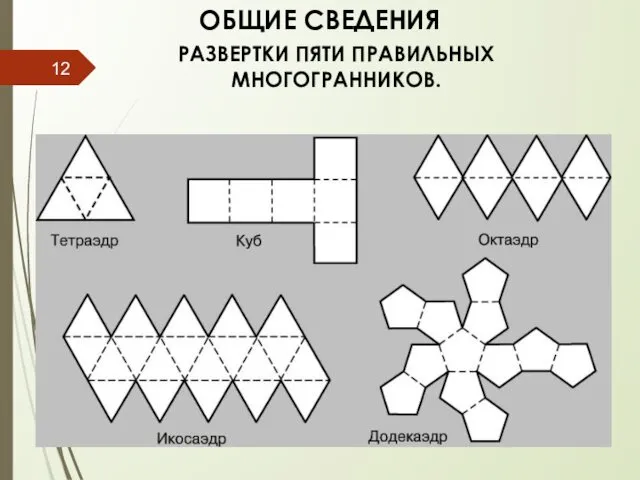
- 12. РАЗВЕРТКИ ПЯТИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ. ОБЩИЕ СВЕДЕНИЯ
- 13. ОБЩИЕ СВЕДЕНИЯ Рассмотрим подробнее симметрии тетраэдра, т.е. правильного многогранника. Любая прямая, проходящая через любую вершину и
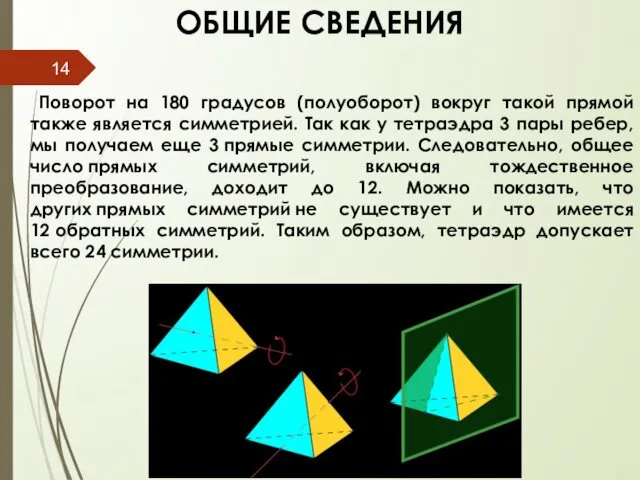
- 14. ОБЩИЕ СВЕДЕНИЯ Поворот на 180 градусов (полуоборот) вокруг такой прямой также является симметрией. Так как у
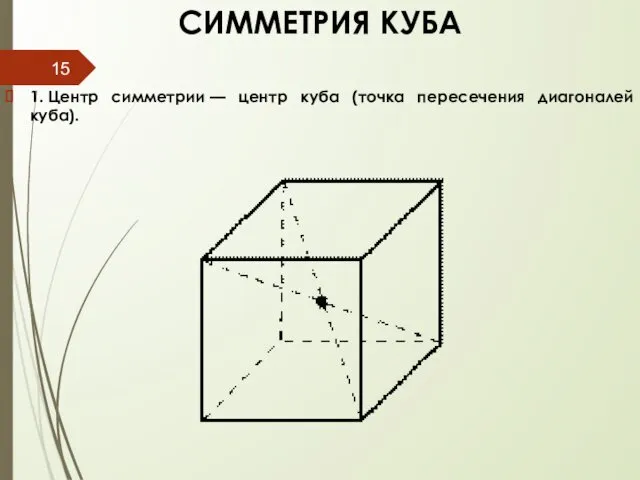
- 15. СИММЕТРИЯ КУБА 1. Центр симметрии — центр куба (точка пересечения диагоналей куба).
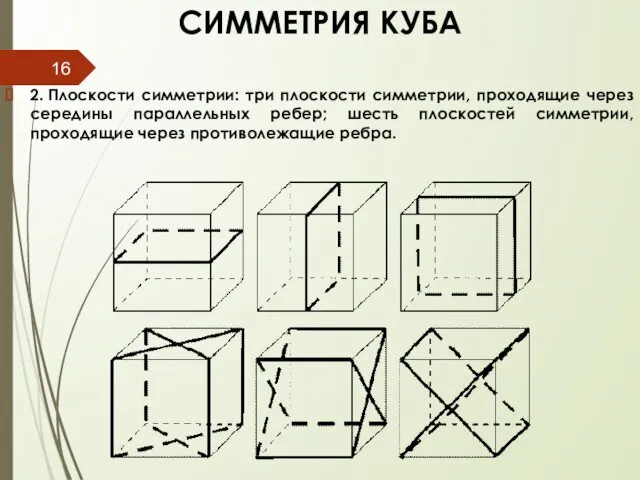
- 16. СИММЕТРИЯ КУБА 2. Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер; шесть плоскостей симметрии,
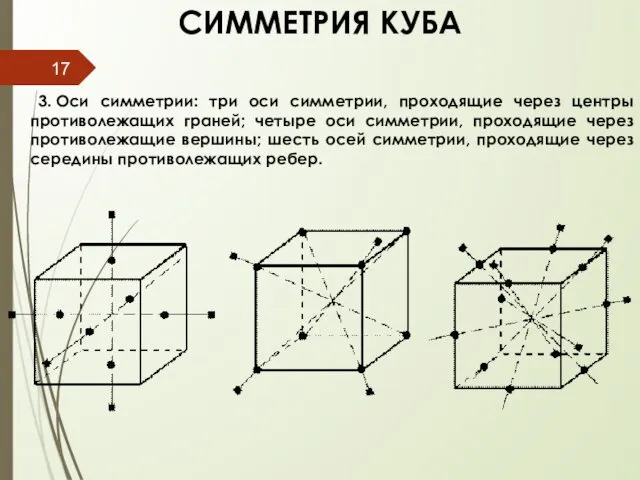
- 17. СИММЕТРИЯ КУБА 3. Оси симметрии: три оси симметрии, проходящие через центры противолежащих граней; четыре оси симметрии,
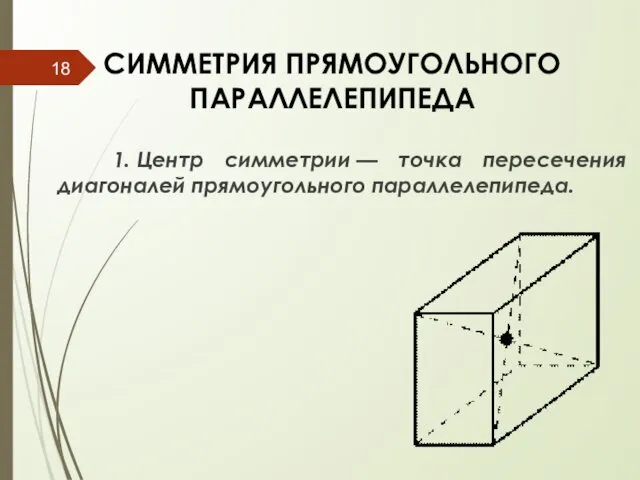
- 18. СИММЕТРИЯ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА 1. Центр симметрии — точка пересечения диагоналей прямоугольного параллелепипеда.
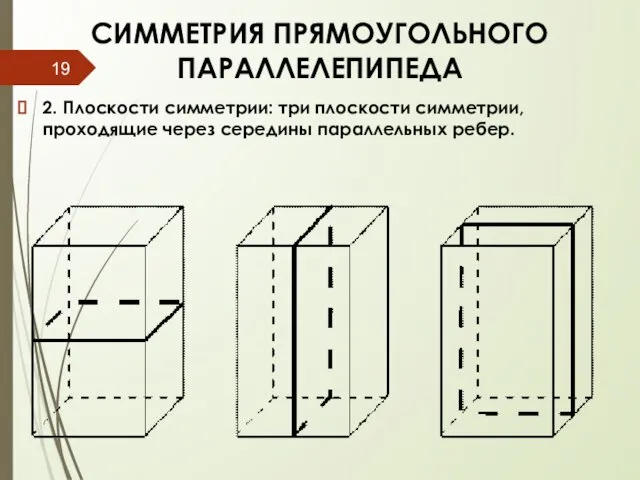
- 19. СИММЕТРИЯ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА 2. Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер.
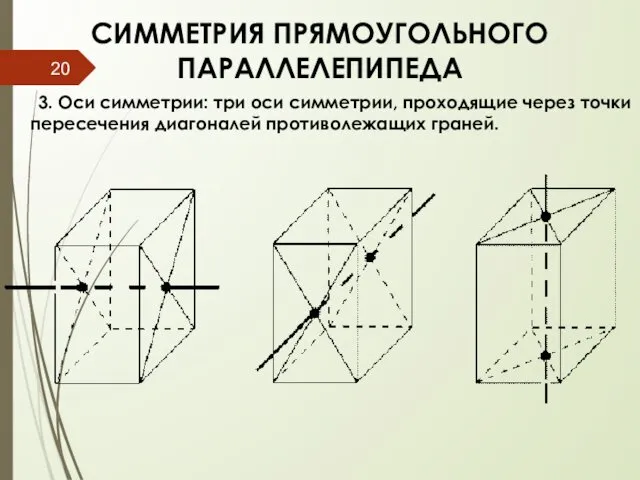
- 20. СИММЕТРИЯ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА 3. Оси симметрии: три оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней.
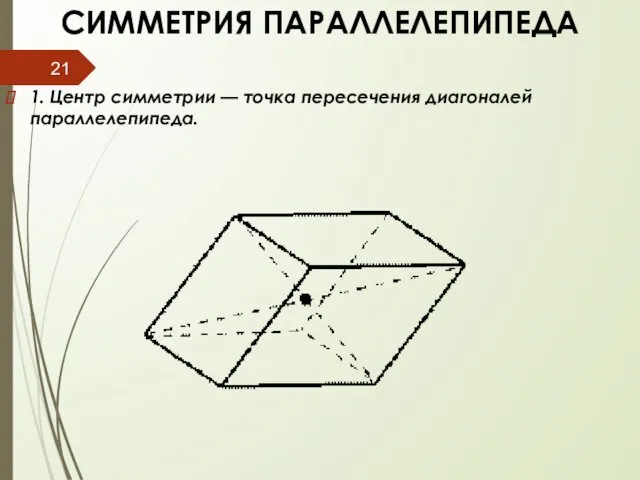
- 21. СИММЕТРИЯ ПАРАЛЛЕЛЕПИПЕДА 1. Центр симметрии — точка пересечения диагоналей параллелепипеда.
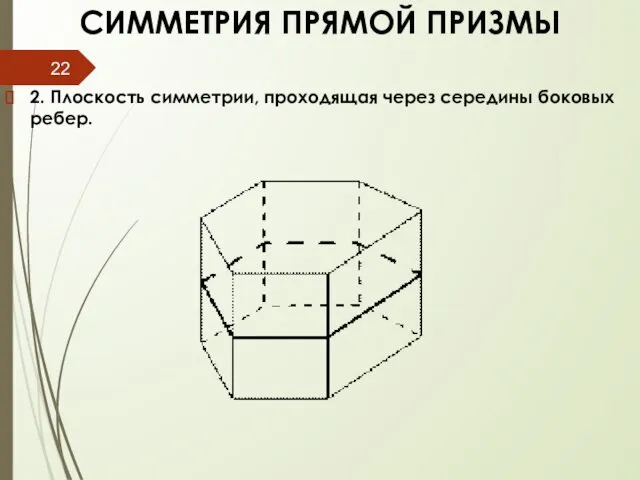
- 22. СИММЕТРИЯ ПРЯМОЙ ПРИЗМЫ 2. Плоскость симметрии, проходящая через середины боковых ребер.
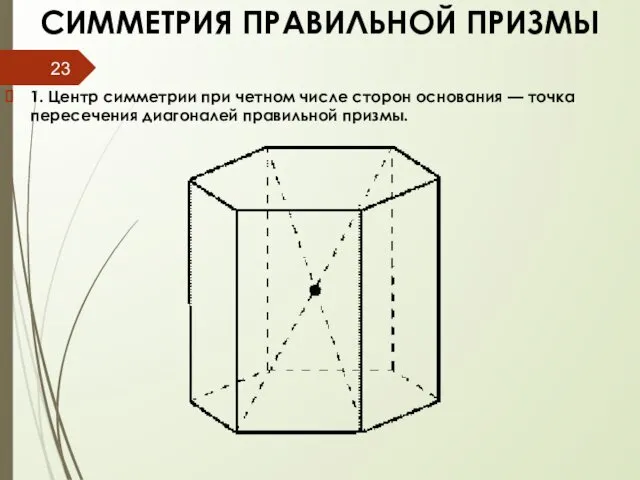
- 23. СИММЕТРИЯ ПРАВИЛЬНОЙ ПРИЗМЫ 1. Центр симметрии при четном числе сторон основания — точка пересечения диагоналей правильной
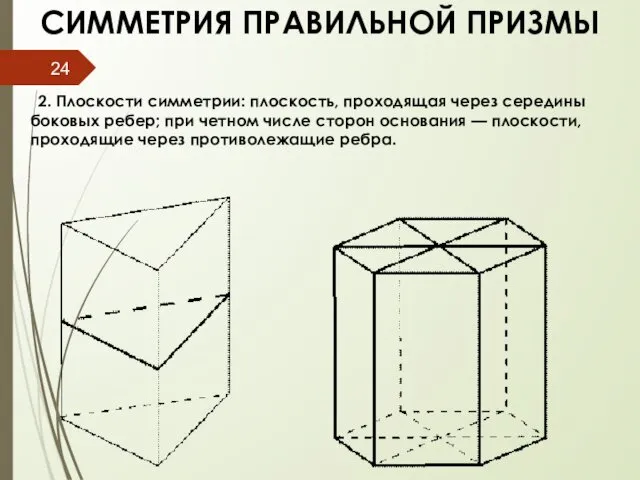
- 24. СИММЕТРИЯ ПРАВИЛЬНОЙ ПРИЗМЫ 2. Плоскости симметрии: плоскость, проходящая через середины боковых ребер; при четном числе сторон
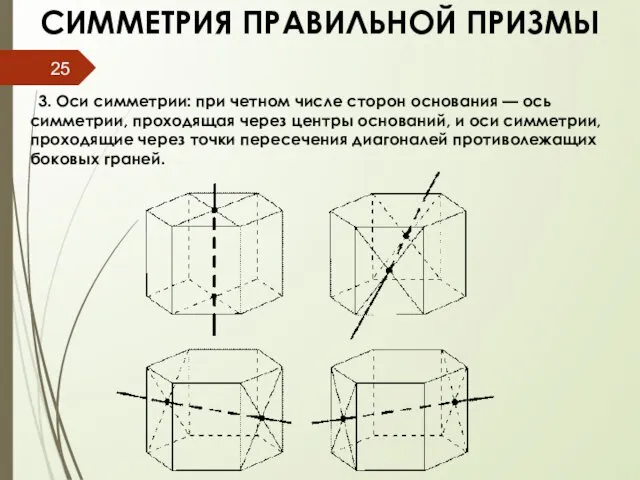
- 25. СИММЕТРИЯ ПРАВИЛЬНОЙ ПРИЗМЫ 3. Оси симметрии: при четном числе сторон основания — ось симметрии, проходящая через
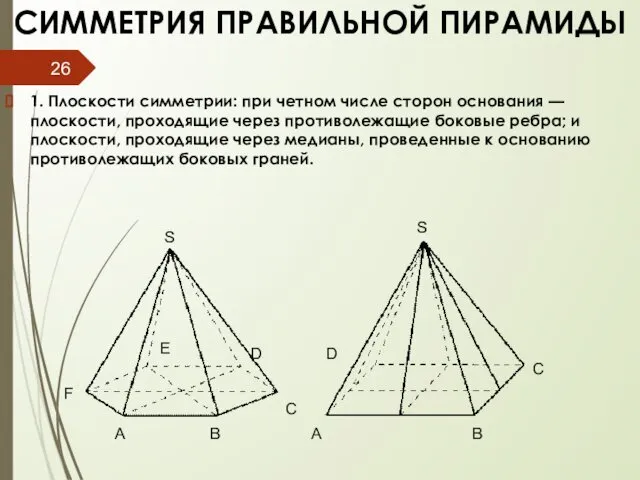
- 26. СИММЕТРИЯ ПРАВИЛЬНОЙ ПИРАМИДЫ 1. Плоскости симметрии: при четном числе сторон основания — плоскости, проходящие через противолежащие
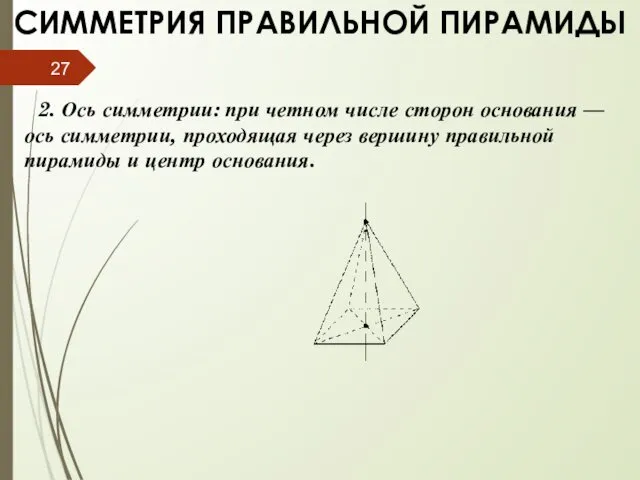
- 27. СИММЕТРИЯ ПРАВИЛЬНОЙ ПИРАМИДЫ 2. Ось симметрии: при четном числе сторон основания — ось симметрии, проходящая через
- 29. Скачать презентацию





 Координатная плоскость (урок 1)
Координатная плоскость (урок 1) Объем тела, ограниченного поверхностями. (Лекция 2.2)
Объем тела, ограниченного поверхностями. (Лекция 2.2) Занимательная математика
Занимательная математика Постановка задачи оптимизации (основные этапы и пример)
Постановка задачи оптимизации (основные этапы и пример) Презентация по математике "Разложение на множители суммы и разности кубов" - скачать
Презентация по математике "Разложение на множители суммы и разности кубов" - скачать  Площадь криволинейной трапеции
Площадь криволинейной трапеции Как «устроены» числа.
Как «устроены» числа. Производные элементарных функций
Производные элементарных функций В королевстве десятичных дробей
В королевстве десятичных дробей Арифметическая и геометрическая прогрессия
Арифметическая и геометрическая прогрессия Неравенства с модулем
Неравенства с модулем Матрицы. Основные понятия
Матрицы. Основные понятия Основные формулы комбинаторики
Основные формулы комбинаторики Презентация по математике "Расчет пути и времени движения" - скачать бесплатно
Презентация по математике "Расчет пути и времени движения" - скачать бесплатно Смешанные числа Презентация выполнена учителем математики Ивановской СОШ Иваненко ОВ_
Смешанные числа Презентация выполнена учителем математики Ивановской СОШ Иваненко ОВ_ «Действия с натуральными числами» Урок – игра «Крестики-нолики» 5 класс Учитель: Ниязова Н.Г.
«Действия с натуральными числами» Урок – игра «Крестики-нолики» 5 класс Учитель: Ниязова Н.Г. Дүртпочмаклар. Кайсы фигура артык
Дүртпочмаклар. Кайсы фигура артык Основные свойства степеней
Основные свойства степеней Графики функций и их свойства
Графики функций и их свойства Размерность. Единицы измерения
Размерность. Единицы измерения Деление одночлена на одночлен. Урок 50. 7 класс
Деление одночлена на одночлен. Урок 50. 7 класс Презентация по математике "Золотое сечение на Новгородчине" - скачать
Презентация по математике "Золотое сечение на Новгородчине" - скачать  Гетероскедастичность. Предпосылки МНК, связанные с ошибками
Гетероскедастичность. Предпосылки МНК, связанные с ошибками Решение заданий №8. Пирамида. По материалам открытого банка задач ЕГЭ
Решение заданий №8. Пирамида. По материалам открытого банка задач ЕГЭ Задачи на построение с помощью циркуля и линейки
Задачи на построение с помощью циркуля и линейки Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Рациональные выражения. Урок 1-2
Рациональные выражения. Урок 1-2 Проценты каждый день!
Проценты каждый день!