Содержание
- 2. Chapter Three: Numerical Measures of the Data Outline Introduction 3-1 Measures of Central Tendency 3-2 Measures
- 3. Chapter Three: Numerical Measures of the Data Objectives Summarize data using the measures of central tendency,
- 4. Chapter Three: Numerical Measures of the Data 3-1 Measures of Central tendency We will compute two
- 5. Chapter Three: Numerical Measures of the Data Example:- (Sample Mean) The ages of a random sample
- 6. Chapter Three: Numerical Measures of the Data Example:- population mean Statistics103110 3-
- 7. Chapter Three: Numerical Measures of the Data The Sample Mean for an Ungrouped Frequency Distribution Statistics103110
- 8. Chapter Three: Numerical Measures of the Data The Sample Mean for an Ungrouped Frequency Distribution –
- 9. Chapter Three: Numerical Measures of the Data The Sample Mean for a Grouped Frequency Distribution The
- 10. Important remark : In some situations the mean may not be representative of the data. As
- 11. Properties of the mean As stated, the mean is a widely used measure of central tendency
- 12. Chapter Three: Numerical Measures of the Data Median : The median splits the ordered data into
- 13. Chapter Three: Numerical Measures of the Data When there is an even number of values in
- 14. example Find the median grade of the following sample of students grades : A B A
- 15. Properties of the Median The major properties of the median are: The median is a unique
- 16. Chapter Three: Numerical Measures of the Data Mode:- is the score that occurs most frequently (denoted
- 17. Chapter Three: Numerical Measures of the Data Example:- Eleven different automobiles were tested at a speed
- 18. Chapter Three: Numerical Measures of the Data The Mode for a Grouped Frequency Distribution – Can
- 19. Properties of the Mode The mode can be found for all levels of data (nominal, ordinal,
- 20. Chapter Three: Numerical Measures of the Data The weighted mean is used when the values in
- 21. Chapter Three: Numerical Measures of the Data Example:- During a one hour period on a hot
- 22. Best measure of central tendency
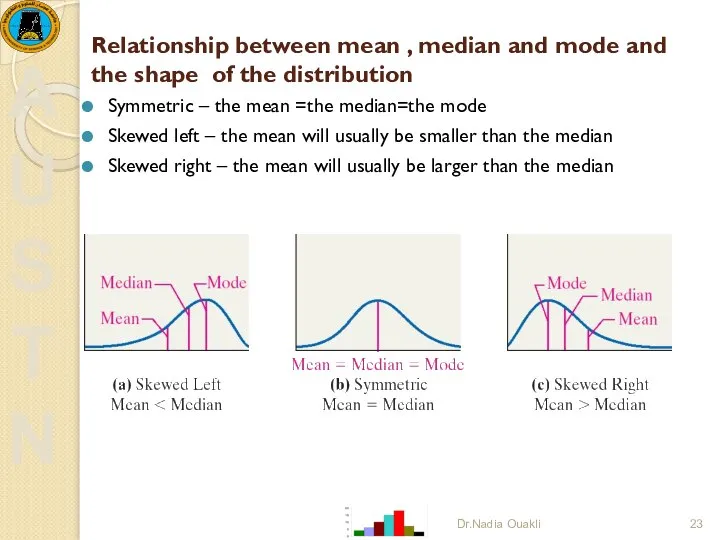
- 23. Relationship between mean , median and mode and the shape of the distribution Symmetric – the
- 24. Chapter Three: Numerical Measures of the Data 3-2 Measures of Dispersion( variation) o the spread or
- 25. Variability -- provides a quantitative measure of the degree to which scores in a distribution are
- 26. Measures of dispersion are : The range , The interquartile range , The variance and standard
- 27. Example Compute the range of 6, 1, 2, 6, 11, 7, 3, 3 The largest value
- 28. The variance of a variable The variance is based on the deviation from the mean (
- 29. Chapter Three: Numerical Measures of the Data The population variance of a variable is the sum
- 30. Properties of the variance and standard deviation it is the typical or approx. average distance from
- 31. Chapter Three: Numerical Measures of the Data The sample variance of a variable is the sum
- 32. Symbols for Standard Deviation Sample Population σ σ x xσn Book Some graphics calculators Some non-graphics
- 33. Chapter Three: Numerical Measures of the Data Sample Variance for Grouped and Ungrouped Data For grouped
- 34. Step one put the data I ungrouped frequency table Chapter Three: Numerical Measures of the Data
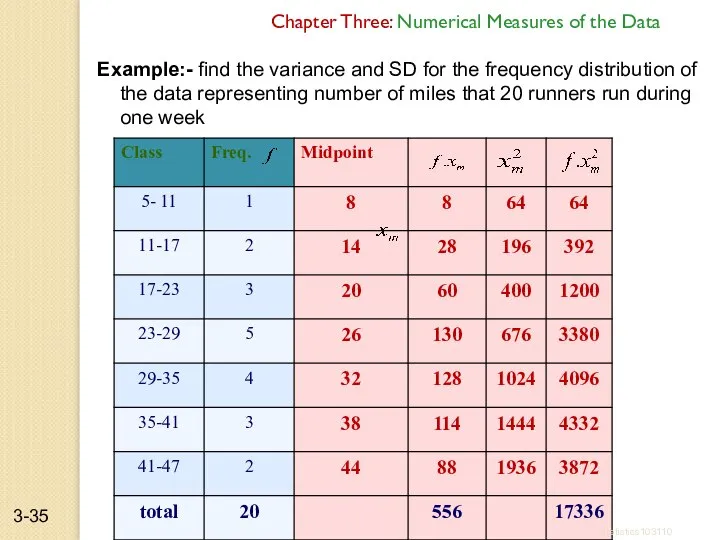
- 35. Example:- find the variance and SD for the frequency distribution of the data representing number of
- 36. Chapter Three: Numerical Measures of the Data Statistics103110 3-
- 37. Chapter Three: Numerical Measures of the Data Interpretation and Uses of the Standard Deviation The standard
- 38. Chapter Three: Numerical Measures of the Data Coefficient of Variation :- The relative measure of St.
- 39. Example : To see why the coefficient of variation should not be applied to interval level
- 40. Advantages The coefficient of variation is useful because the standard deviation of data must always be
- 41. Example:- Data about the annual salary (000’s) and age of CEO’s in a number of firms
- 42. Chapter Three: Numerical Measures of the Data Measure of position: Measures of position are used to
- 43. Chapter Three: Numerical Measures of the Data Standard Scores (or z-scores) specify the exact location of
- 44. Chapter Three: Numerical Measures of the Data Characteristics of Standard Scores The shape of the distribution
- 45. Chapter Three: Numerical Measures of the Data Example:- A student scored 65 on a statistics exam
- 46. Example:- a student scored 65 on a calculus test that had a mean of 50 and
- 47. Chapter Three: Numerical Measures of the Data Quartiles divide the data set into 4 groups. Quartiles
- 48. Chapter Three: Numerical Measures of the Data Example: For the following data set: 2, 3, 5,
- 49. Chapter Three: Numerical Measures of the Data Example: Find Q1 and Q3 for the following data
- 50. Chapter Three: Numerical Measures of the Data Example: For the following data set: 2, 3, 5,
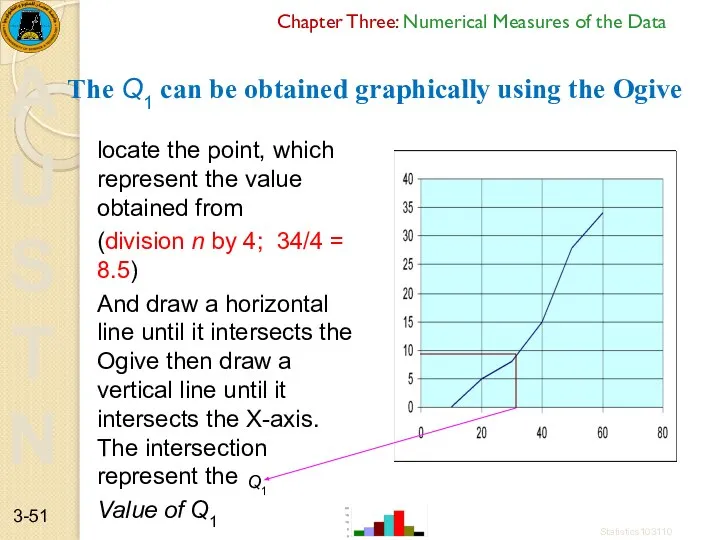
- 51. Chapter Three: Numerical Measures of the Data The Q1 can be obtained graphically using the Ogive
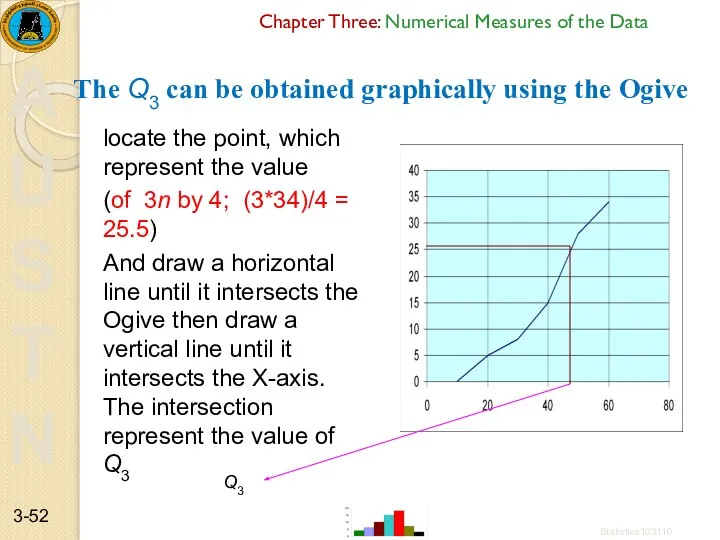
- 52. Chapter Three: Numerical Measures of the Data The Q3 can be obtained graphically using the Ogive
- 53. Chapter Three: Numerical Measures of the Data The Interquartile Range (IQR) The Interquartile Range, IQR =
- 54. Chapter Three: Numerical Measures of the Data An outlier is an extremely high or an extremely
- 55. Example Given the data set 5, 6, 12, 13, 15, 18, 22, 50, can the value
- 56. Chapter Three: Numerical Measures of the Data Measure of Dispersion tells us about the variation of
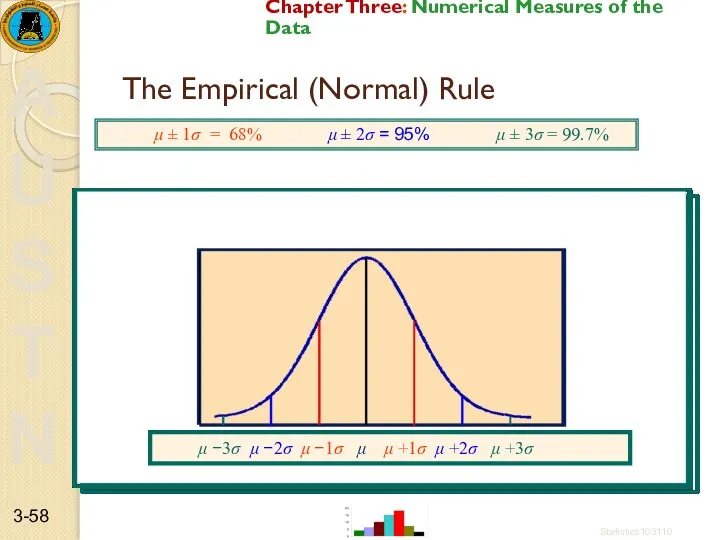
- 57. Chapter Three: Numerical Measures of the Data For any bell shaped distribution: Approximately 68% of the
- 58. The Empirical (Normal) Rule μ ± 1σ = 68% μ ± 2σ = 95% μ ±
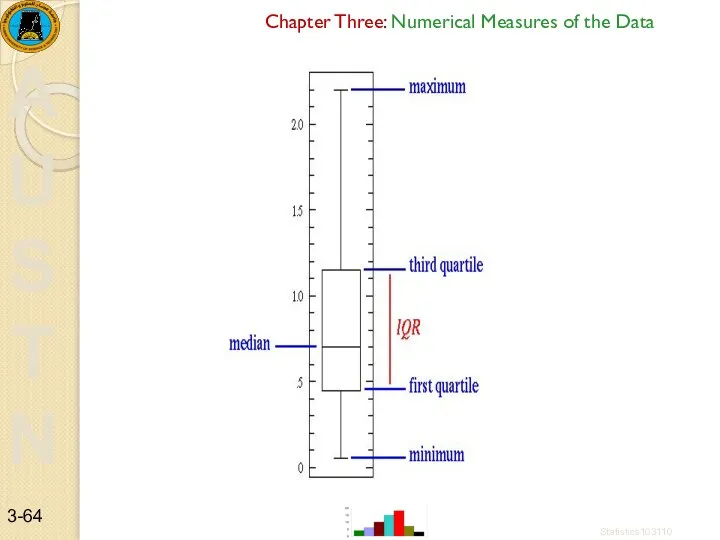
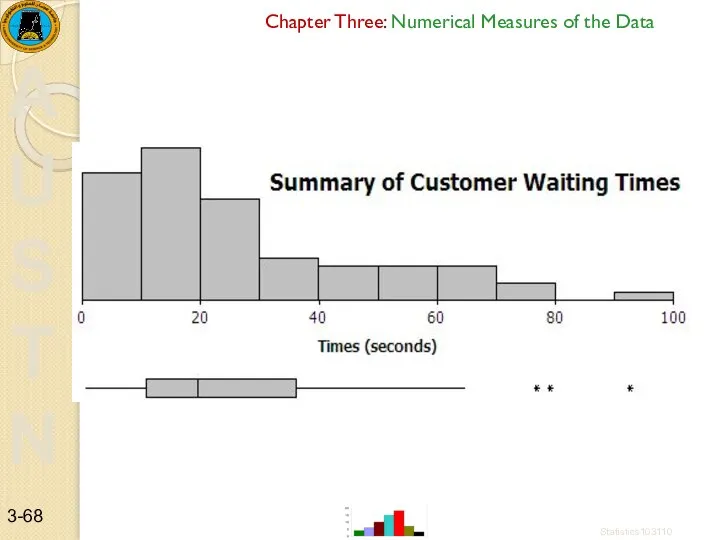
- 59. Chapter Three: Numerical Measures of the Data What is a Box Plot To construct a box
- 60. The box plot is useful in analyzing small data sets that do not lend themselves easily
- 61. How to use it: Collect and arrange data. Collect the data and arrange it into an
- 62. Obtain the minimum. This value will be the smallest data value that is greater than or
- 63. Example 1:- Failure times of industrial machines (in hours) 32.56 42.02 47.26 50.25 59.03 60.17 61.56
- 64. Chapter Three: Numerical Measures of the Data Statistics103110 3-
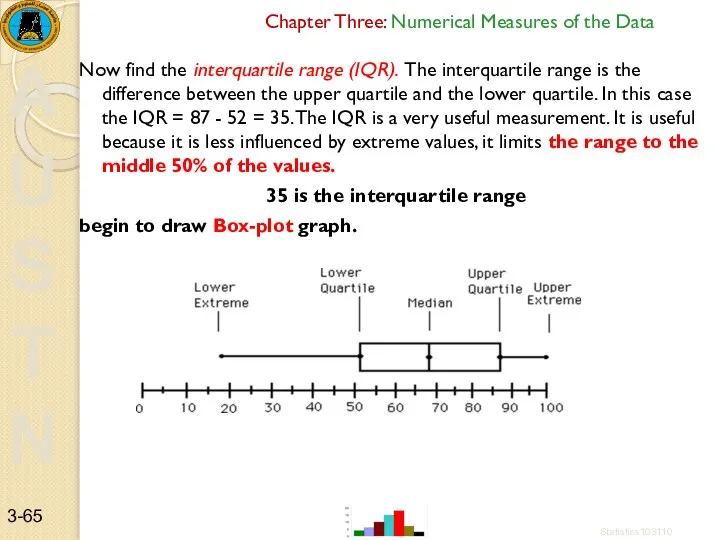
- 65. Chapter Three: Numerical Measures of the Data Now find the interquartile range (IQR). The interquartile range
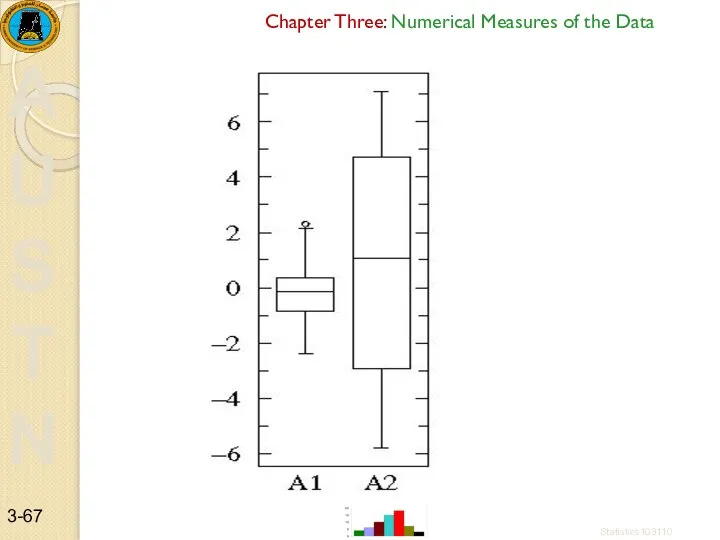
- 66. Chapter Three: Numerical Measures of the Data Example 2 Consider two datasets: A1={0.22, -0.87, -2.39, -1.79,
- 67. Chapter Three: Numerical Measures of the Data Statistics103110 3-
- 68. Chapter Three: Numerical Measures of the Data Statistics103110 3-
- 70. Скачать презентацию


























































 Величины и их измерение. (Тема 4)
Величины и их измерение. (Тема 4) Число и цифра 4
Число и цифра 4 Аттестационная работа. Организация познавательной деятельности на уроках математики в 5 классе
Аттестационная работа. Организация познавательной деятельности на уроках математики в 5 классе Статистические критерии различий (3). Критерии различий. Сравнение более двух выборок
Статистические критерии различий (3). Критерии различий. Сравнение более двух выборок Презентация по математике "Теория бесконечных множеств. Часть 2" - скачать бесплатно
Презентация по математике "Теория бесконечных множеств. Часть 2" - скачать бесплатно Что? Где? Когда? Математическая игра
Что? Где? Когда? Математическая игра Подготовка к контр работе. Решение задач по теме: площади. Теорема Пифагора.(первый урок)
Подготовка к контр работе. Решение задач по теме: площади. Теорема Пифагора.(первый урок) Таблица умножения. Тренажер
Таблица умножения. Тренажер Сумма углов в треугольнике
Сумма углов в треугольнике Основы математического моделирования
Основы математического моделирования Умножение и деление положительных и отрицательных чисел. Урок 48
Умножение и деление положительных и отрицательных чисел. Урок 48 Презентация по математике "Системы счисления. Задачи" - скачать
Презентация по математике "Системы счисления. Задачи" - скачать  Формулы. Решение задач
Формулы. Решение задач Единицы массы: грамм, килограмм
Единицы массы: грамм, килограмм Презентация по математике "Координаты на поле" - скачать
Презентация по математике "Координаты на поле" - скачать  Открытый урок в 10 «В» классе на тему: «Тригонометрические уравнения»
Открытый урок в 10 «В» классе на тему: «Тригонометрические уравнения» Анықталмағандықтар. Лопиталь ережес
Анықталмағандықтар. Лопиталь ережес Применение производной к исследованию функций
Применение производной к исследованию функций Дифференциальное исчисление функций нескольких переменных
Дифференциальное исчисление функций нескольких переменных Задачи на построение
Задачи на построение Интерактивные тренинги по математике для подготовки к ЕГЭ
Интерактивные тренинги по математике для подготовки к ЕГЭ Подготовка к контрольной работе №5. Свойства прямоугольного треугольника
Подготовка к контрольной работе №5. Свойства прямоугольного треугольника Связь между суммой и слагаемыми
Связь между суммой и слагаемыми Модели статистического прогнозирования (11класс)
Модели статистического прогнозирования (11класс) Процент төшенчәсе белән танышу. Процентлар табу
Процент төшенчәсе белән танышу. Процентлар табу Расстояние от точки до плоскости. Теорема о трех перпендикулярах
Расстояние от точки до плоскости. Теорема о трех перпендикулярах Квадратичная функция, её свойства и график
Квадратичная функция, её свойства и график Теорема Пифагора
Теорема Пифагора