Содержание
- 2. 2.3.2. Моделирование процедур оценивание параметров состояния стохастических динамических систем в непрерывном времени Постановка задачи: для применения
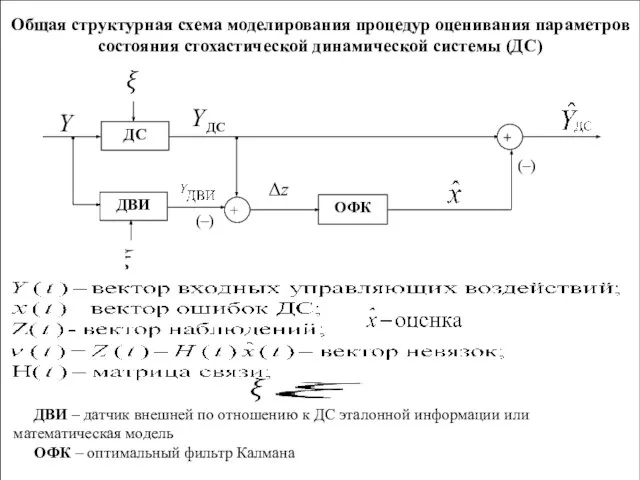
- 3. Общая структурная схема моделирования процедур оценивания параметров состояния стохастической динамической системы (ДС) ДС + (–) ДВИ
- 4. Оптимальные оценки вектора ошибок ДС могут быть найдены по наблюдениям . На практике в качестве критерия
- 5. (2.30) где Подставляя выражение для в соотношение (2.30) и учитывая, что , получим (2.31) Теперь коэффициент
- 6. (2.32) Уравнение (2.32) превращается в тождество, если Отсюда оптимальный коэффициент усиления будет иметь вид Подставляя найденный
- 8. Скачать презентацию




 Весёлые человечки спешат на помощь. Занятие для дошкольников
Весёлые человечки спешат на помощь. Занятие для дошкольников Геометрическая прогрессия
Геометрическая прогрессия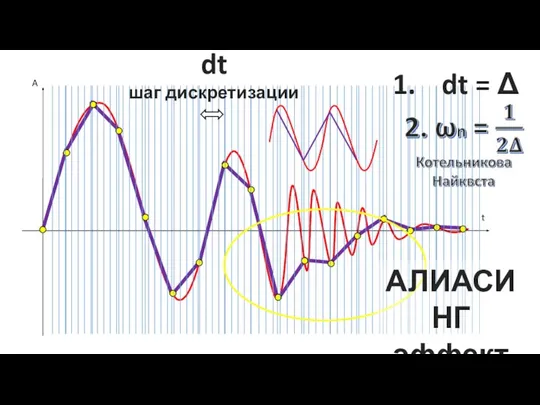 Алиасинг эффект. АЦП σ-δ. Интегратор
Алиасинг эффект. АЦП σ-δ. Интегратор მენეჯერული სტატისტიკა. შერჩევა და შერჩევის განაწილება. თავი 7
მენეჯერული სტატისტიკა. შერჩევა და შერჩევის განაწილება. თავი 7 Математико-статистическое методы в педагогических исследованиях
Математико-статистическое методы в педагогических исследованиях Системы счисления. (Тема 2)
Системы счисления. (Тема 2) Презентация на тему Площадь трапеции
Презентация на тему Площадь трапеции  Інтерполяційні методи наближення функцій двох змінних
Інтерполяційні методи наближення функцій двох змінних Начальные сведения из геометрии
Начальные сведения из геометрии Староисаковская средняя общеобразовательная школа Бугульминского муниципального района Конспект – презентация урока « ЗОЖ
Староисаковская средняя общеобразовательная школа Бугульминского муниципального района Конспект – презентация урока « ЗОЖ Системы линейных уравнений
Системы линейных уравнений Математическая логика
Математическая логика Измерение высоты здания булавочным способом
Измерение высоты здания булавочным способом Сызықтық жұп регрессия теңдеуі
Сызықтық жұп регрессия теңдеуі Хроника развития тригонометрии
Хроника развития тригонометрии Математический анализ
Математический анализ Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел Розв’язування логарифмічних рівнянь
Розв’язування логарифмічних рівнянь Презентация по математике "Играем в прятки с овощами" - скачать
Презентация по математике "Играем в прятки с овощами" - скачать  Логарифмическая функция, ее свойства и график
Логарифмическая функция, ее свойства и график Решение тестовых заданий по математике. Подготовка к ГИА
Решение тестовых заданий по математике. Подготовка к ГИА Функції багатьох змінних
Функції багатьох змінних Численность населения города Кингисепп и Кингисеппского района в различные периоды времени.(4 класс)
Численность населения города Кингисепп и Кингисеппского района в различные периоды времени.(4 класс) Тема урока «Вычисление производных» Подготовил: учитель физики и математики Гребенщикова А.Г. ГОУ ТО «Тульская специальная (ко
Тема урока «Вычисление производных» Подготовил: учитель физики и математики Гребенщикова А.Г. ГОУ ТО «Тульская специальная (ко Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ
Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ Иоганн Карл Август Радон (1887-1956). Преобразование Радона
Иоганн Карл Август Радон (1887-1956). Преобразование Радона Программно-аппаратный комплекс для автоматизации управленческой деятельности школы
Программно-аппаратный комплекс для автоматизации управленческой деятельности школы Параллельные прямые. Признаки параллельности прямых
Параллельные прямые. Признаки параллельности прямых