Содержание
- 2. Ключевые понятия к данной теме: ─ подграф графа; ─ пустой граф (подграф); ─ полный граф (подграф).
- 3. Постановка задачи
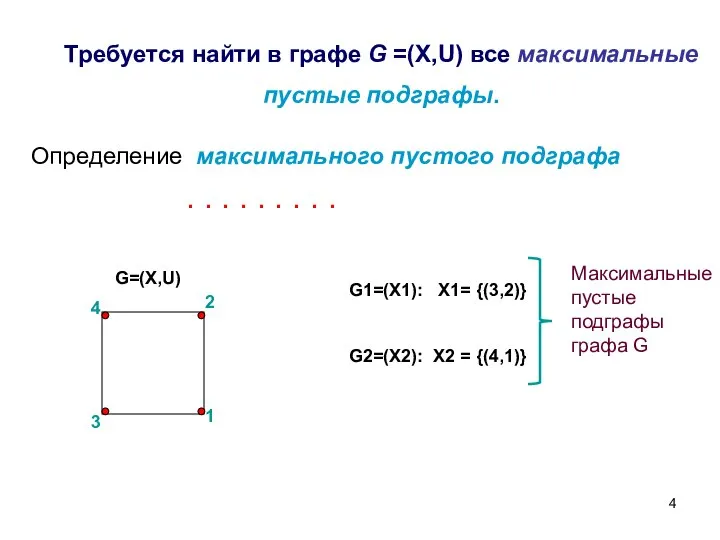
- 4. Требуется найти в графе G =(X,U) все максимальные пустые подграфы. Определение максимального пустого подграфа G1=(X1): X1=
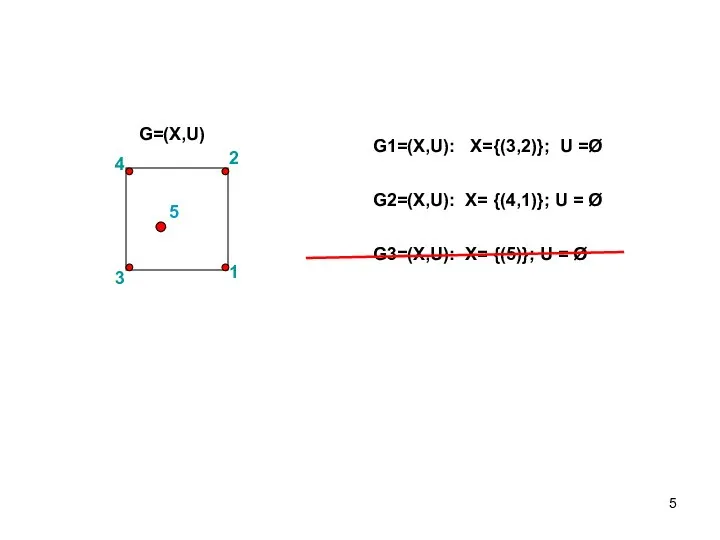
- 5. G1=(X,U): X={(3,2)}; U =Ø G2=(X,U): X= {(4,1)}; U = Ø G3=(X,U): X= {(5)}; U = Ø
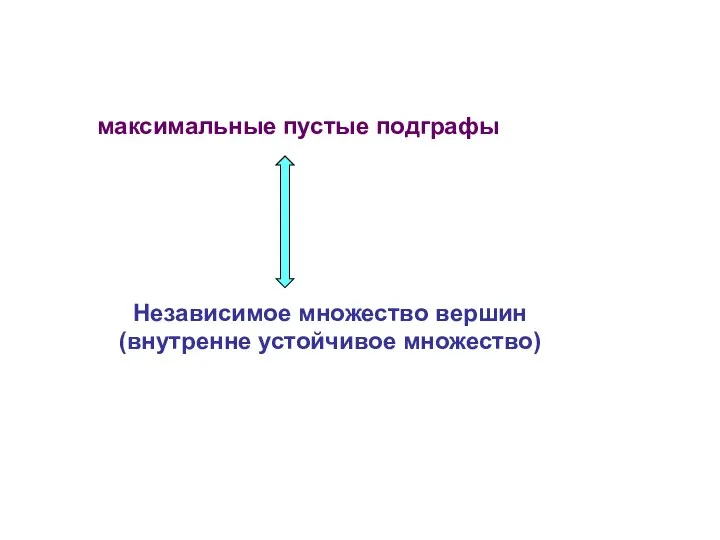
- 6. Независимое множество вершин (внутренне устойчивое множество) максимальные пустые подграфы
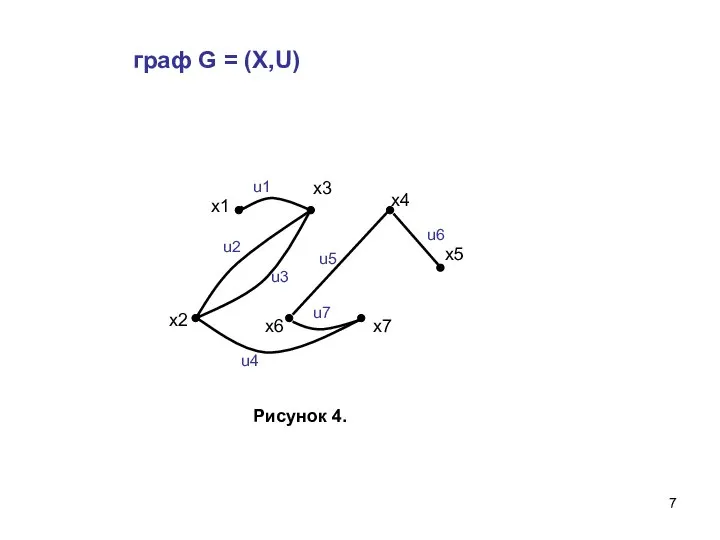
- 7. граф G = (X,U)
- 8. нахождения в графе G всех максимальных пустых подграфов Рассмотрим алгоритм Х.Магу, Дж.Уэйсмана
- 9. Законы алгебры логики Эквивалентные преобразования f = x1v x2 f = x1x2 v x1x2 f =
- 10. (a+b) (a+c)… (a+p)= a+bc…p x v xy = x операция поглощения операция склеивания x(x y) =
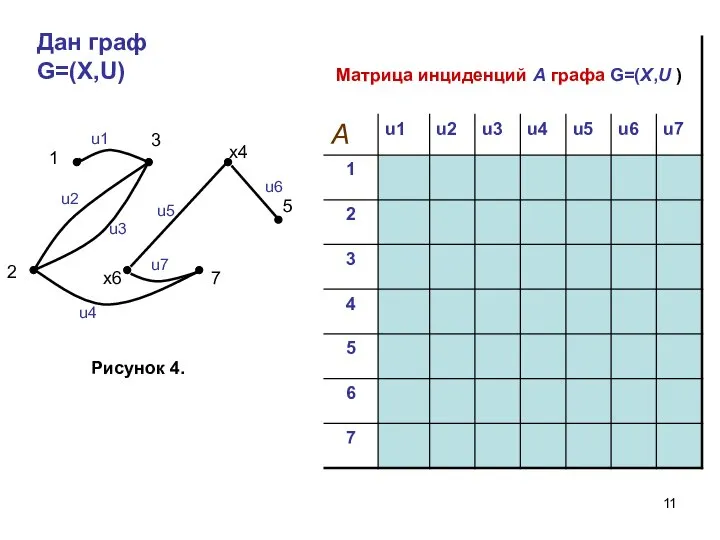
- 11. Дан граф G=(X,U)
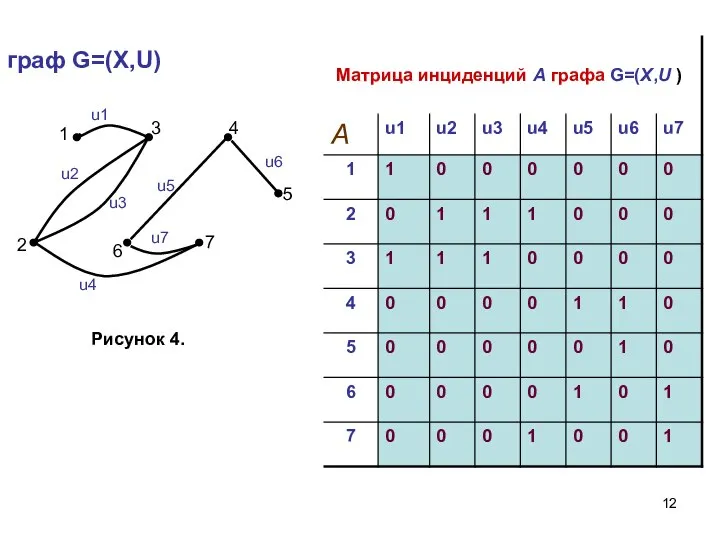
- 12. граф G=(X,U)
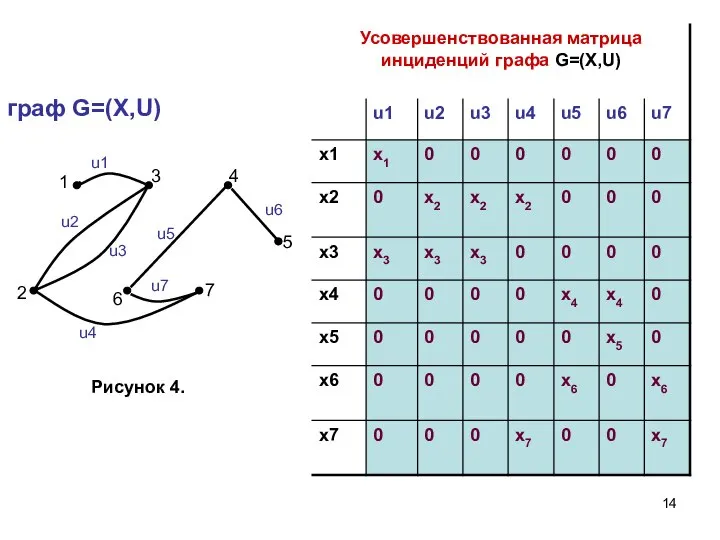
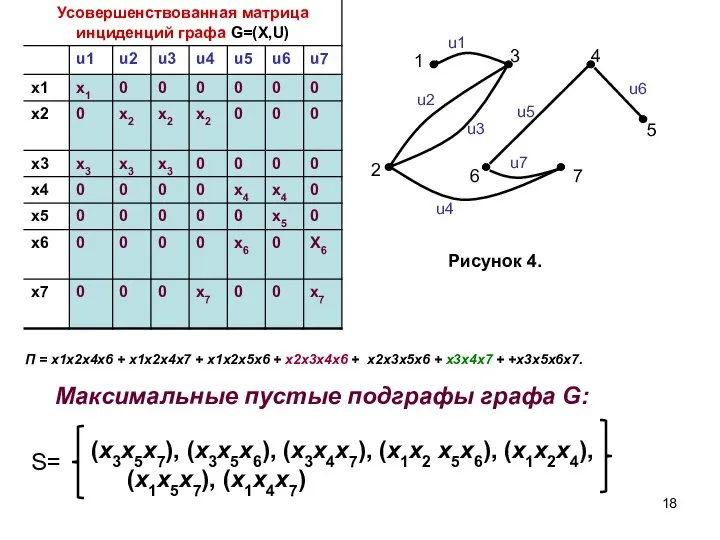
- 13. Усовершенствованная матрица инциденций графа G=(X, U). Для её получения вводится система «псевдобулевских» переменных {xi}, где i
- 14. граф G=(X,U)
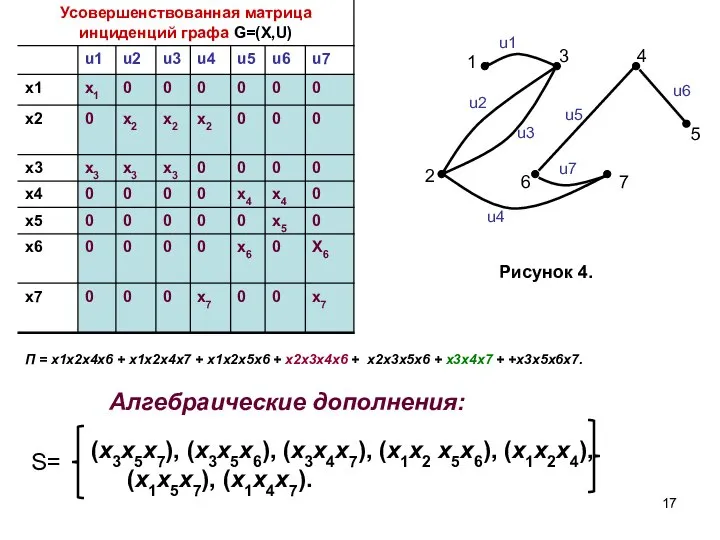
- 15. Составим произведение П: ПG = (x1 + x3) (x2 + x3) (x2 + x3) (x2 +
- 16. Получили произведение П: ПG = x1x2x4x6 + x1x2x4x7 + x1x2x5x6 + x2x3x4x6 + x2x3x5x6 + +
- 17. S= (x3x5x7), (x3x5x6), (x3x4x7), (x1x2 x5x6), (x1x2x4), (x1x5x7), (x1x4x7). Алгебраические дополнения: П = x1x2x4x6 + x1x2x4x7
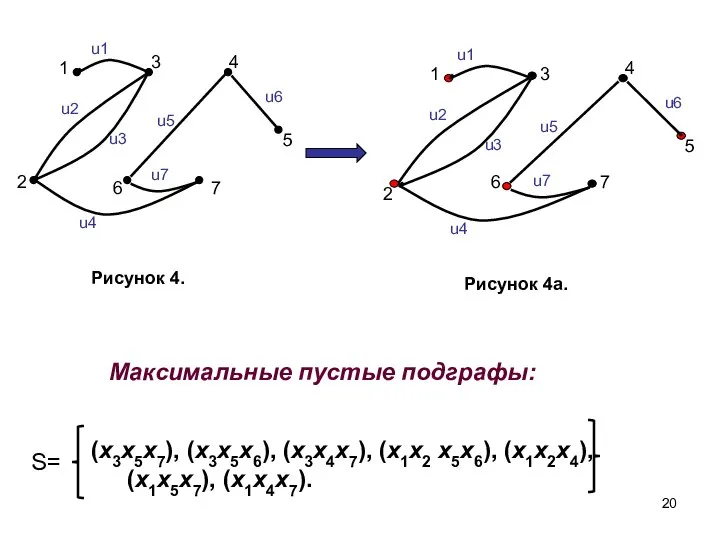
- 18. S= (x3x5x7), (x3x5x6), (x3x4x7), (x1x2 x5x6), (x1x2x4), (x1x5x7), (x1x4x7) Максимальные пустые подграфы графа G: П =
- 19. Раскраска графа Правильная раскраска вершин графа Хроматическое число графа Хроматическое число графа — минимальное количество цветов,
- 20. Максимальные пустые подграфы: 5
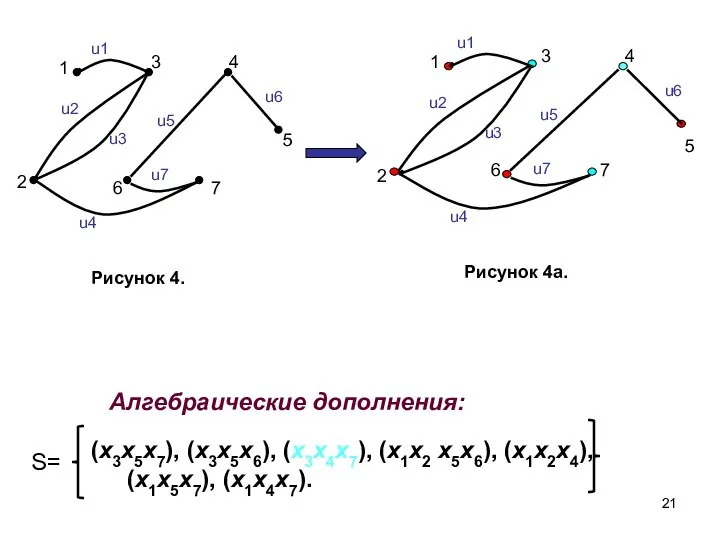
- 21. Алгебраические дополнения: 5
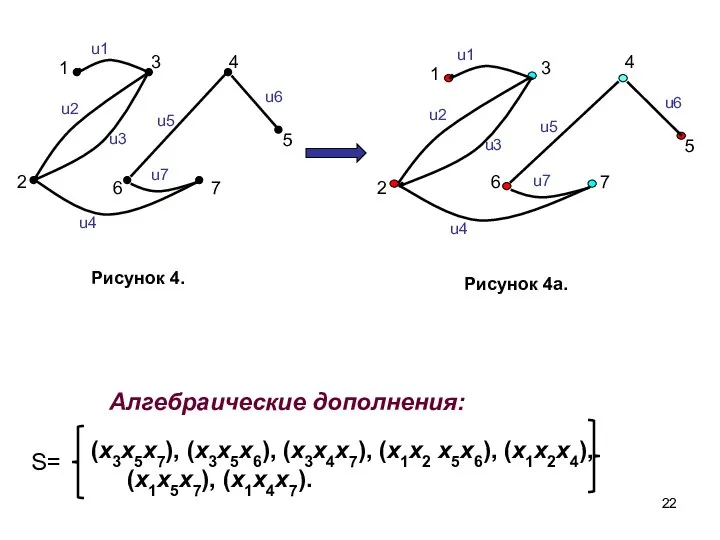
- 22. Алгебраические дополнения: 5
- 23. Максимальные полные подграфы
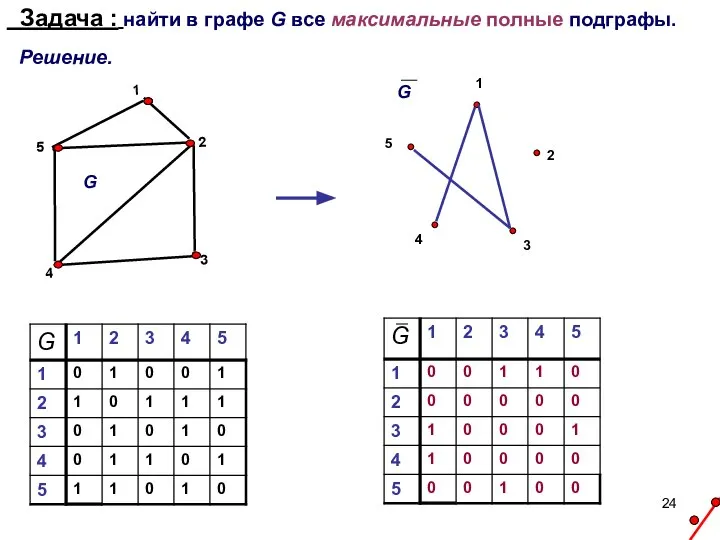
- 24. Задача : найти в графе G все максимальные полные подграфы. Решение.
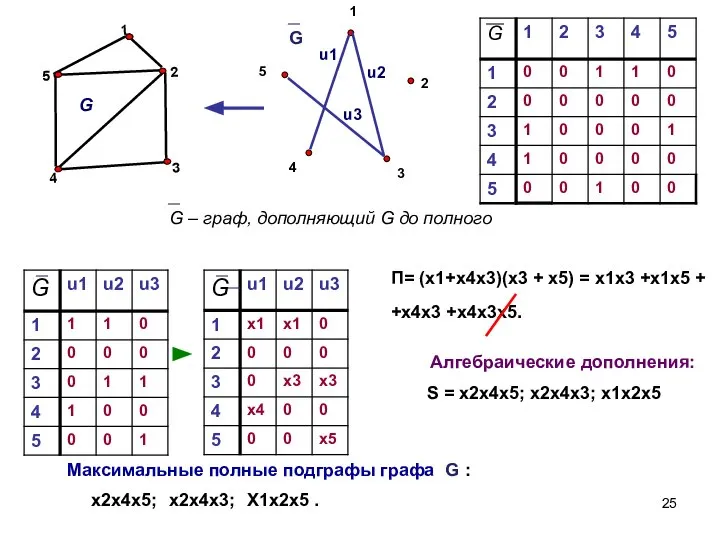
- 25. П= (x1+x4x3)(x3 + x5) = x1x3 +x1x5 + +x4x3 +x4x3x5. Алгебраические дополнения: S = x2x4x5; x2x4x3;
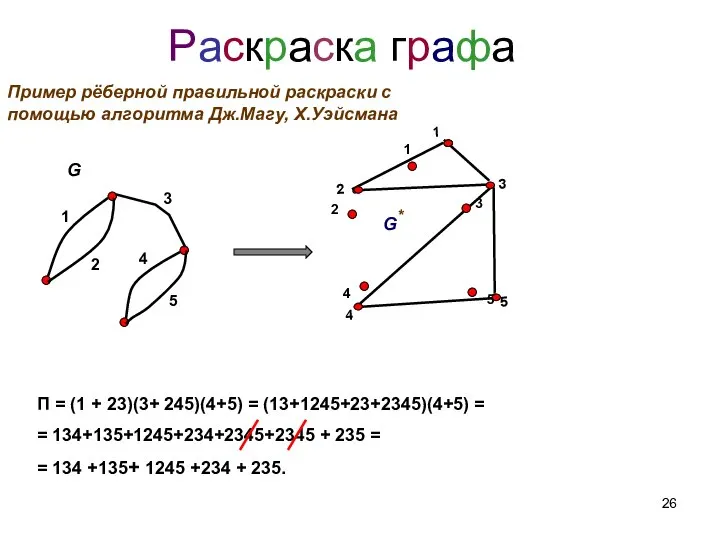
- 26. Раскраска графа Пример рёберной правильной раскраски с помощью алгоритма Дж.Магу, Х.Уэйсмана П = (1 + 23)(3+
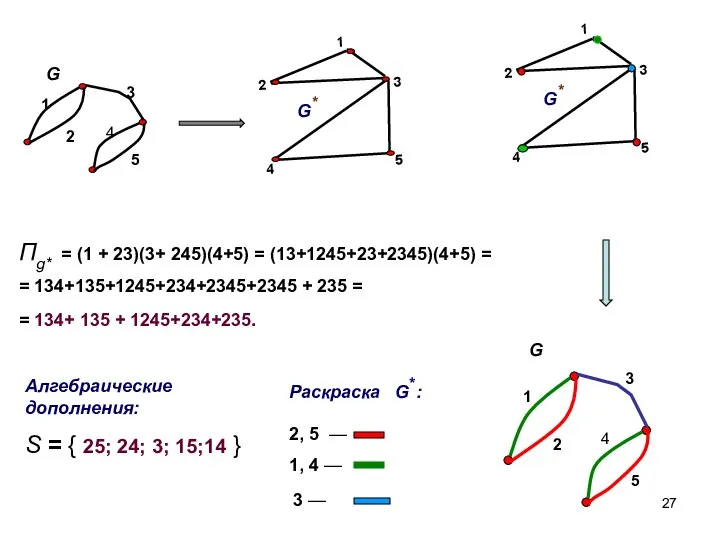
- 27. Пg* = (1 + 23)(3+ 245)(4+5) = (13+1245+23+2345)(4+5) = = 134+135+1245+234+2345+2345 + 235 = = 134+
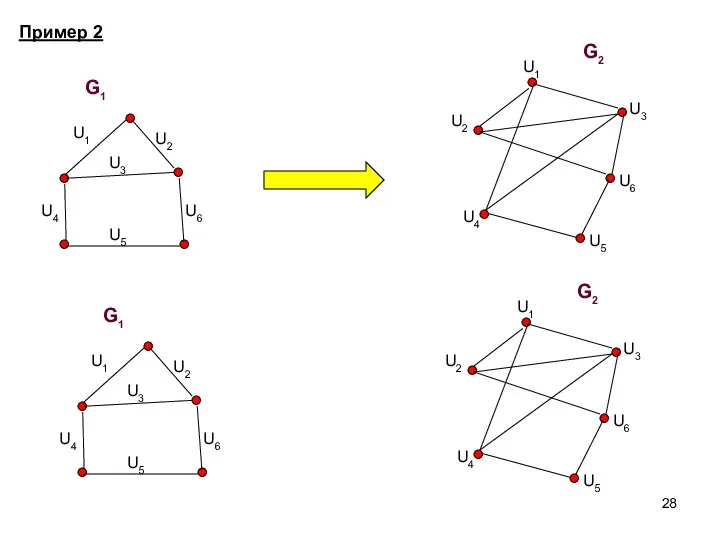
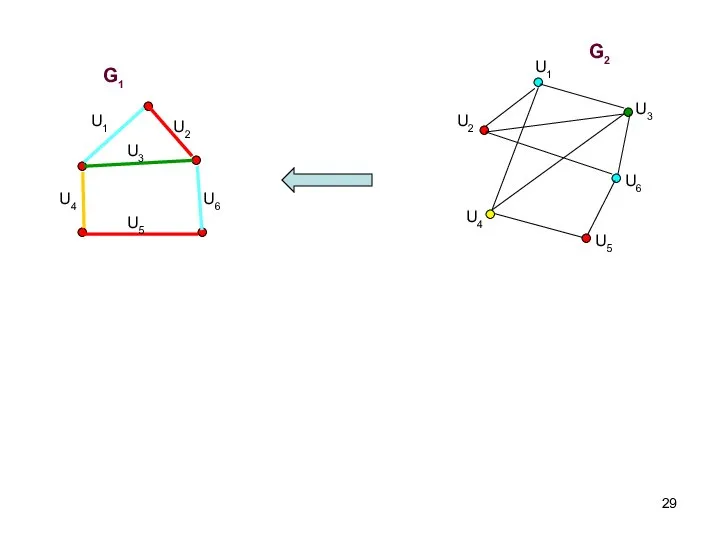
- 28. Пример 2
- 32. Скачать презентацию











 Организация обучения по математике. Принципы отбора содержания и составления дистанционного урока
Организация обучения по математике. Принципы отбора содержания и составления дистанционного урока Сложение чисел с разными знаками 6 класс Выполнила учитель математики ТМБОУ «Дудинская средняя школа №7» Филатова Е.А.
Сложение чисел с разными знаками 6 класс Выполнила учитель математики ТМБОУ «Дудинская средняя школа №7» Филатова Е.А.  Презентация по математике Действия с десятичными дробями
Презентация по математике Действия с десятичными дробями  Синус и тангенс
Синус и тангенс Задачи на разрезание и перекраивание фигур. Урок геометрии для 5 класса
Задачи на разрезание и перекраивание фигур. Урок геометрии для 5 класса Ешение систем линейных уравнений методом крамера
Ешение систем линейных уравнений методом крамера Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Взаимосвязь математики и окружающего мира в симметрии
Взаимосвязь математики и окружающего мира в симметрии События
События Осевая и центральная симметрии
Осевая и центральная симметрии Геометрическая прогрессия
Геометрическая прогрессия Активные методы и технологии обучения математике в начальной школе
Активные методы и технологии обучения математике в начальной школе Презентация по математике "Упрощение выражений" - скачать бесплатно
Презентация по математике "Упрощение выражений" - скачать бесплатно Задания командам. Треугольники. (7 класс)
Задания командам. Треугольники. (7 класс) Геометрические образы, автоматных отображений
Геометрические образы, автоматных отображений Методология математического моделирования
Методология математического моделирования Приведение подобных слагаемых
Приведение подобных слагаемых Числовые выражения
Числовые выражения Координаты вектора
Координаты вектора Закрепление знаний по теме устный счёт
Закрепление знаний по теме устный счёт Математическая логика и теория алгоритмов
Математическая логика и теория алгоритмов Знаки синуса, косинуса, тангенса и котангенса
Знаки синуса, косинуса, тангенса и котангенса Корреляция. Причинность. Детерминизм
Корреляция. Причинность. Детерминизм Поверхности второго порядка
Поверхности второго порядка Женщины в математике
Женщины в математике Алгебраические преобразования с параметрами Изучение многих физических процессов и геометрических закономерностей часто приво
Алгебраические преобразования с параметрами Изучение многих физических процессов и геометрических закономерностей часто приво