Содержание
- 2. В современном мире автоматизации производства теория вероятности(Т.В) необходима специалистам для решения задач, связанных с выявлением возможного
- 3. Под случайным событием понимается всякое явление, о котором имеет смысл говорить, что оно происходит или не
- 4. Основные понятия и термины ТВ Наблюдения, опыты и измерения Испытание - осуществление каждого отдельного наблюдения, опыта
- 5. Основные понятия и термины ТВ Результат испытания называется событием Событие - любой факт, который может произойти
- 6. Основные понятия и термины ТВ Каждое событие обладает объективной возможностью наступления
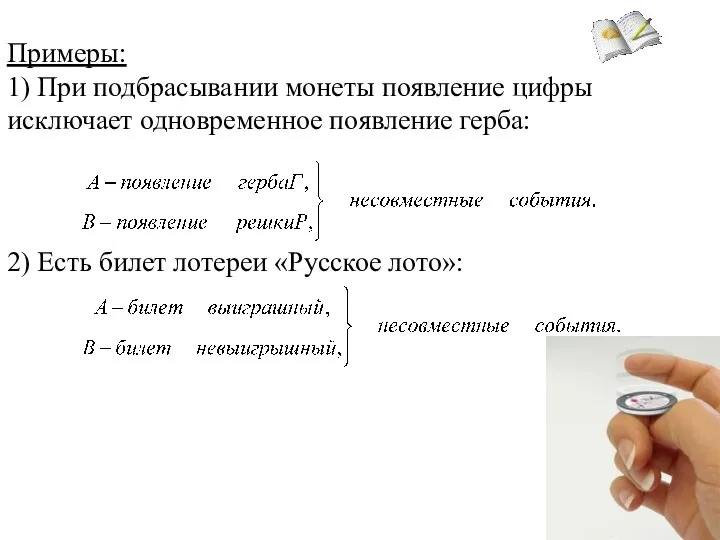
- 8. Примеры: 1) При подбрасывании монеты появление цифры исключает одновременное появление герба: 2) Есть билет лотереи «Русское
- 9. Основные понятия и термины ТВ В любом опыте имеется определенное множество возможных исходов ωi, (i =
- 10. Основные понятия и термины ТВ Например, - пространство элем. исходов опыта, связанного с подбрасыванием одной монеты;
- 11. Основные понятия и термины ТВ Событие - подпространство пространства Событие - подпространство пространства
- 14. Виды событий в ТВ В зависимости от объективной возможности наступления: 1. Достоверное 2. Невозможное 2. Случайное
- 15. Виды случайных событий 1. Простое - не может быть разложено на составляющие. Например: Событие - при
- 16. 2. Сложное (составное) событие - описывается несколькими простыми событиями. Например: событие - при бросании игральной кости
- 17. Виды сложных событий а) Логическая сумма (объединение) простых событий – сложное событие, которое заключается в наступлении
- 18. Виды сложных событий Общепринятая запись суммы (объединения) двух событий: или что означает: - символ логического сложения.
- 19. Сумма (объединение) трех событий: или , что означает: Виды сложных событий
- 20. б) Логическое произведение (пересечение) простых событий - сложное событие, которое заключается в совместном наступлении одновременно или
- 21. Виды сложных событий Например, событие - при бросании двух игральных костей. Или событие
- 22. Общепринятая запись произведения (пересечения): или , что означает: ; - символ логического умножения. Виды сложных событий
- 23. 3. Равновозможные события – имеют одинаковую объективную возможность наступления при данном комплексе условий. Например, события: Виды
- 24. События Виды случайных событий
- 25. События и , где - случ. ошибка измерений, - равновозможны при однократном измерении некоторой величины. Виды
- 26. 4. Единственно возможные события – такие, когда в результате испытания может произойти одно и только одно
- 27. Виды случайных событий 5. Независимые и зависимые события – такие, у которых объективная возможность появления не
- 28. Виды случайных событий Система единственно возможных несовместных событий называется полной группой событий. Так события и при
- 29. Виды случайных событий 6. Противоположные события – два простых или сложных события, образующих полную группу. Событие,
- 30. Виды случайных событий Так, противоположны события: и ; и ; и
- 31. Конечное число несовместных равновозможных событий, образующих полную группу, называются случаями, шансами, элементарными исходами опыта. Например, при
- 32. Про опыт говорят, что он сводится или не сводится к схеме случаев (шансов, элементарных исходов). Элементарный
- 33. Например, в опыте выпадению герба благоприятствует один исход (Г); В опыте выпадению хотя бы одного герба
- 34. Численная мера объективной возможности появления события называется вероятностью события. Вероятность – важнейшая характеристика случайного события. Существует
- 35. Классическое определение вероятности Оно не связано с проведением опытов, т.е. вероятность события определяется исходя лишь из
- 36. Классическое определение вероятности Тогда вероятность события может быть получена по формуле где N – общее число
- 37. Классическое определение вероятности Согласно формулы ( I ), При одном бросании монеты: Р(Г) = 1/2. При
- 38. Классическое определение вероятности В формуле (I) или , т.е. Т.о. предельное числовое значение вероятности вообще есть
- 39. Классическое определение вероятности При имеем - вероятность достоверного события равна единице. При имеем - вероятность невозможного
- 40. Классическое определение вероятности Обозначим и , Тогда , т.к. , т.е. сумма вероятностей противоположных событий равна
- 41. Классическое определение вероятности Недостаток: опыты редко сводятся к схеме случаев и чаще всего нарушается требование равновозможности
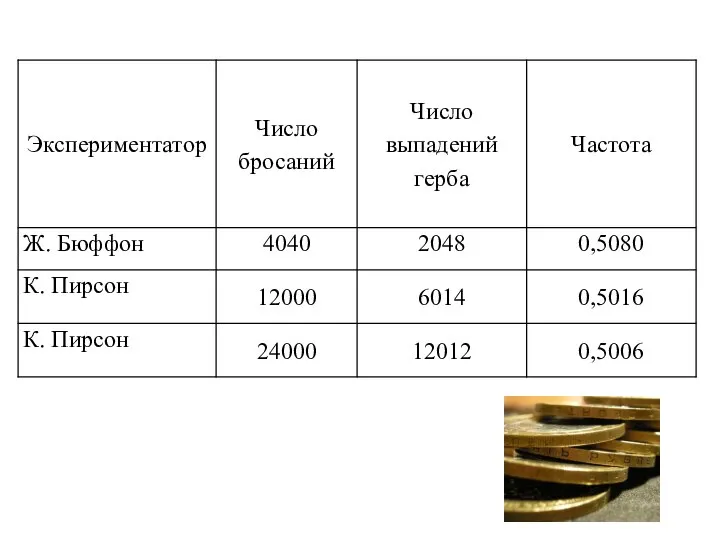
- 42. Статистическое определение вероятности Связано с проведением опытов и с понятием относительной частоты Q – частости- появления
- 43. Статистическое определение вероятности Свойство устойчивости относительной частоты в опытах отражено в теореме Бернулли: где ε и
- 44. На основании теоремы Бернулли : вероятность – это предел, к которому стремится относительная частота Q события
- 45. Практически статистическая вероятность может быть найдена по приближенной формуле (II) Статистическое определение вероятности
- 46. Недостаток - необходимость выполнения бесконечного числа опытов или достаточно большого их числа, что не всегда возможно,
- 47. Формулы ( I ) и ( II ) выражают прямые способы определения вероятностей случайных событий. Они
- 48. Косвенные способы вычисления вероятностей Позволяют по известным вероятностям одних событий вычислять вероятности других, с ними связанных.
- 49. К ним относятся: - теоремы (аксиомы) ТВ; - формула полной вероятности; - формула Байеса; - формула
- 50. Задачи по теме: «Вероятность. Понятие события и вероятности события»
- 51. 1. В урне 3 белых и 9 черных шаров. Из урны наугад вынимается 1 шар. Какова
- 52. 2. Брошена игральная кость. Какова вероятность событий: А- выпало 1 очко; В- выпало 2 очка? Решение:
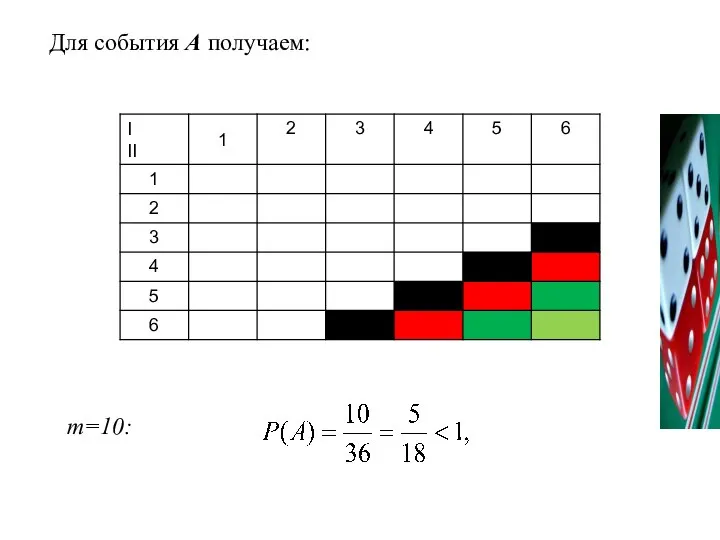
- 53. 3. Брошены 2 игральные кости. Какова вероятность событий: А- выпадения в сумме не менее 9 очков;
- 54. Для события А получаем: m=10:
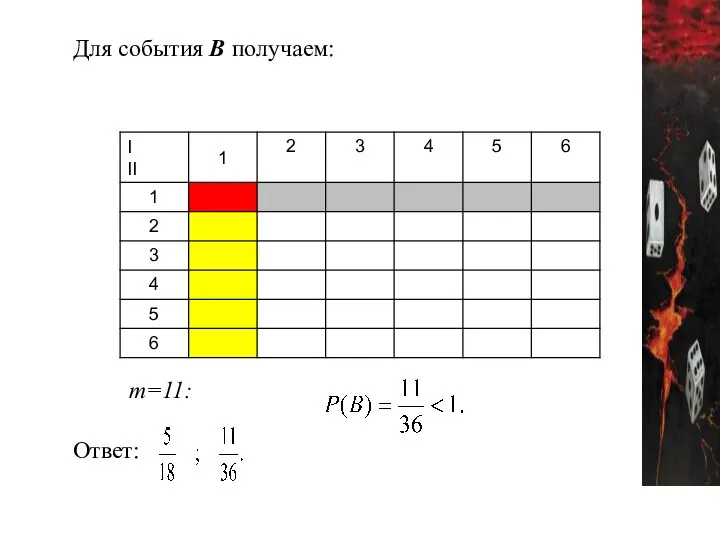
- 55. Для события В получаем: m=11: Ответ:
- 56. Основные теоремы ТВ Используются для вычисления вероятностей сложных событий. Их две – теорема сложения вероятностей и
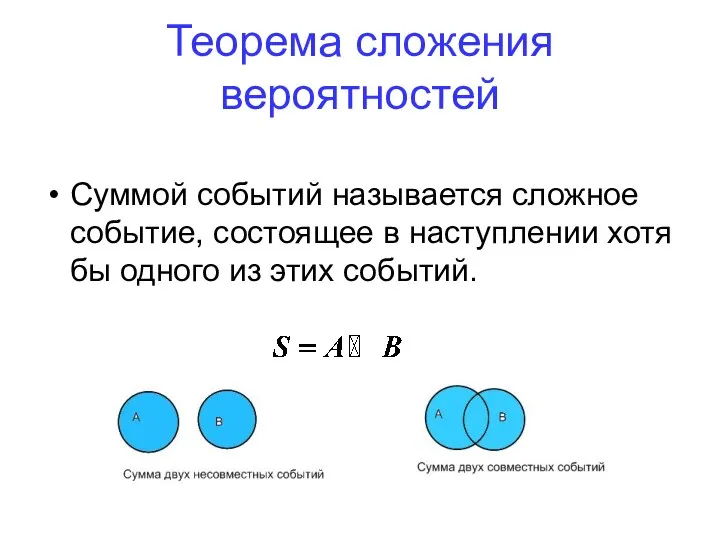
- 57. Теорема сложения вероятностей Суммой событий называется сложное событие, состоящее в наступлении хотя бы одного из этих
- 58. Теорема: Вероятность суммы двух или нескольких совместных событий равна сумме вероятностей этих событий без вероятности их
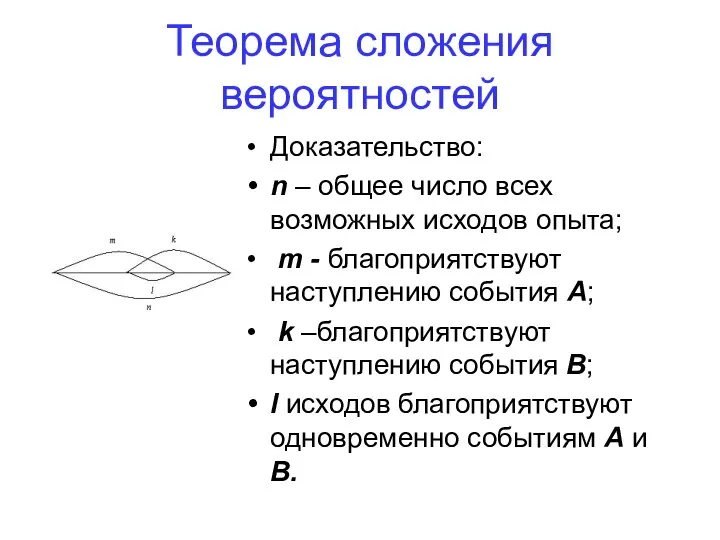
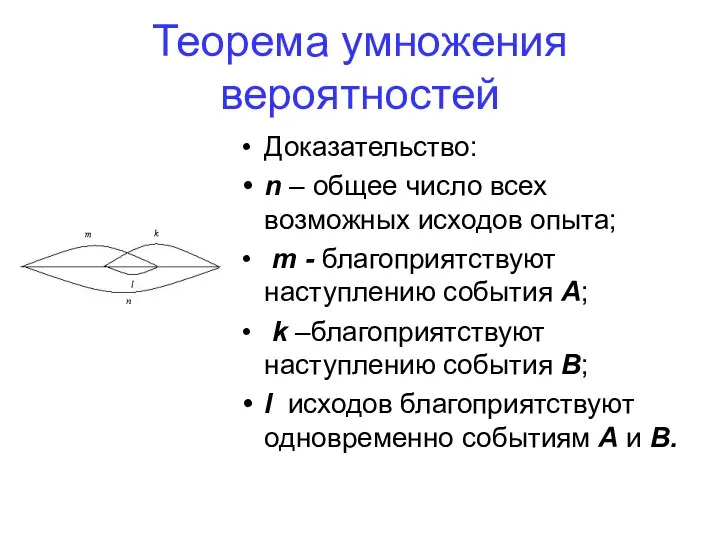
- 59. Теорема сложения вероятностей Доказательство: n – общее число всех возможных исходов опыта; m - благоприятствуют наступлению
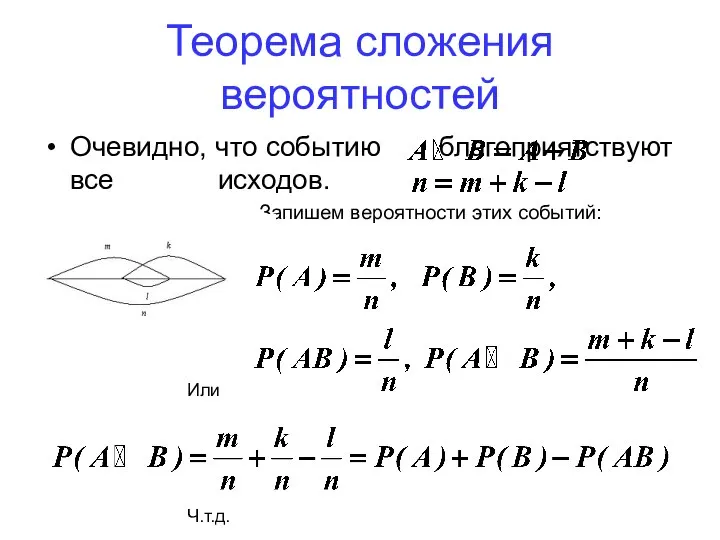
- 60. Очевидно, что событию благоприятствуют все исходов. Запишем вероятности этих событий: Или Ч.т.д. Теорема сложения вероятностей
- 61. Теорема сложения вероятностей Для несовместных событий l = 0. В этом случае т.е. вероятность суммы несовместных
- 62. Задача 1. В лотерее 1000 билетов. На один билет падает выигрыш в 500 рублей, на 10
- 63. Решение: Обозначим события: Найдем вероятности этих простых событий по формуле : Теорема сложения вероятностей
- 64. Теорема сложения вероятностей
- 65. Введем обозначения для интересующих нас событий: - сумма 3-х несовместных событий; - сумма 4-х несовместных событий.
- 66. Вычислим вероятности этих событий по тереме сложения вероятностей несовместных событий: Теорема сложения вероятностей
- 67. Условие независимости событий Два события называются независимыми, если вероятность появления одного из них не зависит от
- 68. Вероятность события, вычисленная в предположении, что одно или несколько событий к этому моменту уже произошли, называется
- 69. События А и В независимы, если их условные вероятности равны “безусловным”,т.е. тот факт, что событие В
- 70. Условие независимости событий Аналитическая запись условия независимости событий: или
- 71. Условная вероятность события может быть получена по формуле Ясно, что если событие А не зависит от
- 72. Задача . Из колоды карт в 36 листов берут наугад одну карту. Рассмотреть события: Определить их
- 73. Решение. Вычислим “безусловные” вероятности событий: Вычислим необходимые условные вероятности: Условие независимости событий
- 74. Выводы: 1. , следовательно, события А и В независимы. 2. , следовательно, события А и С
- 75. Задача . Зависимы или нет противоположные события? Решение. Запишем условие независимости для противоположных событий: А -
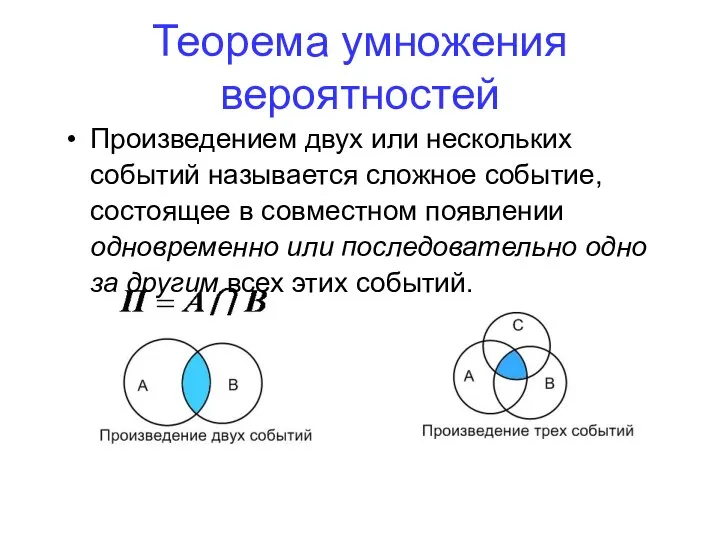
- 76. Теорема умножения вероятностей Произведением двух или нескольких событий называется сложное событие, состоящее в совместном появлении одновременно
- 77. Теорема. Вероятность произведения двух зависимых событий равна произведению безусловной вероятности одного из них на условную вероятность
- 78. Теорема умножения вероятностей Доказательство: n – общее число всех возможных исходов опыта; m - благоприятствуют наступлению
- 79. Теорема умножения вероятностей Запишем вероятности этих событий: Условная вероятность события В: Подставив все эти вероятности в
- 80. Аналогично для трех и более событий: а) б) Для независимых событий А и В: - по
- 81. Теорема умножения вероятностей Задача. На карточках написаны буквы Т, Т, С и О. Карточки перемешаны и
- 82. Теорема умножения вероятностей Решение. Событие по определению есть произведение событий. Вскрытые карточки обратно не возвращаются, поэтому
- 83. Теорема умножения вероятностей (Т, Т, С , О) Поэтому для решения задачи применим теорему умножения вероятностей
- 84. Является следствием обеих теорем – сложения и умножения вероятностей. Формула полной вероятности
- 85. Формула полной вероятности Пусть требуется определить вероятность события А, которое может произойти вместе с одним из
- 86. Формула полной вероятности А – событие H1, H2,…, Hn гипотезы
- 87. Формула полной вероятности Тогда вероятность события А вычисляется как т.е.как сумма произведений вероятности каждой гипотезы на
- 88. Формула полной вероятности Доказательство. Так как гипотезы образуют полную группу, то событие А может появиться только
- 89. Формула полной вероятности Так как гипотезы несовместны, то и комбинации - тоже несовместны Тогда по теореме
- 90. Формула полной вероятности Применяя к событиям теорему умножения зависимых событий, получим , что и требовалось доказать.
- 91. Формула полной вероятности Задача. Имеются три одинаковые с виду урны. В первой - а белых и
- 92. Формула полной вероятности Решение. Событие Обозначим события-гипотезы: 1-я урна 2-я урна 3-я урна H1 H2 H3
- 93. Формула полной вероятности Найдем вероятность вынуть белый шар из 1-й урны, т.е. затем – из 2-й:
- 94. Формула полной вероятности По формуле полной вероятности найдем
- 95. Формула Байеса (теорема гипотез) Является следствием теоремы умножения вероятностей и формулы полной вероятности.
- 96. Формула Байеса (теорема гипотез) Пусть имеется полная группа несовместных гипотез: H1, H2,…, Hn Пусть вероятности этих
- 97. Формула Байеса (теорема гипотез) Вопрос: как следует изменить вероятности гипотез в связи с наступлением этого события?
- 98. Формула Байеса (теорема гипотез) По теореме умножения вероятностей имеем: или , откуда
- 99. Формула Байеса (теорема гипотез) Выражая P(A) с помощью формулы полной вероятности, имеем Формула Байеса дает возможность
- 100. Формула Байеса (теорема гипотез) Задача. Два стрелка стреляют в одну мишень, делая каждый по одному выстрелу.
- 101. Формула Байеса (теорема гипотез) Решение. p1 = 0.8, p2 = 0.4 До опыта возможны следующие гипотезы:
- 102. Формула Байеса (теорема гипотез) Условные вероятности наблюденного события А = {пробоина} при этих гипотезах равны:
- 103. Формула Байеса (теорема гипотез) После опыта гипотезы H 1 и Н 2 становятся невозможными. Вероятности гипотез
- 104. Формула Байеса (теорема гипотез) Следовательно, вероятность того, что пробоина принадлежит первому стрелку, равна .
- 106. Скачать презентацию





























































































 Геометрический материал
Геометрический материал Презентация по математике "Обобщающий урок по теме «Четырехугольники»" - скачать
Презентация по математике "Обобщающий урок по теме «Четырехугольники»" - скачать  Десятичная система счисления
Десятичная система счисления Принятие решений при неполной информации
Принятие решений при неполной информации Математический парадокс Рассела
Математический парадокс Рассела Числовые множества. Признаки делимости
Числовые множества. Признаки делимости Вероятность, комбинаторика в ЕГЭ
Вероятность, комбинаторика в ЕГЭ Наближення функцій
Наближення функцій Тест по геометрии
Тест по геометрии Деление дробей
Деление дробей Геометрическое решение задачи о расстояниях между точками
Геометрическое решение задачи о расстояниях между точками Производная сложной функции. Производная обратной функции. Производная функции, заданной неявно. Теорема. (Семинар 8)
Производная сложной функции. Производная обратной функции. Производная функции, заданной неявно. Теорема. (Семинар 8) Ортогональне проектування
Ортогональне проектування Приведение дробей к новому знаменателю
Приведение дробей к новому знаменателю Аттестационная работа. Планирование работы образовательного учреждения при обучении дисциплин естественно-математического цикл
Аттестационная работа. Планирование работы образовательного учреждения при обучении дисциплин естественно-математического цикл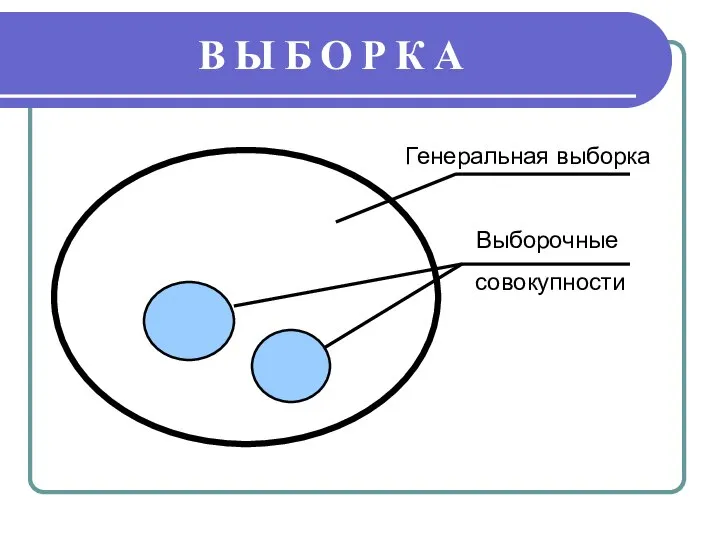 Выборка. Генеральная выборка. Выборочные совокупности
Выборка. Генеральная выборка. Выборочные совокупности Презентация по математике "ПОВТОРЕНИЕ 2 КЛАСС" - скачать бесплатно
Презентация по математике "ПОВТОРЕНИЕ 2 КЛАСС" - скачать бесплатно Тригонометриялық теңдеулерді шешудің тәсілдірі
Тригонометриялық теңдеулерді шешудің тәсілдірі Освобождение от иррациональности в знаменателе дроби
Освобождение от иррациональности в знаменателе дроби Измерение отрезков
Измерение отрезков Однородная система линейных алгебраических уравнений. Фундаментальная система решений
Однородная система линейных алгебраических уравнений. Фундаментальная система решений Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Логарифмическая функция
Логарифмическая функция Основные понятия теории чисел. Лекция 9
Основные понятия теории чисел. Лекция 9 Принцип Дирихле
Принцип Дирихле Теория графов
Теория графов Свойства степени с натуральным показателем. 7 класс
Свойства степени с натуральным показателем. 7 класс Презентация ученицы 549 школы 6 класса «А» Симоновой Наташи
Презентация ученицы 549 школы 6 класса «А» Симоновой Наташи