Содержание
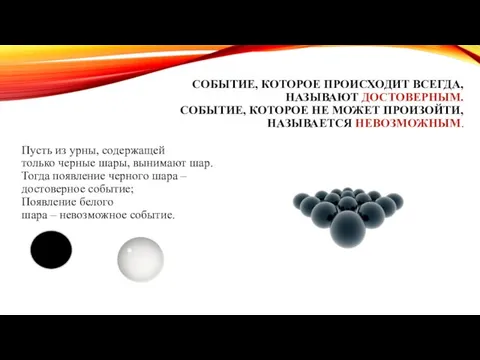
- 2. СОБЫТИЕ, КОТОРОЕ ПРОИСХОДИТ ВСЕГДА, НАЗЫВАЮТ ДОСТОВЕРНЫМ. СОБЫТИЕ, КОТОРОЕ НЕ МОЖЕТ ПРОИЗОЙТИ, НАЗЫВАЕТСЯ НЕВОЗМОЖНЫМ. Пусть из урны,
- 3. ДВА СОБЫТИЯ, КОТОРЫЕ В ДАННЫХ УСЛОВИЯХ МОГУТ ПРОИСХОДИТЬ ОДНОВРЕМЕННО, НАЗЫВАЮТСЯ СОВМЕСТНЫМИ, А ТЕ, КОТОРЫЕ НЕ МОГУТ
- 4. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ. Вероятностью P события А при проведении некоторого испытания называют отношение числа тех исходов,
- 5. АЛГОРИТМ НАХОЖДЕНИЯ ВЕРОЯТНОСТИ СЛУЧАЙНОГО СОБЫТИЯ Для нахождения вероятности случайного события А при проведении некоторого испытания следует
- 6. Из карточек составили слово «пирамида». Какую карточку с буквой вероятнее всего вытащить? Какие события равновероятные? Всего
- 7. СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ В решениях задач этого блока используются следующие утверждения из теории вероятности. Вероятность
- 8. ТИПЫ ЗАДАЧ НА ОГЭ 1. Простые задачи на классическое определение вероятности А)Задачи на брак, неисправность, выученный
- 9. На 100 электрических лампочек в среднем приходится 25 бракованных. Какова вероятность купить исправную лампочку? Опыт имеет
- 10. В коробке лежат 5 красных, 7 зеленых и 2 синих кубика. Случайным образом из коробки берут
- 11. В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22 из США, остальные — из
- 12. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
- 13. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9? Решение
- 14. Известно, что в некотором регионе вероятность того, что родившийся младенец окажется мальчиком, равна 0,512. В 2010
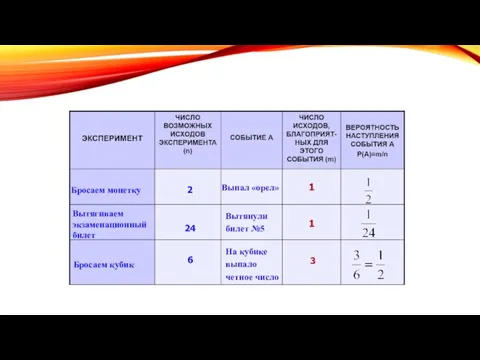
- 15. Бросаем монетку Вытягиваем экзаменационный билет Бросаем кубик 2 24 6 Выпал «орел» Вытянули билет №5 На
- 16. Вероятность того, что новый сканер прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше
- 17. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите
- 19. Скачать презентацию














 Нахождение числа по его дроби. Дробные выражения. 6 класс
Нахождение числа по его дроби. Дробные выражения. 6 класс Бинарные (фиктивные) переменные
Бинарные (фиктивные) переменные Учитель математики МОУ СОШ №9 Левокумского района Перепелицына Людмила Владимировна «Использование информационно-коммуник
Учитель математики МОУ СОШ №9 Левокумского района Перепелицына Людмила Владимировна «Использование информационно-коммуник Правила сравнения чисел
Правила сравнения чисел Введение в метрологию
Введение в метрологию Сапалық белгілерді талдау. Екі тәуелсіз жиынтықтарды салыстыру үшін Z тест: сенім аралықтары әдісі
Сапалық белгілерді талдау. Екі тәуелсіз жиынтықтарды салыстыру үшін Z тест: сенім аралықтары әдісі Призма. Определение призмы
Призма. Определение призмы Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Планирование эксперимента для применения корреляционного анализа. Лекция 4
Планирование эксперимента для применения корреляционного анализа. Лекция 4 Решение уравнений
Решение уравнений Матрицы и определители
Матрицы и определители Первый замечательный предел
Первый замечательный предел Геометрія. Многогранники
Геометрія. Многогранники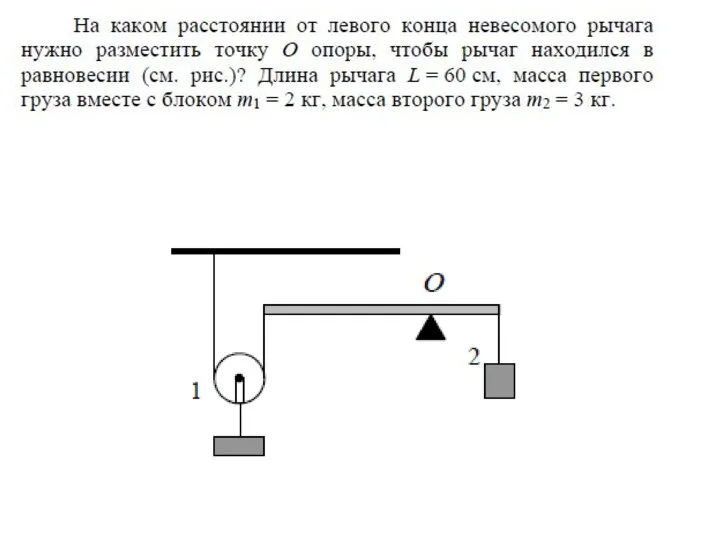 Задачи на расстояние
Задачи на расстояние Формула полной вероятности
Формула полной вероятности Презентация на тему Параллельность прямых
Презентация на тему Параллельность прямых  Тождественные преобразования. 7 класс
Тождественные преобразования. 7 класс Игра Математическое кафе
Игра Математическое кафе Приемы устных вычислений
Приемы устных вычислений Переместительное и сочетательное свойства
Переместительное и сочетательное свойства Решение задач с помощью систем уравнений второй степени
Решение задач с помощью систем уравнений второй степени Логарифмические неравенства
Логарифмические неравенства Оценка точности функций
Оценка точности функций Естественно-математическое ралли!!!!
Естественно-математическое ралли!!!! Прямоугольные треугольники
Прямоугольные треугольники Тест. Площадь многоугольника
Тест. Площадь многоугольника Урок-презентация по теме «Неравенство треугольника» геометрия 7 класс Чечина Ольга Юрьевна учитель математики МБОУ лицей №1 г.
Урок-презентация по теме «Неравенство треугольника» геометрия 7 класс Чечина Ольга Юрьевна учитель математики МБОУ лицей №1 г. Основное свойство дроби Горбунова Александра, ученица 6 класса Руководитель: учитель математики Воронцова Татьяна Ивановн
Основное свойство дроби Горбунова Александра, ученица 6 класса Руководитель: учитель математики Воронцова Татьяна Ивановн