Содержание
- 2. Векторная алгебра Определение Вектором называется направленный отрезок Обозначение вектора: - длина вектора Определение Вектор, длина которого
- 3. Векторная алгебра Определение Единичный вектор, направление которого совпадает с направлением вектора называется ортом вектора и обозначается
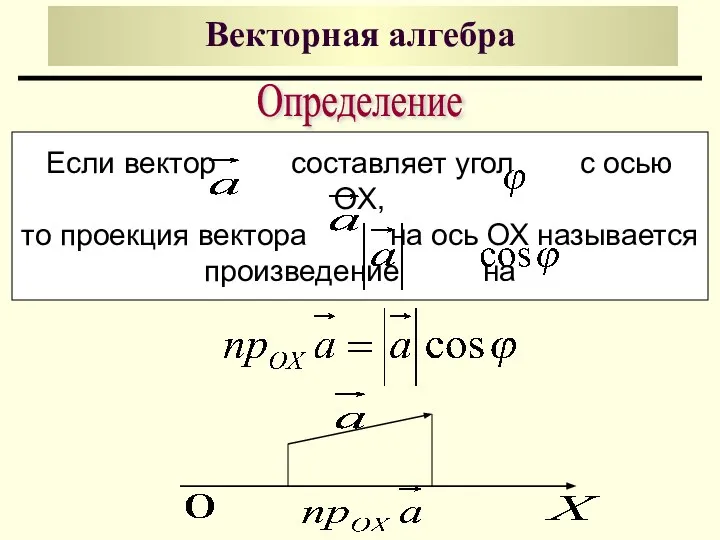
- 4. Векторная алгебра Если вектор составляет угол с осью OX, то проекция вектора на ось ОХ называется
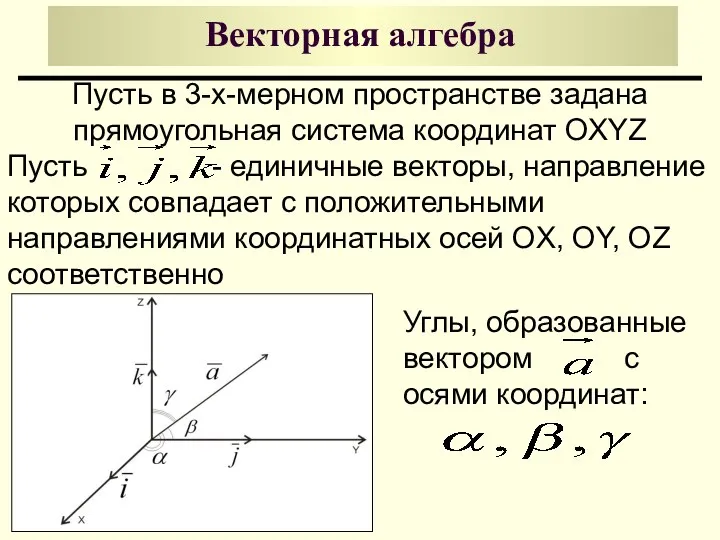
- 5. Векторная алгебра Пусть в 3-х-мерном пространстве задана прямоугольная система координат OXYZ Пусть - единичные векторы, направление
- 6. Векторная алгебра Проекция вектора на оси координат Вектор имеет координаты x, y, z, то есть в
- 7. Действия сложения векторов и умножения вектора на число называются линейными операциями над векторами Векторная алгебра Пусть
- 8. Векторы называются линейно зависимыми, если существуют такие действительные числа одновременно не обращающиеся в ноль , что
- 9. Пример Рассмотрим на плоскости два неколлинеарных вектора и Покажем, что эти векторы линейно независимы (метод от
- 10. Пример Проверим, являются ли линейно зависимыми вектора По определению линейно (не)зависимых векторов Запишем это равенство для
- 11. Пример Получена система линейных однородных уравнений относительно неизвестных . Если ранг матрицы системы меньше 3, то
- 12. Пример Вектора линейно независимые
- 13. Векторная алгебра Пусть - неколлинеарные векторы на плоскости, тогда всякий комплонарный им вектор можно представить и
- 14. Векторная алгебра Доказательство 1) Покажем существование разложения По условию векторы - неколлинеарные векторы эти векторы не
- 15. Векторная алгебра В случае, если тогда разложение (2) справедливо при Одновременное выполнение не может быть
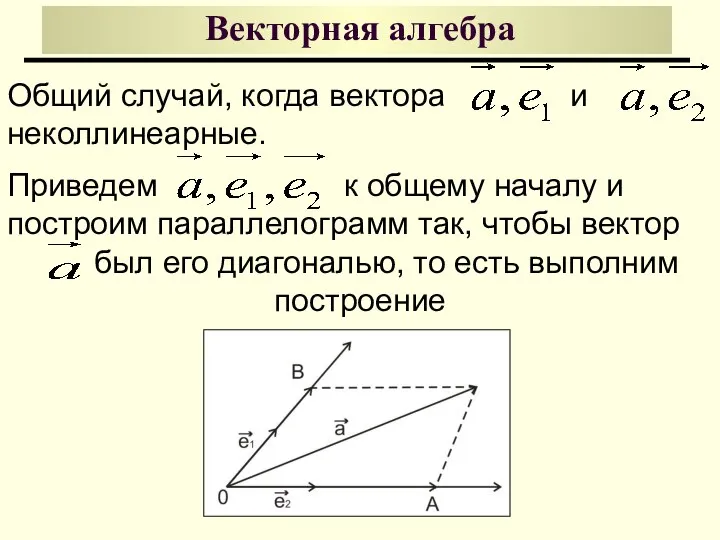
- 16. Векторная алгебра Общий случай, когда вектора и неколлинеарные. Приведем к общему началу и построим параллелограмм так,
- 17. Векторная алгебра По правилу сложению векторов Таким образом, разложение (2) существует
- 18. Векторная алгебра 1) Докажем единственность разложения (2) Предположим противное, что разложение (2) не единственно, то есть
- 19. Векторная алгебра Таким образом, существует такое число что выполняется (*) вектора . коллинеарные, что противоречит условию
- 21. Скачать презентацию















 Моделирование рядов динамики
Моделирование рядов динамики Натуральные и целые числа
Натуральные и целые числа Лесная математика. Русская красавица
Лесная математика. Русская красавица Правило параллелепипеда
Правило параллелепипеда Графическое решение уравнений и неравенств с параметрами
Графическое решение уравнений и неравенств с параметрами Статистика национального богатства
Статистика национального богатства Десятичные и натуральные логарифмы. Формула перехода
Десятичные и натуральные логарифмы. Формула перехода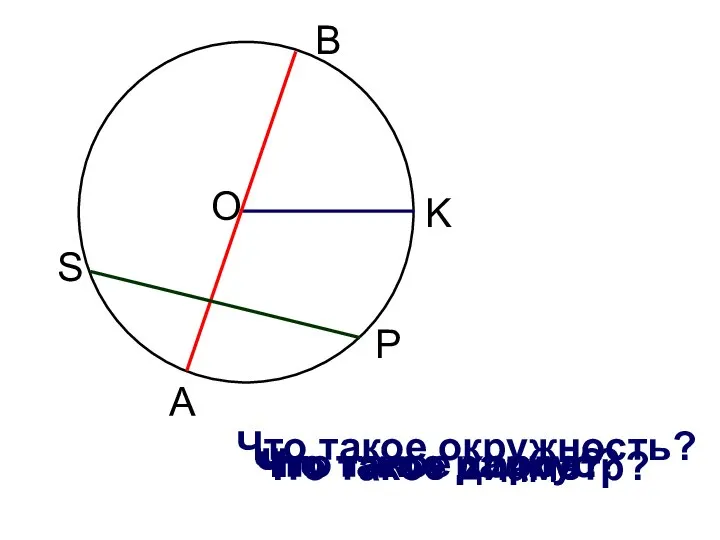 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Вектори у просторі
Вектори у просторі Построение правильных многоугольников
Построение правильных многоугольников Введение в эконометрику
Введение в эконометрику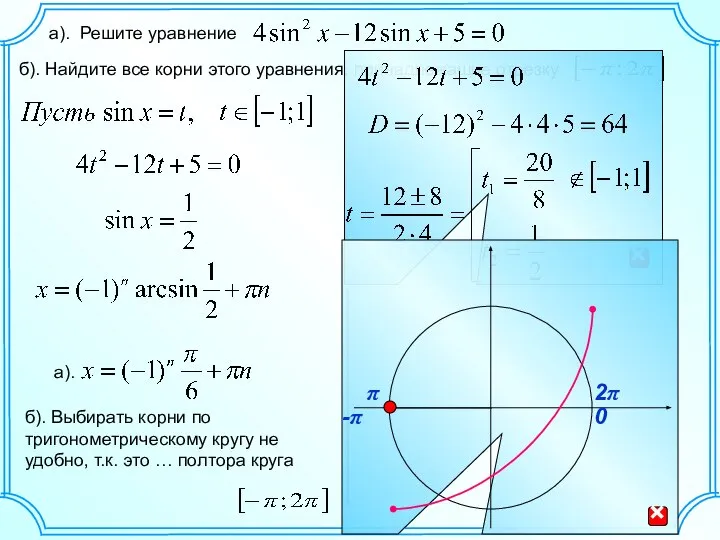 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии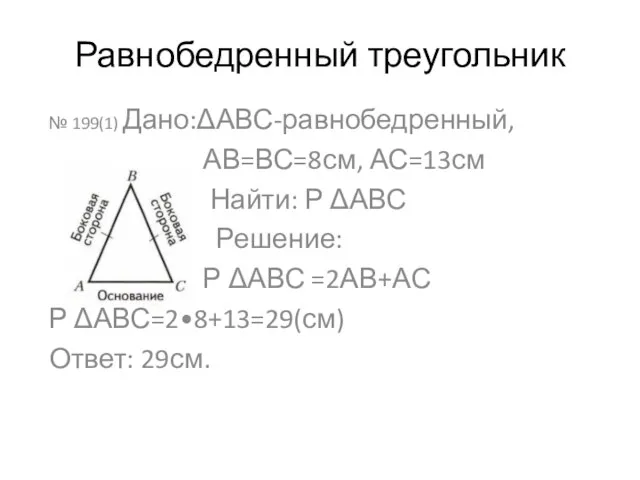 Равнобедренный треугольник
Равнобедренный треугольник Капризная формула. Теорема Эйлера
Капризная формула. Теорема Эйлера Теория поверхностей. Задание поверхности
Теория поверхностей. Задание поверхности Елементи математичної логіки. Висловлювання та операції над ними
Елементи математичної логіки. Висловлювання та операції над ними Наибольший общий делитель
Наибольший общий делитель Функция у=ах2 +bx + c ее свойства и график. 8 класс
Функция у=ах2 +bx + c ее свойства и график. 8 класс Неделя математики. Конкурсы
Неделя математики. Конкурсы Пропорции (11 класс) - презентация_
Пропорции (11 класс) - презентация_ Презентация Логика финансовых вычислений
Презентация Логика финансовых вычислений Основы логики
Основы логики Погрешности измерений
Погрешности измерений Теорема Пифагора. (8 класс)
Теорема Пифагора. (8 класс) Презентация по математике "Устный счет" - скачать
Презентация по математике "Устный счет" - скачать  Základy statistiky
Základy statistiky Дискретная математика. Основные понятия теории множеств. (Лекция 1.1)
Дискретная математика. Основные понятия теории множеств. (Лекция 1.1) Нестандартные способы решения тригонометрических уравнений
Нестандартные способы решения тригонометрических уравнений