Вычисление площадей с помощью интеграла

Июль 23, 2022

Главная
Математика
Вычисление площадей с помощью интеграла

Содержание

2. Определенный интеграл. Ребята, на прошлом уроке мы с вами уже вычисляли площади различных фигур, ограниченных некоторым
3. Определенный интеграл. До сих пор мы вычисляли площади фигур, которые были расположены выше оси абсцисс. Давайте
4. Определенный интеграл. Площадь требуемой фигуры S можно вычислить как разность двух площадей двух фигур: первая фигура
5. Определенный интеграл. Площадь фигуры ограниченной прямыми x=a и x=b и графиками функций y=f(x) и y=g(x), непрерывных
6. Определенный интеграл. Пример. Вычислить площадь фигуры, ограниченной линиями Решение. Построим графики наших функций на одной координатной
7. Определенный интеграл. Пример. Вычислить площадь фигуры, ограниченной линиями Решение. Построим графики наших функций. График первой функции
8. Определенный интеграл. Оба графика построим на одной координатной плоскости Площадь требуемой фигуры закрашена. Давайте вычислим ее.
10. Скачать презентацию

Слайд 2

Определенный интеграл.
Ребята, на прошлом уроке мы с вами уже вычисляли площади

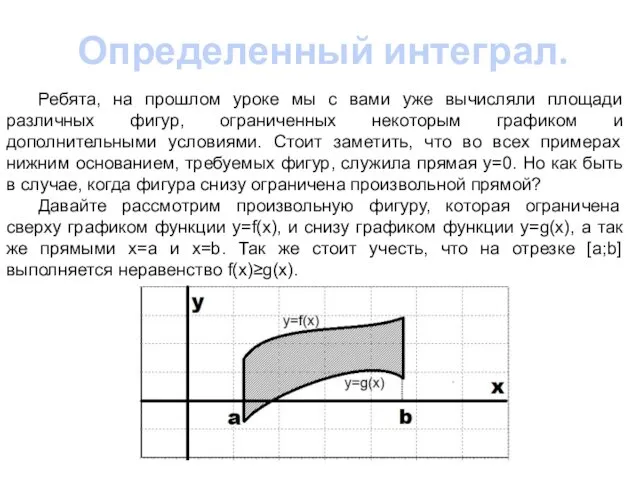
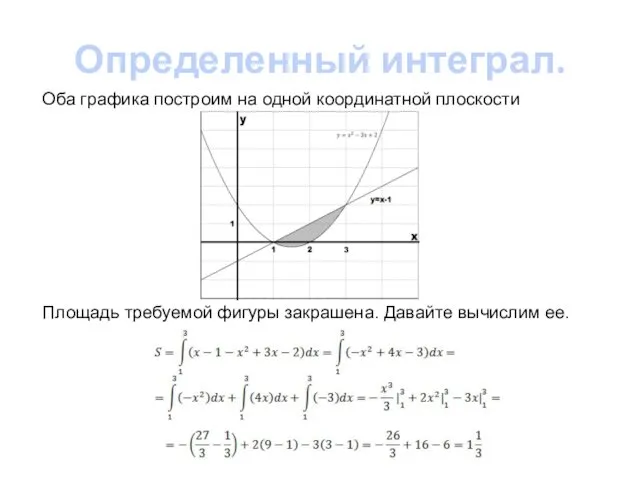
различных фигур, ограниченных некоторым графиком и дополнительными условиями. Стоит заметить, что во всех примерах нижним основанием, требуемых фигур, служила прямая y=0. Но как быть в случае, когда фигура снизу ограничена произвольной прямой?
Давайте рассмотрим произвольную фигуру, которая ограничена сверху графиком функции y=f(x), и снизу графиком функции y=g(x), а так же прямыми x=a и x=b. Так же стоит учесть, что на отрезке [a;b] выполняется неравенство f(x)≥g(x).

Слайд 3

Определенный интеграл.
До сих пор мы вычисляли площади фигур, которые были

расположены выше оси абсцисс. Давайте нашу фигуру параллельно перенесем на m единиц вверх, площадь фигуры от такой операции не изменится, изменится только общий вид заданных функций. Сверху наша фигура будет ограничена функцией y=f(x)+m, снизу не трудно догадаться y=g(x)+m.

Слайд 4

Определенный интеграл.
Площадь требуемой фигуры S можно вычислить как разность двух площадей

двух фигур: первая фигура ограничена прямыми x=a и x=b, осью абсцисс и функцией y=f(x)+m, обозначим как S1. Вторая фигура ограничена прямыми x=a и x=b, осью абсцисс и функцией y=g(x)+m, обозначим как S2. Тогда

Слайд 5

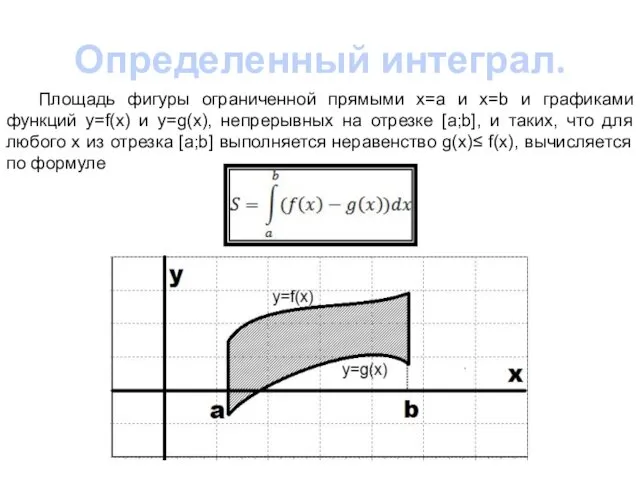
Определенный интеграл.

Площадь фигуры ограниченной прямыми x=a и x=b и

графиками функций y=f(x) и y=g(x), непрерывных на отрезке [a;b], и таких, что для любого х из отрезка [a;b] выполняется неравенство g(x)≤ f(x), вычисляется по формуле

Слайд 6

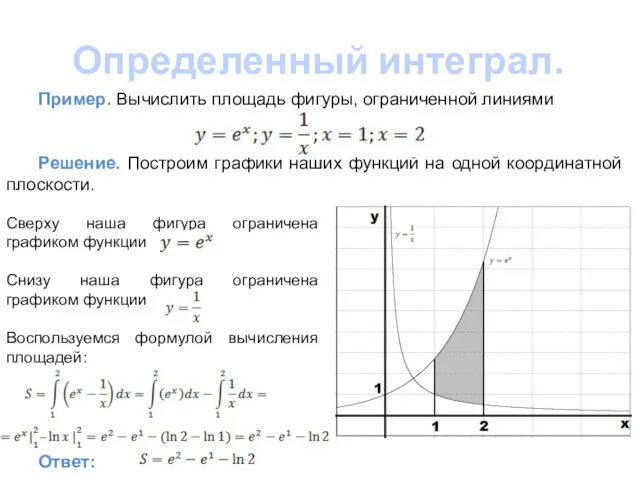
Определенный интеграл.
Пример. Вычислить площадь фигуры, ограниченной линиями
Решение. Построим графики наших функций

на одной координатной плоскости.
Ответ:

Сверху наша фигура ограничена графиком функции
Снизу наша фигура ограничена графиком функции
Воспользуемся формулой вычисления площадей:

Слайд 7

Определенный интеграл.
Пример. Вычислить площадь фигуры, ограниченной линиями
Решение. Построим графики наших функций.
График

первой функции - парабола, ее вершину легко найти, прировняв уравнение производной к нулю
Вычислим значение самой функции в вершине
Дальше график параболы легко построить по точкам.
График второй функции – прямая. Такие графики мы умеем легко строить.

Слайд 8

Определенный интеграл.
Оба графика построим на одной координатной плоскости
Площадь требуемой фигуры

закрашена. Давайте вычислим ее.

Вычисление площадей с помощью интеграла

Содержание

Определенный интеграл. Ребята, на прошлом уроке мы с вами уже вычисляли площади

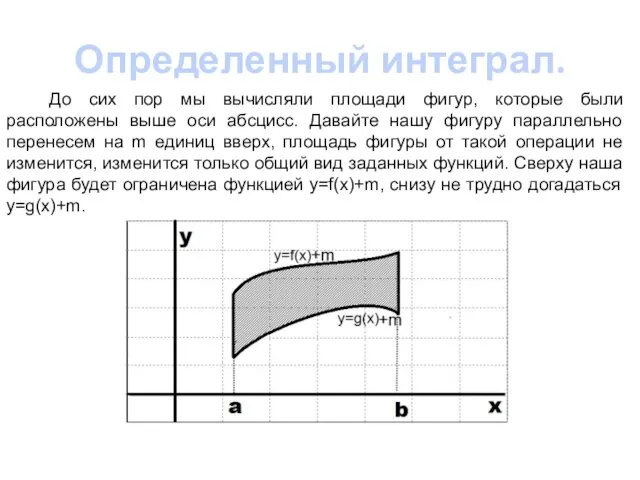
Определенный интеграл. До сих пор мы вычисляли площади фигур, которые были

Определенный интеграл. Площадь требуемой фигуры S можно вычислить как разность двух площадей

Определенный интеграл. Площадь фигуры ограниченной прямыми x=a и x=b и

Определенный интеграл. Пример. Вычислить площадь фигуры, ограниченной линиямиРешение. Построим графики наших функций

Определенный интеграл. Пример. Вычислить площадь фигуры, ограниченной линиямиРешение. Построим графики наших функций.График

Определенный интеграл. Оба графика построим на одной координатной плоскостиПлощадь требуемой фигуры

Похожие презентации